Экспериментальные основы теории
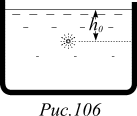 Задача 6. Точечный источник света находится в центре очень широкого сосуда с абсолютно поглощающими стенками на глубине h0, заполненного жидкостью с показателем преломления, плавно увеличивающемся от поверхности вглубь по закону
Задача 6. Точечный источник света находится в центре очень широкого сосуда с абсолютно поглощающими стенками на глубине h0, заполненного жидкостью с показателем преломления, плавно увеличивающемся от поверхности вглубь по закону 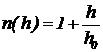 . Мощность излучения источника равна P. Чему равна мощность излучения через свободную поверхность жидкости?
. Мощность излучения источника равна P. Чему равна мощность излучения через свободную поверхность жидкости?
занятие 1.5.1
экспериментальные основы теории
относительности
1. Парадоксы электродинамики
1.1 Сила Лоренца. Взаимодействие движущихся частиц
Рассмотрим некоторые опытные факты из электродинамики, анализ которых заставил физиков пересмотреть принцип относительности Галилея и по-новому взглянуть на пространство и время.
Например, формула для вычисления силы Лоренца 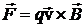 содержит величину
содержит величину ![]() — скорость движения заряженной частицы. Могут возникнуть вопросы: относительно чего определена эта скорость, как пользоваться этой формулой при переходе из одной инерциальной системы отсчета в другую.
— скорость движения заряженной частицы. Могут возникнуть вопросы: относительно чего определена эта скорость, как пользоваться этой формулой при переходе из одной инерциальной системы отсчета в другую.
Или, при изучении электромагнитных волн было установлено, что скорость их распространения равна 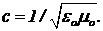 Озадачивает то, что не определена система отсчета, в которой скорость света равна этому значению.
Озадачивает то, что не определена система отсчета, в которой скорость света равна этому значению.
1.1.1 Движение электрона в магнитном поле
Пусть вдоль проводника с током, на некотором расстоянии r от оси в том же направлении, что и электроны проводимости провода, летит электрон. Положим, что скорости наружного электрона и электронов проводимости равны. Полный заряд провода равен нулю, т. к. положительные заряды ионов точно компенсируются зарядами электронов проводимости. Вокруг провода имеется только магнитное поле 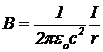 . Движущийся со скоростью v электрон испытывает действие силы Лоренца
. Движущийся со скоростью v электрон испытывает действие силы Лоренца 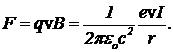 (1)
(1)
Траектория электрона будет загибаться к проводу.
Рассмотрим это же явление из системы отсчета, в которой внешний электрон покоится (мы — наблюдатели — движемся вместе с электроном). В новой системе отсчета электроны проводимости покоятся, зато движутся ионы (т. к. движется назад весь провод). Магнитное поле создается движущимися ионами. С точки зрения наблюдателя, v=0, а поэтому, хоть магнитная индукция осталась прежней, сила Лоренца оказывается равной нулю. Получается, что поведение электрона зависит от наблюдателя. Это абсурдный результат! Все, что происходит в мире, вообще не должно зависеть от того, есть или нет наблюдатели.
Первое рассмотрение подтверждается экспериментом, а второе — нет. Значит, рассмотрение системы электрон-провод с током из движущейсясистемы отсчета чего-то не учитывает, или же закон Ампера нуждается в поправке.
1.1.2 Взаимодействие движущихся частиц
К аналогичному парадоксу приходим при анализе взаимодействия движущихся заряженных частиц. Рассмотрим два электрона, движущихся с равными скоростями v параллельными курсами так, что соединяющая их линия перпендикулярна направлению движения. В курсе 10 класса было установлено, что заряженная частица, движущаяся со скоростью ![]() , создает магнитное поле
, создает магнитное поле ![]()
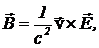 (2)
(2)
где ![]() — напряженность электрического поля, создаваемого частицей в точке наблюдения. Отсюда следует, что каждый из электронов движется в магнитном поле своего соседа. Помимо силы электростатического отталкивания электроны испытывают амперовское притяжение.
— напряженность электрического поля, создаваемого частицей в точке наблюдения. Отсюда следует, что каждый из электронов движется в магнитном поле своего соседа. Помимо силы электростатического отталкивания электроны испытывают амперовское притяжение.
Задача 1. а) Рассчитайте силу Ампера между двумя электронами, находящимися в описанной выше ситуации.
б) Определите, при какой скорости электронов сила Ампера уравновесит кулоновское отталкивание.
Итак, из решения задачи 1 следует, что в зависимости от скорости движения электронов результирующая сила взаимодействия может быть большей или меньшей, или равной нулю, или даже отталкивание смениться притяжением.
Рассмотрим теперь взаимодействие электронов, двигаясь вместе с ними с их скоростью. В новой системе отсчета электроны покоятся и магнитное поле не создают, поэтому, никакой силы Ампера между ними не возникает. Электроны испытывают только электростатическое отталкивание. Снова получается, что поведение электронов зависит от наблюдателя. Опять абсурдный результат! Рассмотрение нуждается в корректировке.
1.2 Ускорители. Недостижимость скорости света
Еще одна головоломка возникает при анализе экспериментов по ускорению заряженных частиц. С помощью электрического поля можно разгонять заряженные частицы до больших скоростей. Если, пульсирующий пучок электронов (поток сгустков электронов) пропустить через два сетчатых электрода, к которым приложена ускоряющая разность потенциалов U, то при прохождении электродов электроны получают приращение кинетической энергии, равное eU. В описываемом опыте свободно движущиеся после прохождения электродов электроны пропускали через две дополнительные металлические сетки. Сетки были подключены к осциллографу с большим временным разрешением. При пролете сгустка сквозь сетку часть электронов оставалась на сетке. Сетка немного подзаряжалась и ее потенциал чуть-чуть изменялся. На экране осциллографа возникал всплеск. То же самое происходило при пролете сгустка сквозь вторую сетку. Всплеск на экране осциллографа происходил немного позднее — через время, необходимое для преодоления сгустком расстояния L между сетками. За это время луч осциллографа успевал сместиться и всплеск оказывался на экране в другом месте. Этот эксперимент позволял по известной частоте развертки осциллографа и взаимному расположению всплесков на экране измерять время пролета сгустком расстояния между сетками. Далее сгустки один за другим попадали в детектор, отдавая ему энергию, от чего он нагревался. Измерение повышения температуры детектора позволяло проконтролировать, не потеряли ли электроны по дороге часть энергии. Опыт показал, что нет — потерь энергии по дороге не происходит.
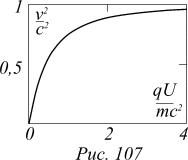 Задача 2. Электроны с пренебрежимо малой начальной скоростью пролетают ускоряющие электроды. Постройте зависимость квадрата скорости пролетевших сквозь электроды электронов от напряжения между электродами. Сравните свои расчеты с экспериментальным графиком на рисунке 107.
Задача 2. Электроны с пренебрежимо малой начальной скоростью пролетают ускоряющие электроды. Постройте зависимость квадрата скорости пролетевших сквозь электроды электронов от напряжения между электродами. Сравните свои расчеты с экспериментальным графиком на рисунке 107.
Указание: при сравнении графиков зависимостей удобно использовать безразмерные переменные — v2/c2 и eU/mc2, указанные на рисунке.
Как следует из решения задачи, ожидаемая зависимость квадрата скорости частицы от ускоряющего потенциала — прямая пропорциональная. Эксперимент же дает нелинейную зависимость. Кроме того, при любых значениях ускоряющей разности потенциалов скорость не превышает скорости света. Не только этот эксперимент, но и другие эксперименты самого разного характера показывают, что в любой системе отсчета скорость материальных тел не может превышать скорости света.
Вопрос 1. Что можно сказать о зависимости кинетической энергии электрона от скорости (учтите результаты описанного выше эксперимента)?
Из вышеописанного опыта можно сделать выводы: скорость электронов не может превышать скорости света; при движении электронов с большими скоростями их запасенная энергия не равна ![]() .
.
1.3 Возможные способы решения парадоксов
Мы рассмотрели только малую часть экспериментальных фактов, которые не согласуются с усвоенными ранее представлениями из электродинамики и из механики. На самом деле список физических явлений, для понимания которых приходится пересматривать казавшиеся надежными знания классической физики, очень широк. Столкнувшись с данным обстоятельством, физики были вынуждены пересмотреть законы классической физики.
Для разрешения противоречия при попытке рассмотрения из разных систем отсчета явлений типа взаимодействия движущихся заряженных частиц Г. Лоренц предположил, что все движущиеся тела сжимаются в направлении движения. Тогда оказывается возможным согласование выводов о поведении взаимодействующих электронов с точки зрения наблюдателей из разных систем отсчета. Так, с точки зрения наблюдателя, движущегося вместе с электроном вдоль провода с током, провод оказывается более коротким, чем покоящийся провод. При этом плотность положительных зарядов ионов решетки оказывается большей, чем плотность зарядов электронов проводимости. Положительные и отрицательные заряды не вполне скомпенсированы. Провод в целом оказывается положительно заряженным и притягивает отрицательно заряженный электрон. Так что из обеих систем отсчета должно наблюдаться притяжение электрона к проводу. Противоречие снимается. Предположение Лоренца указывает на то, что электрические и магнитные поля относительны. Если в некоторой системе отсчета имеется только магнитное поле, а электрического поля нет, то обязательно найдется система отсчета, в которой есть и электрическое поле. Г. Лоренц показал, что преобразования Галилея координат частиц и их скоростей при переходе из одной инерциальной системы отсчета в другую надо видоизменить, и тогда никаких электродинамических парадоксов не возникает. Найденные им преобразования назвали преобразованиями Лоренца.


