Электромагнитные волны
Электромагнитные волны
Представим, что в некоторой точке внутри безграничной непроводящей среды создано каким-либо способом электрическое поле ![]() . Если нет зарядов, поддерживающих это поле, то оно будет исчезать. Но убывающее поле
. Если нет зарядов, поддерживающих это поле, то оно будет исчезать. Но убывающее поле ![]() , согласно уравнений Максвелла, вызывает возникновение магнитного поля:
, согласно уравнений Максвелла, вызывает возникновение магнитного поля:
 0
0
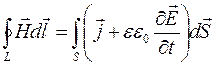 .
.
Поскольку поле ![]() убывает, то плотность тока смещения
убывает, то плотность тока смещения 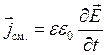 направлена противоположно
направлена противоположно ![]() и силовые линии магнитного поля направлены по часовой стрелке.
и силовые линии магнитного поля направлены по часовой стрелке.
Поскольку нет постоянных токов, поддерживающих ![]() , то последнее будет в свою очередь исчезать, и вызовет вихревое электрическое поле:
, то последнее будет в свою очередь исчезать, и вызовет вихревое электрическое поле:
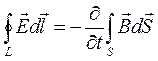
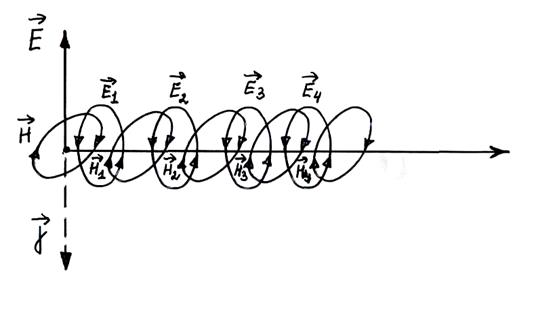 Силовые линии будут направлены против часовой стрелки. Поле
Силовые линии будут направлены против часовой стрелки. Поле ![]() уничтожит первоначальное поле
уничтожит первоначальное поле ![]() в начальной точке, но зато проявится в соседней точке 1. Исчезая в точке 1, электрическое поле
в начальной точке, но зато проявится в соседней точке 1. Исчезая в точке 1, электрическое поле ![]() приведет к появлению магнитного поля
приведет к появлению магнитного поля ![]() , которое будет иметь такое же направление, как и поле
, которое будет иметь такое же направление, как и поле ![]() . Поле
. Поле ![]() уничтожит поле
уничтожит поле ![]() и обнаружится в более удаленной точке. Таким образом, вместо первоначального поля
и обнаружится в более удаленной точке. Таким образом, вместо первоначального поля ![]() получим электрическое и магнитное поля, взаимно связанные друг с другом и распространяющиеся в пространстве, то есть электромагнитную волну.
получим электрическое и магнитное поля, взаимно связанные друг с другом и распространяющиеся в пространстве, то есть электромагнитную волну.
Для вакуума основные уравнения Максвелла принимают вид:
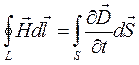 ;
; 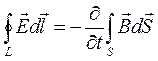 ;
;
причем 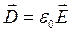 ,
, 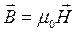
Описываемые этими уравнениями поля не связаны ни с зарядами, ни с токами проводимости и являются самостоятельно существующей реальностью. Это одна из форм существования материи – электромагнитное поле. В дифференциальной форме:
 ;
; 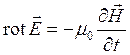 ;
;
Видно, что векторы напряженностей и индукций поля имеют вихревой характер, то есть линии всех полей замкнуты на себя. Общее решение уравнений затруднительно. Поэтому рассмотрим одномерный случай: оба поля будут изменяться только вдоль одной оси (например ![]() ) и времени (плоское поле). Фронтом волны называют поверхность, во всех точках которой колебания имеют одинаковую фазу. Рассматриваемая одномерная задача соответствует плоским электромагнитным волнам. Производные
) и времени (плоское поле). Фронтом волны называют поверхность, во всех точках которой колебания имеют одинаковую фазу. Рассматриваемая одномерная задача соответствует плоским электромагнитным волнам. Производные 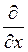 и
и ![]() обращаются в ноль. Уравнения Максвелла примут вид:
обращаются в ноль. Уравнения Максвелла примут вид:
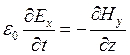 ;
; 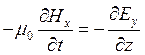
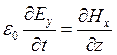 ;
; 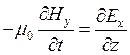
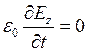 ;
; 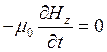
Из 2-х последних уравнений: ![]() ,
, 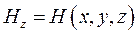 . Эти уравнения описывают не зависящие от времени постоянные поля. Они нас не интересуют. Можно положить
. Эти уравнения описывают не зависящие от времени постоянные поля. Они нас не интересуют. Можно положить 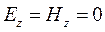 .Рассмотрим два уравнения:
.Рассмотрим два уравнения:
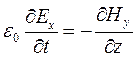 ;
; 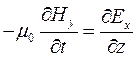 ;
;
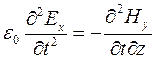 ;
; 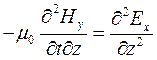
Следовательно:
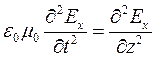
Исключая ![]() можно получить:
можно получить:
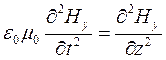
Величина 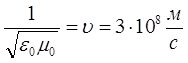 – скорость распространения электромагнитной волны в вакууме. Тогда:
– скорость распространения электромагнитной волны в вакууме. Тогда:
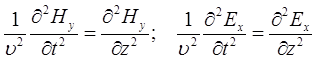
Полученные уравнения называют волновыми уравнениями. Простейшим решением рассматриваемых волновых уравнений являются функции:
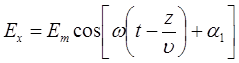 ,
, 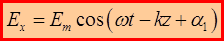 ,
,
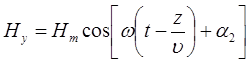 ,
,  ,
,
где ![]() – частота волны,
– частота волны, 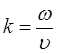 – волновое число,
– волновое число, ![]() и
и ![]() – начальные фазы. После подстановки в уравнения:
– начальные фазы. После подстановки в уравнения:
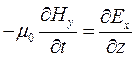
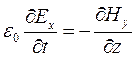
получаем:
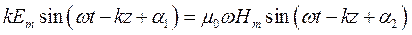
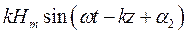 =
=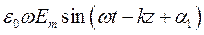
Необходимо: 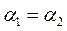
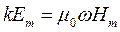 ;
; 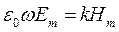 ;
;
Перемножив:
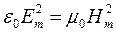 ;
;
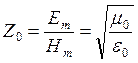 = 377 Ом – волновое сопротивление вакуума.
= 377 Ом – волновое сопротивление вакуума.
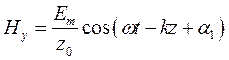
Умножив: 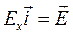 ,
, 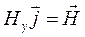 получим уравнение плоской электромагнитной волны в векторном виде:
получим уравнение плоской электромагнитной волны в векторном виде:
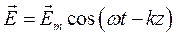 ,
, 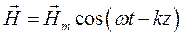 ,
, 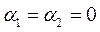
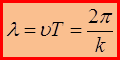 – длина волны.
– длина волны.
Векторы ![]() и
и ![]() образуют с направлением распространения волны правовинтовую систему.
образуют с направлением распространения волны правовинтовую систему.
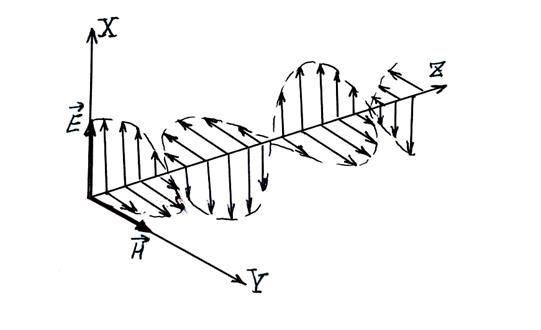 Плоскость, проходящая через электрический вектор
Плоскость, проходящая через электрический вектор ![]() и, в данном случае, ось OZ называется плоскостью поляризации линейно поляризованной волны.
и, в данном случае, ось OZ называется плоскостью поляризации линейно поляризованной волны.
Энергия электромагнитных волн
Электромагнитные волны переносят определенную энергию. Объемная плотность энергии электромагнитного поля в вакууме:
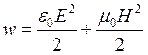
Поскольку 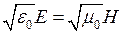 , то
, то
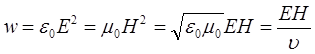 ,
,
где ![]() – скорость электромагнитных волн в вакууме.
– скорость электромагнитных волн в вакууме.
Вектор плотности потока энергии электромагнитной волны называется вектором Умова-Пойнтинга ![]() (иногда вектором Пойнтинга):
(иногда вектором Пойнтинга):
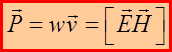
Вычислим энергию ![]() , переносимую электромагнитной волной через площадку
, переносимую электромагнитной волной через площадку ![]() за время
за время ![]() :
:
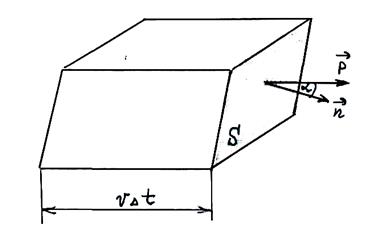
![]() – объем параллелепипеда
– объем параллелепипеда
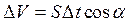
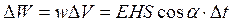
Следовательно, энергия, проходящая через площадку S в единицу времени:
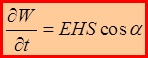
или
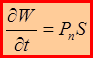
В случае плоской линейно поляризованной монохроматической волны, распространяющейся вдоль положительного направления оси OZ, напряженность поля
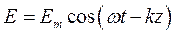 .
.
Соответственно:
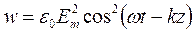 .
.
Значение ![]() в каждой точке периодически колеблется. Среднее за период значение
в каждой точке периодически колеблется. Среднее за период значение ![]() пропорционально квадрату амплитуды:
пропорционально квадрату амплитуды:
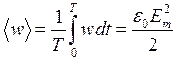 .
.
Излучение электромагнитных волн
Для образования электромагнитных волн необходимо создать в пространстве быстро изменяющееся электрическое поле (ток смещения) и соответственно быстро изменяющееся магнитное поле. Для этого используется открытый колебательный контур.
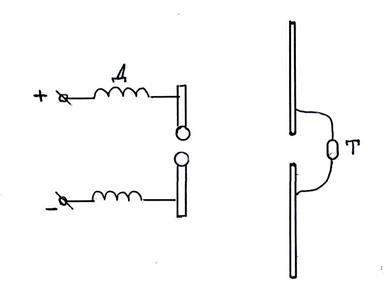 Свободные электромагнитные волны были впервые получены на опыте Генрихом Герцем в 1888 году. Использовался открытый вибратор, состоящий из двух одинаковых металлических стержней, разделенных искровым промежутком. При пробойном значении напряжения в пробойнике проскакивает искра, замыкавшая обе половины вибратора, и в нем возникали затухающие электрические колебания высокой частоты. Для обнаружения электромагнитных волн Герц применял вибраторы различной формы: Т – миниатюрная газоразрядная трубка. Размеры излучающего и принимающего вибраторов одинаковы, чтобы возник резонанс. По свечению газоразрядной трубки Т обнаруживались электромагнитные волны.
Свободные электромагнитные волны были впервые получены на опыте Генрихом Герцем в 1888 году. Использовался открытый вибратор, состоящий из двух одинаковых металлических стержней, разделенных искровым промежутком. При пробойном значении напряжения в пробойнике проскакивает искра, замыкавшая обе половины вибратора, и в нем возникали затухающие электрические колебания высокой частоты. Для обнаружения электромагнитных волн Герц применял вибраторы различной формы: Т – миниатюрная газоразрядная трубка. Размеры излучающего и принимающего вибраторов одинаковы, чтобы возник резонанс. По свечению газоразрядной трубки Т обнаруживались электромагнитные волны.
ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ.
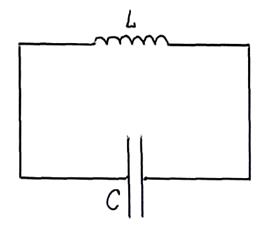 Электрический колебательный контур
Электрический колебательный контур
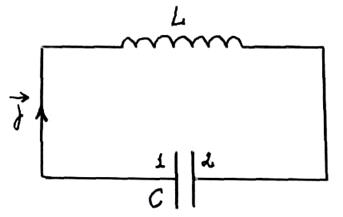
В цепи, содержащей индуктивность L (катушку) и емкость C (конденсатор), могут возникать электромагнитные колебания, при которых электрические величины (заряды, токи, электрические и магнитные поля) изменяются периодически. Поэтому такая цепь называется колебательным контуром.
Колебания в контуре можно вызвать либо сообщив обкладкам конденсатора некоторый начальный заряд, либо возбудив в индуктивности ток (например, путем выключения внешнего магнитного поля, пронизывавшего витки катушки). Рассмотрим первый способ.
1 2 3 4 5
![]()
![]()
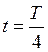
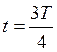
![]()
|
|
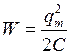
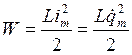
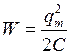
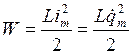
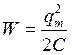
|
|
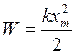
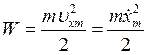
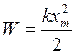
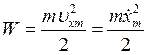
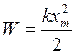
Пусть отключенный от индуктивности конденсатор присоединен к источнику напряжения. Это приводит к возникновению на обмотках разноименных зарядов +q и – q. Между обкладками возникает электрическое поле, максимальная энергия которого равна ![]() . После отключения от источника напряжения конденсатор емкость начнет разряжаться и в контуре потечет Электрический ток. Энергия электрического поля будет уменьшаться, но зато будет увеличиваться энергия возникающего магнитного поля, обусловленного током, текущим через индуктивность. Максимальное значение этой энергии
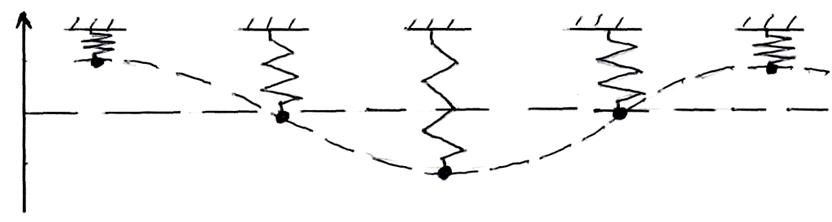
. После отключения от источника напряжения конденсатор емкость начнет разряжаться и в контуре потечет Электрический ток. Энергия электрического поля будет уменьшаться, но зато будет увеличиваться энергия возникающего магнитного поля, обусловленного током, текущим через индуктивность. Максимальное значение этой энергии ![]() . Поскольку активное сопротивление контура равно нулю, то полная энергия, слагающаяся из энергий электрического и магнитного полей, не расходуется на нагревание проводов и будет оставаться постоянной. Поэтому в момент, когда напряжение на конденсаторе, а, следовательно, и энергия электрического поля обращаются в нуль, энергия магнитного поля, а значит и ток достигают наибольшего значения. В дальнейшие моменты времени магнитное поле будет исчезать, поскольку нет токов, его поддерживающих. Исчезающее поле вызовет ток самоиндукции, который в соответствии с законом Ленца будет стремиться поддержать ток разряда конденсатора и будет, следовательно, направлен так же, как и последний. Поэтому конденсатор будет перезаряжаться и между его пластинами появится электрическое поле противоположного, по сравнению с начальным, направления. Затем те же процессы протекают в обратном направлении, после чего система переходит в исходное состояние. После чего весь цикл повторяется снова. В ходе процесса периодически изменяются (колеблются) заряд на обкладках, напряжение на конденсаторе и сила тока, текущего через индуктивность. Колебания сопровождаются взаимными превращениями энергий электрического и магнитного полей. Воспроизведем сказанное на рисунке, сопоставив рассматриваемому процессу процесс колебания пружинного маятника.
. Поскольку активное сопротивление контура равно нулю, то полная энергия, слагающаяся из энергий электрического и магнитного полей, не расходуется на нагревание проводов и будет оставаться постоянной. Поэтому в момент, когда напряжение на конденсаторе, а, следовательно, и энергия электрического поля обращаются в нуль, энергия магнитного поля, а значит и ток достигают наибольшего значения. В дальнейшие моменты времени магнитное поле будет исчезать, поскольку нет токов, его поддерживающих. Исчезающее поле вызовет ток самоиндукции, который в соответствии с законом Ленца будет стремиться поддержать ток разряда конденсатора и будет, следовательно, направлен так же, как и последний. Поэтому конденсатор будет перезаряжаться и между его пластинами появится электрическое поле противоположного, по сравнению с начальным, направления. Затем те же процессы протекают в обратном направлении, после чего система переходит в исходное состояние. После чего весь цикл повторяется снова. В ходе процесса периодически изменяются (колеблются) заряд на обкладках, напряжение на конденсаторе и сила тока, текущего через индуктивность. Колебания сопровождаются взаимными превращениями энергий электрического и магнитного полей. Воспроизведем сказанное на рисунке, сопоставив рассматриваемому процессу процесс колебания пружинного маятника.
Из сопоставления электромагнитных колебаний следует, что энергия электрического поля ![]() аналогична потенциальной энергии упругой деформации, а энергия магнитного поля
аналогична потенциальной энергии упругой деформации, а энергия магнитного поля ![]() аналогична кинетической энергии. Индуктивность
аналогична кинетической энергии. Индуктивность ![]() аналогична массе
аналогична массе ![]() ; величина, обратная емкости аналогична жесткости пружины
; величина, обратная емкости аналогична жесткости пружины ![]() . Заряду
. Заряду ![]() соответствует изменение координаты центра колеблющегося груза от положения равновесия
соответствует изменение координаты центра колеблющегося груза от положения равновесия ![]() , а силе тока
, а силе тока ![]() – проекция скорости центра груза
– проекция скорости центра груза ![]() .
.
Собственные колебания
Гармонические колебания
 Электрические колебания, происходящие под действием процессов, развивающихся в самом колебательном контуре, получили название собственных электрических колебаний. Рассмотренные выше колебания являются, очевидно, собственными. Рассмотрим количественно собственные колебания в контуре. Будем считать, что электрические процессы в контуре квазистационарны. То есть мгновенное значение силы тока i одно и тоже в любом месте контура. Поэтому мгновенные значения
Электрические колебания, происходящие под действием процессов, развивающихся в самом колебательном контуре, получили название собственных электрических колебаний. Рассмотренные выше колебания являются, очевидно, собственными. Рассмотрим количественно собственные колебания в контуре. Будем считать, что электрические процессы в контуре квазистационарны. То есть мгновенное значение силы тока i одно и тоже в любом месте контура. Поэтому мгновенные значения ![]() силы переменного тока должны удовлетворять всем законам, установленным для постоянного тока.
силы переменного тока должны удовлетворять всем законам, установленным для постоянного тока.
Согласно закону Ома для участка цепи 1LR2 имеем:
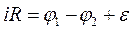 ;
;
где 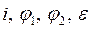 – мгновенные значения силы тока в цепи, потенциалы на обкладках конденсатора и алгебраические суммы ЭДС, приложенных на рассматриваемом участке цепи. Но на участке цепи приложена только ЭДС самоиндукции
– мгновенные значения силы тока в цепи, потенциалы на обкладках конденсатора и алгебраические суммы ЭДС, приложенных на рассматриваемом участке цепи. Но на участке цепи приложена только ЭДС самоиндукции
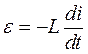 .
.
Поэтому записанное уравнение примет вид:
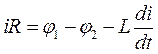 .
.
Если обозначить заряд первой обкладки конденсатора ![]() , то сила тока
, то сила тока ![]() в цепи равна:
в цепи равна:
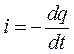 и
и 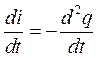
Знак минус введен, потому что положительному направлению тока i, принятому при составлении уравнения, выражающему закон Ома, соответствует убывание положительного заряда первой обкладки конденсатора 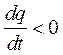 .
.
Напряжение: 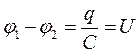 .
.
После подстановки получим:
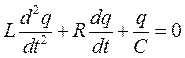 , или
, или 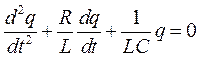 .
.
Если сопротивление R = 0 (что соответствует рассматриваемому контуру), то:
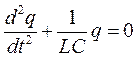 ; или
; или 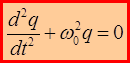 , где
, где 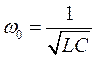 .
.
Полученное дифференциальное уравнение описывает колебательное движение. Решением этого уравнения является функция:
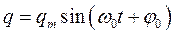
Следовательно: заряд на обкладках конденсатора изменяется по гармоническому закону. Частота ![]() называется собственной частотой контура. Для периода колебаний (период связан с частотой соотношением
называется собственной частотой контура. Для периода колебаний (период связан с частотой соотношением 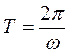 ) получаем: так называемая.
) получаем: так называемая.
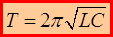 – формула Томсона.
– формула Томсона.
Разность потенциалов обкладок конденсатора 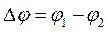 также изменяется по гармоническому закону:
также изменяется по гармоническому закону:
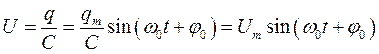 , где
, где 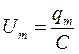
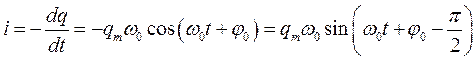
Видно, что сила тока отстает от колебаний напряжения на обкладках конденсатора по фазе на ![]() . Сопоставление формул для q, U, i показывает, что когда модуль силы тока достигает наибольшего значения, модули заряда и напряжения обращаются в нуль и наоборот. Это соотношение между зарядом и током установлены ранее, основываясь на энергетических соображений. Из формул:
. Сопоставление формул для q, U, i показывает, что когда модуль силы тока достигает наибольшего значения, модули заряда и напряжения обращаются в нуль и наоборот. Это соотношение между зарядом и током установлены ранее, основываясь на энергетических соображений. Из формул:
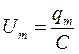 ,
, 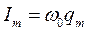
Следует: 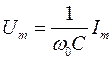 ;
; 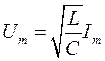
![]() – волновое сопротивление колебательного контура.
– волновое сопротивление колебательного контура.