Емкость уединенного проводника и системы проводников

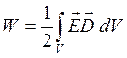, (4.5)

где – вектор электрической индукции. Для изотропного однородного диэлектрика напряженность и индукция электрического поля связаны как

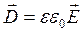, (4.6)

где – диэлектрическая проницаемость среды, в которой создано электрическое поле.

Отметим, что в случае расчета энергии заряженного тела интегрирование ведем по кривой, поверхности или объему тела, а при расчете энергии поля – по всему пространству (до бесконечности).

Темы для развернутых ответов

1.  Энергия заряженного тела. Примеры.

2.  Энергия электрического поля.

Литература: [1], глава 2, §18; [3], глава 1, §15,16; глава 2, §22,23.

Основной блок задач

1.  Шар радиуса равномерно заряжен по объему с плотностью заряда . Рассчитайте потенциальную энергию этого шара.

2.  Проверьте правильность выполнения задачи 1 с помощью формулы энергии электрического поля 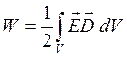. По какой области необходимо производить интегрирование?

3.  Дан металлический шар радиуса с зарядом . Вычислите потенциал электрического поля и энергию этого шара.

Дополнительный блок задач

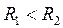4.  Пространство между двумя концентрическими сферами с радиусами и () заряжено с объемной плотностью 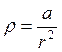. Найдите полный заряд и потенциал электрического поля для данного тела. Рассчитайте энергию этого заряженного тела двумя способами (как энергию тела и поля).

Практическое занятие №5

Емкость уединенного проводника и системы проводников

Краткие теоретические сведения

Емкостью уединенного проводника называется отношение его заряда к потенциалу

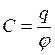. (5.1)

Конденсатором называется совокупность двух любых проводников с одинаковыми по мродулю, но противоположными по знаку зарядами. Емкость конденсатора определяется соотношением

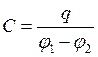, (5.2)

где – абсолютное значения заряда одного из проводников, 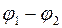– разность потенциалов. Емкость конденсатора зависит только от геометрических характеристик проводников и их взаимного расположения.

В общем случае при рассмотрении системы из большого числа заряженных проводников в рассмотрение вводят емкостные коэффициенты – емкость -го проводника относительно -го. Расчет емкостных коэффициентов в такой ситуации – сложная математическая задача.

Энергия конденсатора как системы из двух проводников определяется по формуле

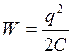, (5.3)

откуда можем выразить емкость как

. (5.4)

Расчет емкости конденсатора упрощается тем, что его электрическое поле сосредоточено между обкладками.

Расчет емкости конденсатора по определению:

1.  Выбираем произвольную точку внутри конденсатора и находим значение вектора электрической индукции в выбранной точке

2.  По материальному уравнению вычисляем напряженность в данной точке.

3.  По определению разности потенциалов рассчитываем (для уединенного тела – просто его потенциал).

4.  Зная и (произвольное значение), по формуле рассчитываем емкость.

Расчет емкости конденсатора по формуле энергии:

1.  Выбираем произвольную точку внутри конденсатора и находим значение вектора электрической индукции в выбранной точке (по теореме Остроградского-Гаусса).

2.  По материальному уравнению вычисляем напряженность в данной точке.

3.  По выражениям для и рассчитываем энергию электрического поля конденсатора. Интегрируем по бесконечному объему (если поле не замкнуто внутри конденсатора) или по объему конденсатора.

4.  По формуле рассчитываем емкость системы.

Темы для развернутых ответов

1.  Электрическая емкость системы проводников.

2.  Расчет электрической емкости конденсатора на конкретном примере (2 способа).

Литература: [1], глава 2, §16; [3], глава 1, §5,9; глава 2, §22,23.

Основной блок задач

1.  Вычислить емкость уединенной металлической сферы известного радиуса.

2.  Дан плоский конденсатор с площадью пластин и расстоянием между ними . Пространство между пластинами заполнено диэлектриком с проницаемостью . Рассчитайте емкость конденсатора двумя способами.