Энтропия изолированной термодинамической системы
Изменение энтропии этой изолированной ТС будет равна сумме изменений энтропий тел №1 и №2 т. к. энтропия — величина аддитивная:
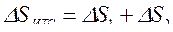 ,
,
или 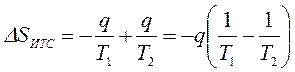 ,
,
где знак минус перед q/T1 означает, что тело №1 отводит теплоту, а знак плюс перед q/T2 означает, что к телу №2 подводится теплота.
Так как Т1>Т2, то 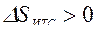 , т. е. в результате неравновесного теплообмена энтропия ИТС возрастает.
, т. е. в результате неравновесного теплообмена энтропия ИТС возрастает.
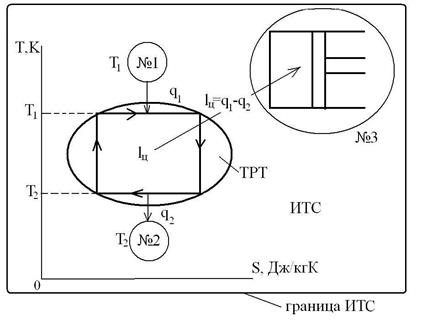
Для равновесного перехода теплоты от тела №1 к телу №2 необходим посредник – термодинамическое рабочее тело (ТРТ), которое могло бы совершать обратимый цикл Карно, взаимодействуя с телами №1 и №2, как с источником теплоты и холодильником. Тело №3 – аккумулятор работы, который равновесно воспринимает от рабочего тела механическую работу. Тогда 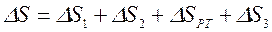 , где
, где 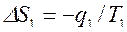 ,
, 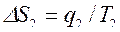 ,
, 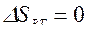 , т. к. совершив цикл, ТС возвращается в исходное состояние, и
, т. к. совершив цикл, ТС возвращается в исходное состояние, и 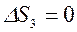 , т. к. тело №3 не участвует в теплообмене.
, т. к. тело №3 не участвует в теплообмене.
Тогда 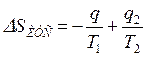 (с учетом знаков, принятых в термодинамике). Для цикла Карно известно, что термический коэффициент полезного действия цикла равен
(с учетом знаков, принятых в термодинамике). Для цикла Карно известно, что термический коэффициент полезного действия цикла равен 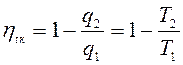 , или
, или 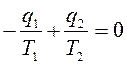 , т. е. сумма приведенных теплот цикла Карно равна нулю. Следовательно, изменение энтропии ИТС
, т. е. сумма приведенных теплот цикла Карно равна нулю. Следовательно, изменение энтропии ИТС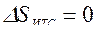 .
.
6.3. Энтропия изолированной термодинамической системы
Изолированная ТС – система без обмена энергией и веществом с окружающей средой (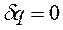 ,
, 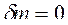 ). Для обратимых равновесных процессов в ИТС энтропия остается неизменной:
). Для обратимых равновесных процессов в ИТС энтропия остается неизменной: 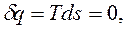
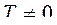 . Тогда ds=0,
. Тогда ds=0, ![]() ,
, ![]() .
.
Для необратимых, неравновесных процессов в ИТС энтропия всегда возрастает:
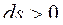 ,
, 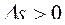 ,
, 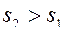 .
.
Переход ИТС из одного состояния в другое с помощью неравновесных процессов сопровождается выравниванием параметром в системе и образованием теплоты наинизшей температуры. Количество энергии ИТС остается неизменным, но энергия теряет способность совершать работу, т. е. происходит обесценивание энергии.
Таким образом, энтропия является мерой рассеяния энергии, мерой ее обесценивания. На этом основании Клаузиус выдвинул концепцию «тепловой смерти» Вселенной. Больцман в противовес этой концепции Клаузиуса установил статистическую природу 2-го закона термодинамики, получив связь между энтропией ТС S и термодинамической вероятностью состояния ТС W:
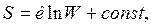
где 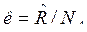 — постоянная Больцмана;
— постоянная Больцмана; ![]() =8,31441Дж/мольК – молярная газовая постоянная; NA=6,02
=8,31441Дж/мольК – молярная газовая постоянная; NA=6,02![]() моль-1 – число Авогадро; W – термодинамическая вероятность состояния ТС, определяемая числом микросостояний, реализующих данное макросостояние.
моль-1 – число Авогадро; W – термодинамическая вероятность состояния ТС, определяемая числом микросостояний, реализующих данное макросостояние.
В соответствии с концепцией Больцмана тепловое беспорядочное движение частиц является более вероятным движением, чем организованное, направленное движение частиц – работа. Поэтому организованное движение частиц (работа) и стремится перейти к беспорядочному движению (теплоте). Этим объясняется односторонний характер изменения энтропии в ИТС при переходе из менее вероятного в более вероятное состояние. Проблему же «тепловой смерти» Вселенной в настоящее время нельзя даже ставить, поскольку общая теория относительности (ОТО) и новая релятивистская теория гравитации (РТГ) позволяет сделать вывод, что эволюция Вселенной, которую она испытывает во времени, не представляет собой приближения ее состояния к некоторому равновесному состоянию – состоянию «тепловой смерти».
ГЛАВА 7. ОБЪЕДИНЕННЫЕ ВЫРАЖЕНИЯ ПЕРВОГО И ВТОРОГО ЗАКОНОВ ТЕРМОДИНАМИКИ
7.1. Различные формы записи объединенных выражений
Для сложных открытых ТС уравнения первого закона термодинамики, выраженные через изменения внутренней энергии и энтальпии имеют вид:
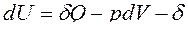 ℒ
ℒ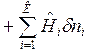 ,
,
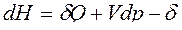 ℒ
ℒ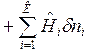 .
.
Математическое выражение 2-го закона термодинамики:
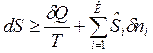 ,
,
представим в виде: 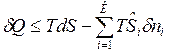 , и подставим в уравнение 1-го закона термодинамики.
, и подставим в уравнение 1-го закона термодинамики.
Тогда получим объединенные выражения для изменения внутренней энергии dU и энтальпии dH:
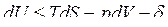 ℒ
ℒ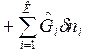 , (1)
, (1)
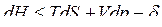 ℒ (2)
ℒ (2)
где 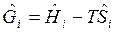 — молярная свободная энергия Гиббса, Дж/моль.
— молярная свободная энергия Гиббса, Дж/моль.
G=H-TS, Дж, — свободная энергия Гиббса, которая является функцией состояния. Функцией состояния является также свободная энергия Гельмгольца:
F=U-TS Дж.
Дифференциалы dF и dG – полные дифференциалы:
dF=dU-TdS-SdT,
dG=dH-TdS-SdT.
Вместо dU и dH подставим в эти выражения их значения по уравнениям (1) и (2). Тогда получим еще две формы записи объединенных выражений 1-го и 2-го законов термодинамики для функций F и G:
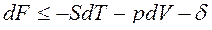 ℒ
ℒ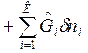 , (3)
, (3)


