электромагнитные волны

Если нет источников, система уравнений Максвелла определяет свободное электромагнитное излучение. В случае вакуума простейшее решение этих уравнений описывает свободную электромагнитную волну, имеющую постоянные амплитуду и частоту, определенную поляризацию и плоский фазовый фронт. Электромагнитное поле плоской монохроматической волны, бегущей в положительном направлении оси и линейно поляризованной по оси , имеет вид:

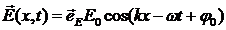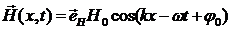, . (3.1)

Здесь 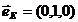— безразмерный единичный вектор поляризации, задающий ориентацию вектора , — амплитуда электрического поля (амплитуда волны) имеющая размерность В/м, 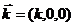— волновой вектор, — волновое число, — длина волны, — круговая частота, — фазовая скорость плоской волны в вакууме, равная скорости света , 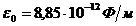— электрическая постоянная, 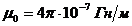— магнитная постоянная, — период волны, аргумент косинуса 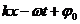— фаза волны, — постоянная начальная фаза волны, 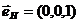— единичный вектор, задающий ориентацию вектора , — амплитуда магнитного поля, имеющая размерность А/м.

Фазовый фронт (волновая поверхность) волны (3.1) есть плоскость, перпендикулярная оси и перемещающаяся в положительном направлении этой оси с фазовой скоростью . Электромагнитная волна (3.1) является поперечной, поскольку векторы и совершают гармонические колебания в плоскости, перпендикулярной к направлению распространения волны. Векторы , и образуют правую тройку (см. рис. 3.1). Для плоской монохроматической волны в вакууме амплитуды электрического и магнитного полей связаны между собой соотношением

, (3.2)

которое означает равенство плотностей энергии электрического и магнитного полей.

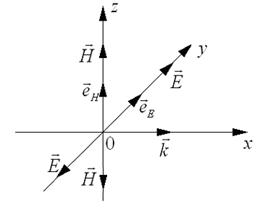
Рис. 3.1

Действующим на вещество полем в электромагнитной волне обычно считается электрическое поле, поскольку взаимодействием магнитного поля и заряженных частиц вещества, имеющих скорость 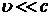, в большинстве случаев можно пренебречь.

Плотность энергии электромагнитной волны равна сумме плотностей энергии электрического и магнитного полей

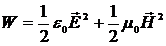. (3.3)

Усредняя величину по времени 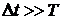, легко получить

. (3.4)

Здесь использовано соотношение (3.2), благодаря которому плотность энергии электрического поля равна плотности магнитного поля.

Пространственный перенос энергии электромагнитного поля электромагнитной волной описывается с помощью вектора Пойнтинга – вектора плотности потока энергии

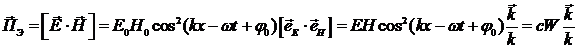. (3.5)

Величина вектора Пойнтинга численно равна энергии, переносимой волной за единицу времени через единичную площадку, которая ориентирована перпендикулярно к волновому вектору. Интенсивность волны определяется формулой

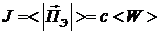. (3.6)

Вектор Пойнтинга и интенсивность имеют одинаковую размерность .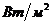

Вместе с энергией волна (3.1) переносит импульс электромагнитного поля. Плотность потока импульса

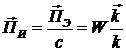. (3.7)

Если взаимодействие со средой меняет импульс волны, то в соответствии с III-им законом Ньютона возникает сила, действующая со стороны волны на эту среду. Волна, нормально падающая на поверхность среды, которая полностью поглощает эту волну, создает давление на среду, равное плотности энергии . Если нормально падающая волна полностью отражается, то соответствующее давление удваивается и равно .

Отметим, что полная сила с которой солнечное излучение действует на Землю, примерно равна 109 Н. Сфокусированное излучение наиболее мощных современных лазеров способно создавать импульсы давления, имеющие длительность ~10–17с и амплитуду ~1016Па, которая сравнима с давлением в центре Солнца.