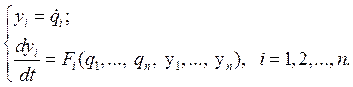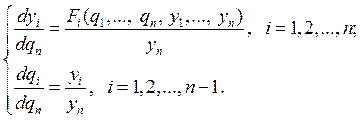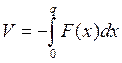Фазовое пространство, представление движения
(1.30)
Из (1.30) можно непосредственно найти первый интеграл движения:
|
|
(1.31) |
Коэффициенты Ci можно найти из начальных условий.
Лагранжев формализм работает только в потенциальном поле, но, если в системе действуют диссипативные силы Qi (трение, потери), то в общем случае уравнение Лагранжа выглядит так:
|
|
(1.32) |
Простейший случай, когда диссипативные силы являются линейной функцией обобщённых скоростей:
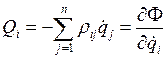 .
.
Для линейной функции можно построить функцию Рэлея, тогда диссипативные силы — это частные производные по обобщённым координатам функции Рэлея:
|
|
(1.33) |
В этом случае уравнение Лагранжа примет ещё более простой вид:
|
|
(1.34) |
т. е. для полного описания системы с диссипацией нужно задать две функции: L и F.
Если точечное преобразование (1.28) не содержит в явном виде времени, то
|
|
(1.35) |
Таким образом, энергия системы убывает со скоростью, равной удвоенной функции Рэлея.
1.6. Фазовое пространство, представление движения
Движение любой системы описано полностью, если задан закон изменения во времени всех обобщённых координат ![]() . Но, задание точи
. Но, задание точи ![]() в момент времени t определяет лишь текущее положение системы, но ничего не говорит о её динамике. Через одну точку в координатном пространстве может проходить множество траекторий, которые в данной точке отличаются значениями обобщённых скоростей. Поэтому более наглядно анализировать движение в 2n-мерном фазовом пространстве
в момент времени t определяет лишь текущее положение системы, но ничего не говорит о её динамике. Через одну точку в координатном пространстве может проходить множество траекторий, которые в данной точке отличаются значениями обобщённых скоростей. Поэтому более наглядно анализировать движение в 2n-мерном фазовом пространстве 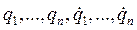 .
.
Выбор любой точки в фазовом пространстве (за исключением нескольких особых точек) в силу теоремы о существовании и единственности решения ДУ вида (1.26) полностью определяет дальнейшее движение системы. Кроме, может быть, особых точек, траектории в фазовом пространстве не пересекаются.
Рассмотрим автономную систему с n степенями свободы. Её ДУ, записанное в форме Коши (1.26), сведётся к виду:
|
|
(1.36) |
Введём новые переменные 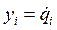 , тогда получим каноническое уравнение движения:
, тогда получим каноническое уравнение движения:
|
|
(1.37) |
Чтобы получить фазовую траекторию, необходимо убрать время в явном виде, тогда исключим из (1.37) dt. Для этого разделим первые 2n — 1 уравнений системы на её последнее уравнение:
|
|
(1.38) |
Во всех точках фазового пространства, где однозначно определены правые части системы уравнений (1.38), угловые коэффициенты касательных dyi/dqn и dqi/dqn единственным образом определяют фазовую траекторию. Через каждую такую точку проходит одна траектория, время t играет роль параметра. Через особую точку, где не определены правые части системы уравнений (1.38), может проходить бесконечное множество траекторий, или не проходить ни одной (например, точка равновесия).
Если система неавтономна, то правые части системы уравнений (1.36) зависят ещё и от времени t, следовательно, для анализа движения нужно 2n + 1 расширенное фазовое пространство, в котором есть ось времени.
Тема 2. Консервативные системы с одной степенью свободы Вопрос 4
Как известно, консервативные системы — это системы, в которых сохраняется полная колебательная энергия. Одна степень свободы говорит о том, что колебательный процесс описывается одной обобщённой координатой. Понятно, что это некоторая идеализация (абсолютно консервативных систем не существует), однако, возможны системы, которые к ним достаточно близки (высокодобротный колебательный контур, маятник с малым затуханием на хорошем подвесе). В любом случае, тому, что энергия сохраняется, отвечают, например, колебательные системы, которые описываются уравнениями вида (1.36) при условии, что правая часть зависит от обобщённых координат, но не от обобщённых скоростей, т. е. 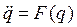 (здесь все множители нормированы на единицу массы). Тогда выражение для кинетической энергии должно иметь вид:
(здесь все множители нормированы на единицу массы). Тогда выражение для кинетической энергии должно иметь вид:
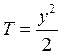 ,
,
где ![]() (обобщённая скорость). Так как потенциальная сила есть производная потенциальной величины по обобщённой координате, тогда сама потенциальная энергия есть интеграл
(обобщённая скорость). Так как потенциальная сила есть производная потенциальной величины по обобщённой координате, тогда сама потенциальная энергия есть интеграл
|
|
(2.1) |
(здесь в положении q0 просто ставится ноль потенциальной энергии).
Ниже следуют примеры консервативных систем.
1. Груз массы m на пружине жёсткостью k. Его колебания описываются уравнением 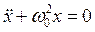 , где
, где 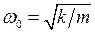 .
.
2. Резонансный LC-контур без сопротивления: 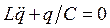 , где q — заряд на пластинах конденсатора.
, где q — заряд на пластинах конденсатора.
3. Математический маятник длиной l: 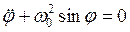 ,
, 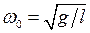 .
.
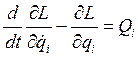 , где
, где 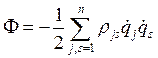
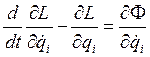 , где
, где 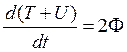 .
.