Гидравлическое моделирование

Для того чтобы оценить применение насадков и отверстий в различных технических устройствах, в таблице приведены некоторые их характеристики.

В том случае, когда мощность, уносимая потоком, должна иметь максимально возможное значение (сопла активных гидравлических турбин, гидромониторов, пожарных рукавов и т. п. устройств), применяют конические сходящиеся и коноидальные насадки. А, например, конические расходящиеся насадки имеют наименьшее значение мощности. Поэтому они получили широкое распространение как «отсасывающие трубы» реактивных гидравлических турбин и в других случаях, где требуется свести до минимума энергию в отходящем потоке.

8. Гидравлическое моделирование

8.1. Сущность моделирования

Моделированием называется исследование явлений на моделях. Сущность моделирования заключается в том, что на модели меньшего, а иногда и большего масштаба создается гидравлическое явление, подобно явлению, которое имеет место или должно возникнуть в натуре, что и позволяет изучить это явление. Основной задачей теории моделирования является выявление условий, обеспечивающих подобное явление. Явления называются подобными, если по известным характеристикам одного явления можно получить простым пересчетом аналогичные характеристики другого явления.

Одним из достоинств метода моделирования является возможность обобщения результатов единичного опыта на целый класс явлений. Этот метод, например, позволит результаты исследований движения воды обобщить на случай движения воздуха, масла и т. п., или наоборот. Даже больше, он позволяет распространить результаты исследования явления одного класса на явления другого, но описываемые одинаковыми математическими уравнениями. Метод моделирования обеспечивает наиболее рациональную организацию исследования, значительно сокращая тем самым объем экспериментальных работ, значит, и затраты средств, особенно, если исследования происходят на моделях, меньших натуры.

Научной базой моделирования является теория гидродинамического подобия, переплетающаяся теорией размерностей.

8.2. Основные законы гидродинамического подобия.

Критерий подобия Ньютона

Гидравлическое подобие складывается из трех составляющих: геометрического, кинематического и динамического.

Геометрическое подобие, как известно из геометрии, представляет собой пропорциональность сходственных размеров и равенство соответствующих углов. В гидравлике под геометрическим подобием понимают подобие тех поверхностей, которые ограничивают потоки, т. е. подобие шероховатости стенок, ограничивающих поток, в открытых потоках подобие свободных поверхностей, подобие запорных приспособлений, подобие твердых тел, помещаемых в натуре и в модели.

Если обозначить какие-либо характерные величины, например длину l, диаметр d, некоторую площадь или некоторый объем W, относящиеся к натуре, индексом «Н», а к модели — индексом «М», то между одноименными величинами геометрически подобных систем будет существовать соотношение

.

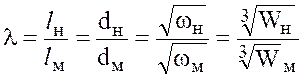Постоянная λ называется константой геометрического подобия.

Кинематическое подобие означает пропорциональность местных скоростей в сходственных точках и равенство углов, характеризующих направление этих скоростей.

Кинематическое подобие требует, чтобы траектории, описываемые соответствующими частицами потока натуры и модели, за любые соответствующие отрезки времени были подобны с константой подобия λ. Это значит, что зависимость между уравнениями траекторий соответствующих частиц должна определяться равенствами

,

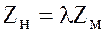в которых координаты являются функциями времени.

Примем, что если участки траектории и соответствующие частицы проходят за время tн и tм, то отношение 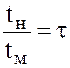должно быть независимым от времени и одним и тем же для любых соответствующих точек Uн и Uм, а именно:

.

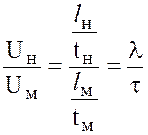Из условий кинематического и геометрического подобия вытекает зависимость между ускорениями ан и ам:

.

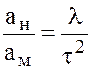Динамическое подобие – это пропорциональность сил, действующих на сходственные объемы в кинематически подобных потоках, и равенство углов, характеризующих направление этих сил.

В потоках жидкостей обычно действуют разные силы: давления, трения, тяжести и др. соблюдение их пропорциональности означает гидродинамические подобие. Силовое подобие требует, чтобы равнодействующие силы F = ma, действующие на соответствующие материальные частицы потока натуры и модели в соответствующие моменты времени, также находились бы в отношении

,

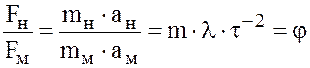где m, φ – соответственно масштабы массы и силы.

Из последнего выражения следует равенство

;

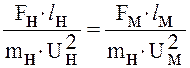величина

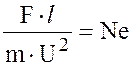(8.1)

называется критерием механического подобия – критерием Ньютона. Из полученного следует, что для любых двух соответствующих точек подобных потоков натуры и модели значения критерия механического подобия – числа Ньютона – имеют одно и то же значение, т. е. Neн. = Neм.

Критерий Ньютона является математическим выражением основного закона гидродинамического подобия.

8.3. Критерий подобия Рейнольдса, Фруда, Эйлера, Вебера

Критерий Ньютона Ne выражает зависимость между силами, массами, скоростями и линейными размерами в динамически подобных потоках в общем виде. В гидравлике приходится иметь дело главным образом с тремя видами сил: силой веса, силой давления и силой трения. В некоторых случаях приходится принимать во внимание силы поверхностного натяжения. При этом чаще всего в различных явлениях главную роль играет только один из этих видов сил. В общем, идеальном, случае полного подобия необходимо иметь подобие всех сил. Однако каждый их этих видов сил требует своих условий подобия, причем иногда несовместимых. Таким образом, удовлетворить основному условию подобия – равенству критериев Ньютона – не всегда возможно. В таких случаях необходимо обеспечить подобие того вида сил, который оказывается наиболее существенным в изучаемом явлении.

Критерии частичного подобия можно получить из критерия Ньютона, подставив в него, например, вместо силы F силу трения 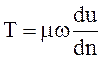, при этом получим условие подобия только сил трения (критерий Рейнольдса – Re), или силу тяжести G=mg – получим условие подобия только сил тяжести (критерий Фруда – Fr), или силу давления Р=р — условие подобия только сил давления (критерий Эйлера – Eu).

Подставим в выражение (8.1) силу трения Т:

.

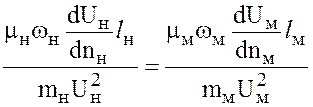Имея в виду, что 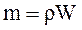, а в подобных системах