Интенсивность напряжения

с коэффициентами, равными инвариантам тензора напряжений. Использование теоремы Виета позволяет выразить инварианты через корни полученного характеристического уравнения

Т. к. собственные значения вещественного симметричного тензора второго ранга являются всегда вещественными числами, то главные напряжения всегда вещественны.

2.9 ИНТЕНСИВНОСТЬ НАПРЯЖЕНИЙЯ

В теории пластичности и механике разрушений часто используется величина, называемая интенсивностью напряжений. Прежде чем дать определение этой характеристики, введем некоторые новые объекты. Пусть выбрана декартова прямоугольная система координат. Построим по заданному тензору напряжений 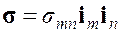его девиатор

Девиатор является также тензором второго ранга, поэтому рассмотрим инварианты этого тензора. Согласно общим формулам (2.10) находим

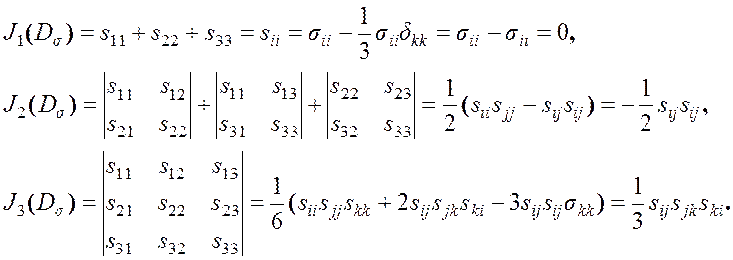
Интенсивностью напряжений называют величину, пропорциональную квадратному корню из второго инварианта девиатора напряжений, взятого со знаком «минус».

В зависимости от принятого коэффициента пропорциональности различают понятия интенсивности нормальных напряжений или просто интенсивности напряжений

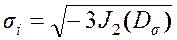
и интенсивность касательных напряжений

.

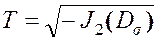Формулу интенсивности напряжений можно выразить через компоненты тензора напряжений

.

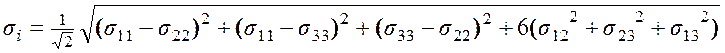Для частного случая одноосного напряженного состояния имеем .

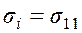3 ФУНДАМЕНТАЛЬНЫЕ ЗАКОНЫ МЕХАНИКИ

3.1 ТЕОРЕМА ПЕРЕНОСА

Рассматривается некоторый объем , состоящий из одних и тех же частиц сплошной среды, перемещающихся в пространстве. Пусть в этом объеме определена плотность некоторой физической характеристики, которая. в свою очередь, определяется интегралом по подвижному объему .

.

Определим скорость изменения этой величины по времени

.

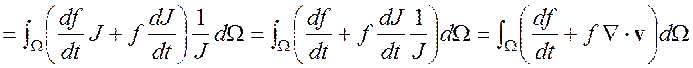Используем это теорему при выводе уравнений из фундаментальных законов.

3.2 ЗАКОН СОХРАНЕНИЯ МАССЫ

Одним из первых опытно установленных законов природы, верный в определенном приближении, можно считать фундаментальный закон механики Ньютона – закон сохранения массы. Пусть плотность массы и — произвольный объем одних и тех же материальных частиц, перемещающихся в пространстве так. Тогда масса

.

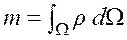Закон сохранения выражается в том, что скорость изменения массы в каждый момент времени равна нулю. Применяя теорему переноса, получаем

.

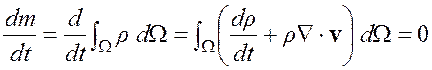Отсюда в силу произвольности объема имеем

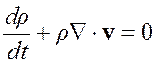. (3.1)

3.3 ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА

Следующим фундаментальным законом является закон о сохранении количества движения или импульса: скорость изменения количества движения произвольного объема, состоящего из одних и тех же материальных частиц. равна сумме поверхностных и массовых сил.

.

Выражая вектор напряжения через тензор напряжения, применяя теорему переноса и формулу Гаусса-Остроградского, получаем

.

Но в силу произвольности объема и соотношения (3.1) имеем

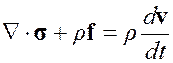. (3.2)

Полученные уравнения называются уравнениями движения сплошной среды.

3.4 ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

В том случае, когда мы пренебрегаем внутренним моментом количества движения и моментным взаимодействием частиц. справедлив закон сохранения количества движения: скорость изменения момента количества движения равна моменту массовых и поверхностных сил

.

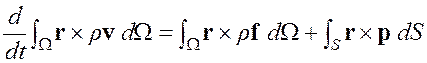Совершенно аналогично выражаем вектор напряжения через тензор напряжения, применяя теорему переноса и формулу Гаусса-Остроградского, получаем

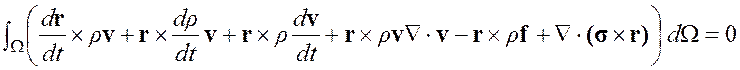
После некоторых преобразований, и учета (3.1) – (3.2), получаем

,

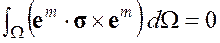что в силу произвольности объема дает

.

Это соотношение можно переписать в виде

,

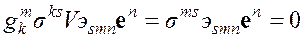где — символы Леви-Чевитта. Из этих соотношений вытекает

. (3.3)

Таким образом, получаем, что в классическом случае тензор напряжений симметричен.

4 ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. Поле скоростей в эйлеровом пространстве имеет вид

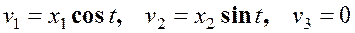. (4.1)

Найти: тензор скоростей деформаций; изменение плотности в процессе движения; закон движения; вектор перемещения как функцию лагранжевых коородинат ; тензор деформаций .

Запишем (4.1) в виде системы дифференциальных уравнений в эйлеровых координатах

,

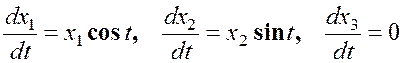и интегрируем

.

Постоянные интегрирования находим из начальных условий, показывающих, что в наячальный момент эйлеровы и лагранжевы координаты совпадают

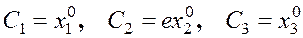
А общее решение принимает вид

.
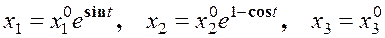