– Кинематические «парадоксы» специальной теории относительности

Обозначим u-скорость частицы. По определению

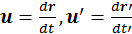. (1.4.2)

Тогда для проекции скоростей получим:

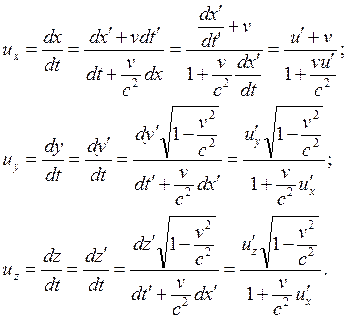(1.4.3)

Эти выражения есть преобразования Лоренца для скоростей. Убедимся теперь, что в нерелятивистском приближении мы получим вновь преобразования Галилея, пренебрегая выражением :

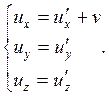(1.4.4)

Перейдем теперь к преобразованиям Лоренца для углов. Рассмотрим случай больших скоростей. Пусть в системе частица покоится (рис. 1.13). Тогда скорость в проекциях на оси и можно представить как:

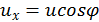
В K′ системе:

Найдем :

Рис.5

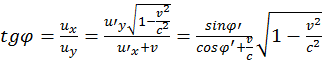
Чтобы избавиться от функции tgφ, запишем:

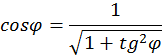
Затем вспомним, что 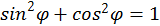. В конечном итоге получим:

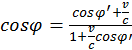(1.4.5)

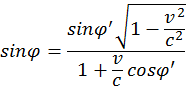
Это и будут преобразования Лоренца для углов.

§ 1.5. Кинематические «парадоксы» специальной теории относительности

Парадокс — явление, которое не укладывается в рамках обыденных представлений.

Таких парадоксов существует несколько:

1. Эффект прожектора;

2. Аберрация света;

3. Парадокс близнецов;

4. Сокращение продольных размеров движущихся тел;

5. Поперечный эффект Доплера.

В этом параграфе мы рассмотрим только первые четыре парадокса. Последний мы рассмотрим значительно позднее.

1. Эффект прожектора

Пример: Пусть в «ракете», летящей со скоростью порядка скорости света человек светит («фонариком») в направлении перпендикулярном движению «ракеты» (рис.6 ).

ψ′=900

Скорость v очень большая. Луч света пойдет практически параллельно направлению движения ракеты. Воспользуемся преобразованием Лоренца для углов:

Рис. 6

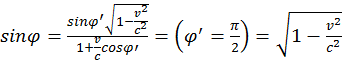
Если 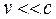, то ничего необычного наблюдаться не будет. Если же 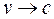, то из предыдущего следует, что

Эффект прожектора очень ярко наблюдается в современных ускорителях, где скорости электронов достигают скоростей порядка скорости света.

В таких ускорителях при излучение электрона происходит практически по касательной к траектории, причем угол раствора для излучения электрона составляет секунды (рис.7).

Рис.7

Наташа

Автор

Наташа — контент-маркетолог и блогер, но все это не мешает ей оставаться адекватным человеком. Верит во все цвета радуги и не верит в теорию всемирного заговора. Увлекается «нефрохиромантией» и тайно мечтает воссоздать дома Александрийскую библиотеку.