Кинематический инвариант
Это и есть лоренцевская формула преобразования времени при переходе в движущуюся систему координат.
Итак, полный комплект преобразований Лоренца при выбранной нами ранее конфигурации координатных осей выглядит следующим образом: 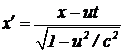 ;
;
![]() ; (3)
; (3)
![]() ;
;
.
Преобразуются только координата x и время t. Поперечные координаты не преобразуются.
Задача 1. Используя систему уравнений (3), получите преобразования Лоренца для перехода от штрихованных координат и времени к нештрихованным.
2.3 Формула сложения скоростей
Допустим, имеется движущаяся частица (или тело), и в некоторой системе отсчета ее скорость равна v. Задача состоит в том, чтобы определить скорость этой частицы в системе отсчета, равномерно движущейся относительно исходной вдоль оси OX, со скоростью u. Координаты и время, измеренные в исходной системе отсчета будем обозначать нештрихованными буквами, а в движущейся — штрихованными.
По определению,
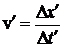 . (4)
. (4)
Приращения ![]() и
и ![]() определим, пользуясь формулами преобразования Лоренца (3):
определим, пользуясь формулами преобразования Лоренца (3): 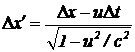 , (5)
, (5) 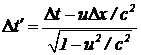 . (6)
. (6)
Подставим эти выражения в определение (4). Тогда 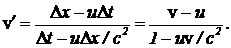 (7)
(7)
Для примера применим данное правило сложения скоростей к распространяющемуся свету. Имеем v=c, тогда
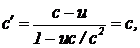 (8)
(8)
что согласуется с фактом независимости скорости света от выбора системы отсчета.
2.4 Решение задач
Задача 2. Спустя 10-8 с после распада нейтрона (на протон, электрон и нейтрино), нейтрино оказалось на расстоянии 3 м от места рождения. На каком расстоянии от электрона (с точки зрения электрона), летящего в том же направлении в три раза медленнее, находится нейтрино, если при распаде они образуются одновременно?
Задача 3. Две частицы летят навстречу друг другу с равными скоростями, составляющими половину скорости света. Чему равна относительная скорость частиц?
Задача 4. Чему равна относительная скорость двух инерциальных систем отсчета, если в одной из них скорость частицы равна c/3, а в другой c/2.
Задача 5. В лабораторной системе отсчета одна из частиц покоится, а другая удаляется от нее со скоростью v. Определите скорость такой системы отсчета (относительно исходной), в которой частицы бы двигались в противоположных направлениях с равными по модулю скоростями.
3. Домашнее задание
3.2 Решение задач
Задача 1. В теории относительности важной характеристикой события, произошедшего в точке с координатами x, y, z в момент времени t является интервал, который определяется как 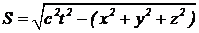 . Определите интервал для этого же события в системе отсчета, с координатными осями, параллельными координатным осям исходной системы отсчета, движущейся в направлении оси OX со скоростью u относительно исходной, если в момент времени t=0 начала координат обеих систем отсчета совпадали. Из результата сделайте вывод.
. Определите интервал для этого же события в системе отсчета, с координатными осями, параллельными координатным осям исходной системы отсчета, движущейся в направлении оси OX со скоростью u относительно исходной, если в момент времени t=0 начала координат обеих систем отсчета совпадали. Из результата сделайте вывод.
Задача 2[51.5]. В некоторой системе отсчета две частицы движутся в противоположных направлениях со скоростями, модули которых равны 0,6×c. Чему равна относительная скорость частиц?
Задача 3. В некоторой системе отсчета частица движется со скоростью, проекции которой равны vx, vy, vz, Чему равны проекции скорости в системе отсчета, с координатными осями, параллельными координатным осям исходной системы отсчета, движущейся в направлении оси OX со скоростью u относительно исходной?
Ответ: 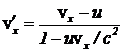 ;
; 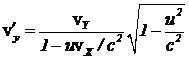 ;
; 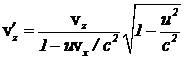 .
.
занятие 1.5.4
кинематический инвариант. решение задач
1.1 Теоретические вопросы
а) Выступление учащегося о преобразовании пространственных координат.
б) Выступление учащегося о преобразовании времени.
в) Выступление учащегося о правиле сложения скоростей.
1.2 Обсуждение задачи 1 домашнего задания
Вопрос 1. Какой можно сделать вывод из решения задачи о свойствах интервала?
2. Интервал
Могло показаться, что в теории относительности, кроме скорости света, нет величин, неизменных при переходах от системы к системе отсчета. Даже ранее казавшиеся незыблемыми величины — промежутки времени и длины — по теории относительности в различных системах отсчета выглядят по-разному. Это обусловлено тем, что в теории относительности пространство и время выступают сторонами одной и той же сущности — четырехмерного многообразия — пространства-времени.
В теории относительности имеется ряд величин, измерения которых в разных системах отсчета дают одни и те же значения. О таких величинах говорят, что они инвариантны (неизменны) при переходах из одной системы отсчета в другую. Одна из них — интервал. Определение интервала между событием, произошедшим в начале координат в начальный момент времени дано в задаче 1 домашнего задания. Интервал — всегда характеристика соотношения между двумя событиями. Сформулируем более общее определение, годное для произвольных двух событий. Пусть в некоторой системе отсчета на расстоянии 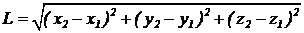 друг от друга через время t=t2-t1 произошли два события. Интервалом между этими двумя событиями называется величина S, определяемая так:
друг от друга через время t=t2-t1 произошли два события. Интервалом между этими двумя событиями называется величина S, определяемая так: 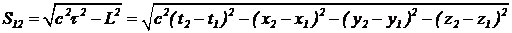 . (10)
. (10)
Интервал в четырехмерном мире играет ту же роль, что и длина в трехмерном — что-то вроде расстояния между двумя событиями. Это длина разности четырехмерных радиус-векторов двух событий.
Среди инвариантных величин относительно преобразований Лоренца, кроме интервала, можно назвать еще заряд тела. Заряд тела в любой системе отсчета один и тот же.
Задача 1. Через точку A и точку B, находящиеся на расстоянии L друг от друга прошел световой импульс. Определите интервал между прохождениями импульса точек A и B.
Задача 2. Через точку A и точку B, находящиеся на расстоянии L друг от друга пролетела частица со скоростью v. Определите интервал между прохождениями частицы точек A и B.
Инвариантность интервала относительно преобразований Лоренца широко эксплуатируется в теории относительности. Так, преобразования Лоренца можно получить из факта инвариантности интервала.
Задача 3. Собственное время жизни частицы равно t0. Используя инвариантность интервала относительно преобразований Лоренца, получите формулу расчета среднего времени жизни частицы в лабораторной системе отсчета, в которой частица движется со скоростью v.
Указание: совместите начало координат движущейся системы отсчета с частицей и предварительно установите соответствие между временем жизни и координатой частицы в лабораторной системе отсчета.
Решение. Пусть частица находится в начале координат движущейся системы отсчета. Пусть t`=0 — момент рождения частицы, тогда t`=t0 — момент распада частицы. В системе отсчета, связанной с частицей, интервал между рождением и распадом равен ct0. В лабораторной системе отсчета координата точки, в которой частица распалась, равна vt, где t — время жизни в лабораторной системе отсчета. Поэтому интервал между рождением и распадом частицы в лабораторной системе отсчета равен 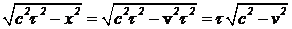 . Из инвариантности интервала между рождением и распадом следует
. Из инвариантности интервала между рождением и распадом следует
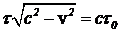 . (11)
. (11)
Откуда получаем
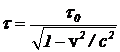 , (12)
, (12)
что совпадает с ранее полученным результатом.


