Комбинационный принцип ритца

.

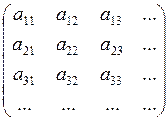В подобной же схеме можно расположить и другие величины, связанные с переходом .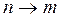

Теперь возникает естественный вопрос: как же обращаться с такими таблицами при вычислениях?

Здесь необходимо познакомиться со следующим замечанием Гейзенберга: перемножая два колебания

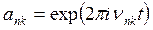и ,

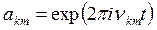мы благодаря комбинационному принципу Ритца получаем

,

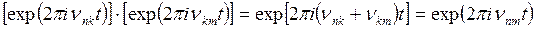т. е. колебание из той же самой таблицы, так что правило образования произведения позволяет просто перейти к другому месту квадратной таблицы в согласии с правилом обозначения мест.

Теперь можно определить произведение двух таких таблиц, причем так, что это произведение снова окажется квадратной таблицей того же самого типа.

Правило умножения, выведенное Гейзенбергом только из результатов эксперимента, гласит

.

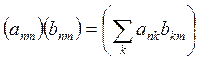Борн и Йордан заметили, что это правило умножения совпадает с другим, которое известно в математике как правило образования произведения двух матриц, которые изучаются в теории линейных преобразований и теории определителей. Поэтому квадратные таблицы Гейзенберга можно рассматривать как бесконечные матрицы и действовать с ними по известным правилам теории матриц.

Центральным пунктом матричной механики является принцип, согласно которому с каждой физической величиной связана представляющая её матрица описанного выше типа.

Можно построить матрицу координаты, матрицу импульса и т. д., а затем действовать с этими матрицами практически точно так, как мы привыкли действовать с координатами, импульсами и т. д. в классической механике.

Сразу же сделаем важное замечание. Между матричной и классической механикой имеется одно существенное различие, а именно: когда в качестве координат и импульсов оперируют матрицами, произведение этих величин уже не коммутативно, т. е. не выполняется, как это было в классической механике, соотношение

.

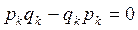Значение такого коммутатора, как показывает теория, не произвольно. Выражение в левой части, образованное парой канонически сопряженных переменных 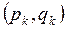, может иметь тоько одну определенную величину:

.

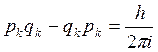Эти перестановочные соотношения (Борн и Йордан, 1925 г.) играют здесь роль квантовых условий теории Бора.

Заметим, что аналогичные перестановочные соотношения естественным образом появляются в волновой механике, к изучению которой мы и перейдем, обратив, в заключение, внимание на то, что фундаментальная идея, лежащая в основе работы Гейзенберга была оригинальным образом разработана в 1925 г. также Дираком.

Приложение. Комбинационный принцип Ритца.

Суть комбинационного принципа состоит в следующем.

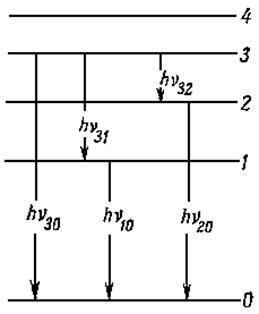Пусть атом находится в третьем возбужденном состоянии.

Из этого состояния атом может вернуться непосредственно в

основное, испустив квант энергии частотой ,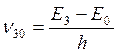

либо, например, перейти в первое возбужденное состояние,

испустив квант энергии , а уже затем – в основное, что

соответствует частоте излучения , и т. д.

Поскольку в совокупности испущенная энергия остается

одной и той же, то частоты излучения должны подчиняться

следующему соотношению:

.

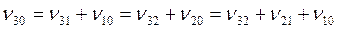В этом и состоит комбинационный принцип, который

должен выполняться при всех обстоятельствах и может

использоваться для экспериментальной проверки теории.

Исторически же все сложилось наоборот – комбинационный принцип был выдвинут Ритцем на основе анализа накопившихся к тому времени спектроскопических данных еще за восемь лет до создания боровской теории атома.

Не следует, однако, думать, что все возможные “комбинационные линии” доступны наблюдению. Некоторые из них могут не обладать сколько-нибудь заметной интенсивностью.

Волновая механика.

Совершенно независимо от рассмотренного выше подхода, попытки решить проблему строения атома были предприняты на основе представлений о волновых свойствах материи.

Согласно гипотезе де-Бройля, каждой частице соответствует волна, причем длина этой волны в случае прямолинейного движения частицы, как мы знаем, связана с импульсом последней соотношением

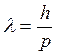. (в 1)

Совершенно логичной представляется попытка расширить теорию, применяя волновую идею к атому, т. е. рассмотреть поведение электрона, движущегося вокруг ядра с волновой точки зрения. В таком случае атом следовало представлять как волновое движение вокруг выделенной в пространстве точки – атомного ядра.

Т. о., задача теории состояла в нахождении закона этого движения.

Попытаемся воспроизвести рассуждения, которые в свое время привели к установлению волнового уравнения – дифференциального уравнения, выражающего закон волнового движения в атоме.

Вообще говоря, это не более, чем предположение, следующее из аналогии с другими колебательными процессами, что основной закон интересующего нас движения будет выражен дифференциальным уравнением.

Более того, волновое уравнение нельзя вывести строго логически – формальные шаги, ведущие к нему, являются, в сущности, остроумными догадками. Критерием правильности полученного результата служит, как всегда, эксперимент.

Проиллюстрировать подход к решению поставленной задачи могут следующие рассуждения:

поскольку плоские волны описывают движение свободной частицы, то они должны быть частным решением искомого уравнения;

нам уже известно волновое уравнение, решением которого являются плоские волны, но оно ”недостаточно”, поскольку справедливо для волновых процессов, но не отражает корпускулярных свойств волны-частицы.

претендуя на общность, уравнение должно содержать только фундаментальные константы;

уравнение должно быть линейным и однородным, тогда волна, являющаяся его решением, удовлетворяет принципу суперпозиции, характерному для волновых процессов в общем виде.

искомое уравнение должно быть дифференциальным уравнением первого порядка относительно времени, поскольку именно в этом случае знание волновой функции в данный начальный момент времени оказывается достаточным для определения её эволюции.

Важно отметить, что предсказания развиваемой теории должны совпадать с предсказаниями классической механики в области, где справедлива последняя. Следовательно, искомое уравнение должно удовлетворять принципу соответствия, что может быть обеспечено, если оно будет обладать формальным сходством с некоторыми уравнениями классической механики.

Уравнение Шредингера.

Уравнение, получившее его имя, Шредингер установил исходя из оптико-механической аналогии. Указанная аналогия заключается в формальном сходстве уравнений оптики, описывающих ход световых лучей, с уравнениями механики, определяющими траектории частиц.

Подчеркнем еще раз, что изложенные ниже рассуждения не имеют доказательной силы и не могут рассматриваться как вывод уравнения Шредингера. Их целью является пояснить, каким образом можно было прийти к установлению этого уравнения.

Начнем с рассмотрения движения свободной частицы.

Связанную с ней волну мы описываем волновой функцией координаты и времени вида:

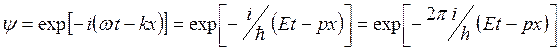. (в 2)

Здесь, как обычно, и циклическая частота и волновое число, которые, согласно де-Бройлю, связаны с энергией и импульсом уравнениями:

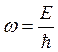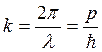; . (в 3)

Взяв производные от (в 2) по и , мы обнаруживаем, что

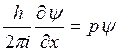(в 4)

и

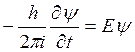. (в 5)

Полученные таким образом уравнения можно “прочесть наоборот”, считая, что даны дифференциальные уравнения, а требуется найти их решение.

Пусть частица движется по прямой линии и допустимы все значения между и , тогда решением уравнений (в 4) и (в 5) будет функция (в 2).

В случае, когда частица движется по окружности радиусом , дело обстоит иначе. Если мы обозначим через координату точки, измеряемую по дуге от фиксированной точки окружности, то может принимать только значения от до 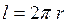. Перемещение частицы на возвращает её в точку с координатой .

Функция должна быть однозначной на окружности, поэтому перемещение из точки с координатой , равное 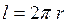, не должно менять значения функции.

Теперь общее решение уравнения (в 4) есть функция

.

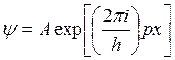При изменении координаты на длину эта функция умножается на

.

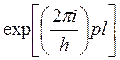Для того, чтобы функция была “собственной функцией”, этот множитель должен равняться единице:

,

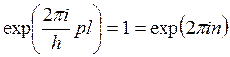или

.

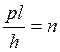
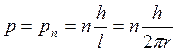Это означает, что в случае кругового движения уравнение (в 4) обладает допустимыми решениями не для всех значений , а только для дискретных “собственных значений”:

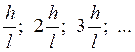
Формализм, который Шредингер (1926 г.) счел подходящим для волновой теории атома, базируется на следующем правиле.

В нерелятивистской классической механике энергия свободной частицы может быть выражена через её импульс посредством уравнения

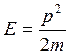, или . (*)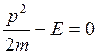

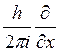Запишем импульс как оператор, заменив на , причем оператор, соответствующий , получается повторением дифференцирования, а именно

.

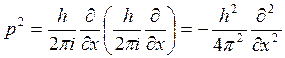Энергетический спектр частицы мы сможем найти, составив дифференциальное уравнение по аналогии с (*)

,

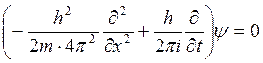т. е. подействовав оператором энергии на волновую функцию .

Последнее уравнение можно переписать в форме:

.

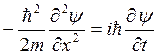Это уравнение легко распространяется на трехмерный случай.

Т. о., дифференциальное уравнение, решением которого является волновая функция 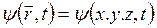, описывающая свободное движение частицы, имеет вид:

, (**)

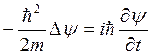где 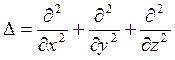– оператор Лапласа.

Написанное уравнение называется уравнением Шредингера.

Если частица движется в силовом поле, характеризуемом потенциальной энергией 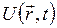, то уравнение классической механики, определяющее энергию частицы, записывается как

.

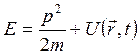В свою очередь, уравнение Шредингера приобретает вид:

.

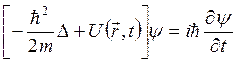Если теперь ввести, как это принято, оператор Гамильтона (гамильтониан):

,

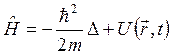то уравнение Шредингера примет вид:

.

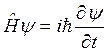Таким образом, мы вооружены формализмом, позволяющим приступить к решению любой механической задачи. Решить задачу – означает найти для неё однозначное и конечное решение волнового уравнения Шредингера.

Уравнение Шредингера для стационарных состояний.

Если силовое поле, в котором движется частица, постоянно во времени – стационарно , то решение уравнения (**) Шредингера распадается на два независимых сомножителя, один их которых зависит только от пространственных координат, а второй – от времени.

Представим волновую функцию в виде произведения

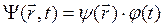(4.11)

и подставим в уравнение Шредингера:

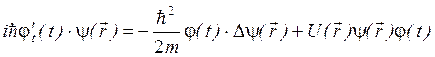(4.12)

Поделим теперь обе части уравнения (4.12) на функцию .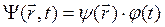

Получаем

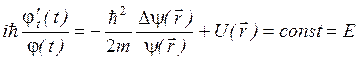. (4.13)

Действительно, левая часть уравнения (4.13) зависит только от времени t, а правая – только от пространственных координат.

Поскольку это равенство справедливо при произвольных значениях независимых переменных, то обе части уравнения можно приравнять константе, называемой константой разделения, которую мы обозначили через .

Т. о., уравнения для пространственной и временной переменных разделяются, в результате чего мы получаем два уравнения.

Первое – уравнение для функции , зависящей только от времени:

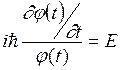. (4.14)

Его решение достаточно легко найти –

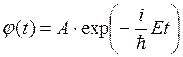(4.15)

Второе уравнение – для координатной части волновой функции принимает вид:

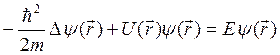(4.16)

или

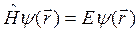. (4.17)

Уравнение (4.17) и есть стационарное уравнение Шредингера.

В стационарном силовом поле решение уравнения Шредингера (полная волновая функция), согласно (4.11) и (4.15), имеет вид:

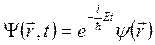. (4.18)

Уравнение Шредингера является основным уравнением нерелятивистской квантовой механики. Оно не может быть выведено их других соотношений. Его следует рассматривать как исходное основное предположение, справедливость которого обосновывается тем, что все вытекающие из решений уравнения Шредингера следствия согласуются с результатами опыта.

Волновая функция.

Итак, в основу квантово-механического описания физической системы положено утверждение, что состояние системы может быть описано определенной, вообще говоря, комплексной функцией координат и времени 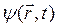, называемой волновой функцией системы.

Волновая функция есть максимально полное допустимое описание состояния частицы или системы частиц.

Если волновая функция известна в некоторый начальный момент времени, то по самому смыслу понятия полного описания состояния она тем самым в принципе определена и во все будущие моменты времени.

Волновая функция должна удовлетворять совокупности требований, которые носят название стандартных условий.

В соответствии со смыслом, заложенным в волновой функции, она должна быть однозначной непрерывной и конечной, за исключением, может быть, особых точек. Кроме того, волновая функция должна иметь непрерывную и конечную производную.

Квадрат модуля волновой функции пропорционален вероятности того, что произведенное над системой измерение обнаружит ее в окрестности координаты ,

Знание волновой функции позволяет в принципе вычислить вероятности различных результатов, т. е. не только измерения координат, но и всякого вообще измерения.

При этом все вероятности определяются выражениями, билинейными по и .

Например,

, (*)

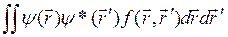где 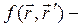функция, вообще говоря, зависящая от рода и результата измерения.

Сумма вероятностей всех возможных значений координат системы должна быть, по определению, равной единице. Поэтому нужно, чтобы результат интегрирования по всему пространству был равен единице:

.

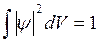Это равенство представляет собой условие нормировки волновых функций.

Вообще говоря, интеграл от может расходиться. Тогда функция не может быть нормирована условием . В таких случаях уже не определяет абсолютные значения вероятности координат, но, тем не менее, отношение квадратов модулей волновой функции в двух различных точках пространства определяет относительную вероятность соответствующих значений координат.

Физический смысл волновой функции определяет статистический характер квантовой механики.

Знание волновой функции не позволяет определить местонахождение частицы в пространстве или траекторию, по которой движется частица. Волновая функция дает возможность предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства.

Однако, это никоим образом не означает, что квантовая механика дает менее точное и исчерпывающее описание движения частицы, чем классическая механика, которая, казалось бы, с любой заданной точностью определяет местоположение и скорость частицы в каждый момент времени.

Квантовая механика не определяет лишь то, чего нет на самом деле, поскольку понятия определенного местоположения и траектории в применении к микрочастицам вообще теряют смысл.

Приложение.

Об интерпретации волновой функции.

В 2030х годах прошлого века разгорелся спор между Н. Бором и А. Эйнштейном о вероятностной интерпретации волновой функции и соотношении неопределенностей.

Во время работы V Сольвеевского конгресса А. Эйнштейн каждое утро предлагал очередное доказательство нарушения соотношения неопределенностей в придуманном им опыте, а вечером Н. Бор снова и снова показывал, что при более тщательном рассмотрении правильность соотношения неопределенностей подтверждается.

А. Эйнштейн так и не смог найти слабого места в логике построения квантовой механике, однако, по его убеждению, такая точка зрения не могла быть окончательным решением. Свою позицию он резюмировал ставшей весьма известной фразой: “Господь Бог не играет в кости”.

Нужно ли искать другую интерпретацию квантовой механики?

Чтобы ответить на этот вопрос необходимо, подчеркнуть особенности, присущие квантовой механике, и принципиально отличающие используемые ею подходы к описанию физических систем от тех, которыми оперирует классическая механика, необходимо отметить, что волновая функция представляет собой не физическое поле, а поле информационное.

Если отожествлять волновую функцию с физическим полем, например, моделировать посредством нее частицу, то можно получить совершеннейшую бессмыслицу. Если же учесть, что волновая функция – это волна информации, то получаемые результаты оказываются совершенно естественными.