Кручение стержня круглого поперечного сечения
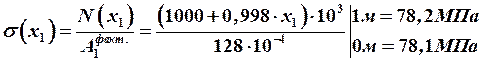
![]()
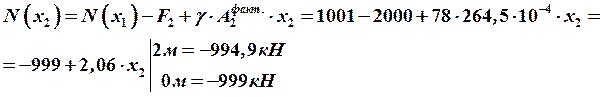
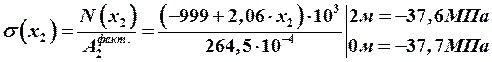
![]()
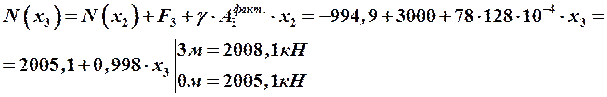
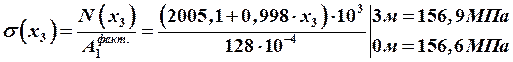
Строим эпюры продольных сил и нормальных напряжений.
4. Определяем полную абсолютную деформацию стержня.
Перемещение нижнего конца стержня складывается из деформаций его участков
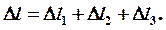
Деформации каждого участка стержня, находящегося под действием внешних сил и сил тяжести, определяем по закону Гука.
Деформация участка длиной а получит деформацию от действия собственного веса ![]() участка длиной а и внешней силы
участка длиной а и внешней силы ![]()
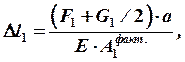
где 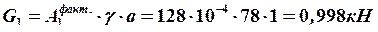 – собственный вес первого участка.
– собственный вес первого участка.
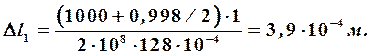
На первом участке стержень удлиняется.
Деформация участка длиной b будет складываться из деформаций от действия внешней силы ![]() (сила тяжести первого участка по отношению ко второму будет выступать в данном случае в виде внешней силы), внешних сил
(сила тяжести первого участка по отношению ко второму будет выступать в данном случае в виде внешней силы), внешних сил ![]() ,
, ![]() а также от действия собственного веса
а также от действия собственного веса ![]() .
.
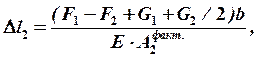
где 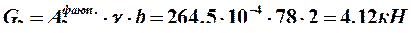 – собственный вес второго участка.
– собственный вес второго участка.
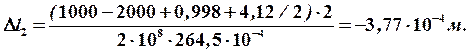
На втором участке стержень также удлиняется.
Деформация участка длиной с будет складываться из деформации от действия внешних сил ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и от действия собственного веса
и от действия собственного веса ![]() .
.
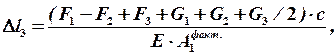
где 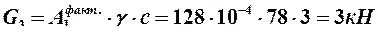 – собственный вес третьего участка.
– собственный вес третьего участка.
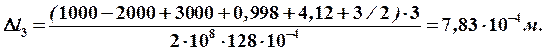
На третьем участке стержень получит удлинение.
Полное абсолютное удлинение стержня
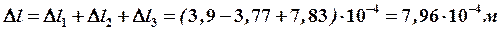
Задание 2 Кручение стержня круглого поперечного сечения
1. Вычерчиваем расчетную схему вала с приложенными внешними моментами 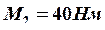 ,
, 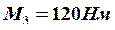 ,
, 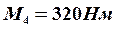 , передаваемыми ведомыми шкивами (рис. 18). (
, передаваемыми ведомыми шкивами (рис. 18). (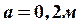 ,
,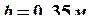 ,
,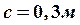 )
)
2. Определяем крутящий момент ![]() на ведущем шкиве. Учитывая, что вал вращается равномерно, составляем уравнение равновесия:
на ведущем шкиве. Учитывая, что вал вращается равномерно, составляем уравнение равновесия:
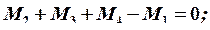
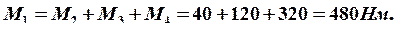
3. Строим эпюру крутящих моментов. Для определения величины крутящих моментов используется метод сечений.
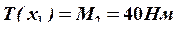 ;
;
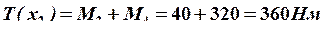 ;
;
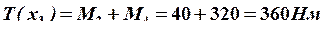 ;
;
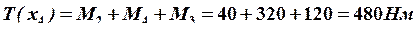 ;
;
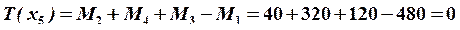 .
.
Строим эпюру крутящих моментов (рис. 18, а).
4. Определяем рациональное расположение шкивов на валу.
Рациональное расположение шкивов на валу, такое, при котором крутящие моменты будут распределены наиболее равномерно по длине вала и с наименьшими значениями.

Рис. 18
При этом ведущий шкив должен располагаться как можно ближе к центру длины вала. В результате такого расположения шкивов обеспечивается наименьший расход материала (уменьшается площадь поперечного сечения).
Рассмотрим вариант, представленный на рис. 18, б.
Определяем значения крутящих моментов ![]() , для данного расположения шкивов:
, для данного расположения шкивов:
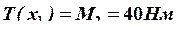 ;
;
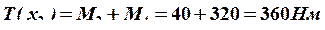 ;
;
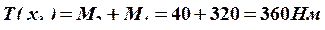 ;
;
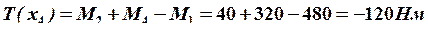 ;
;
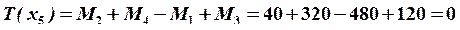 .
.
Строим эпюру крутящих моментов для данного варианта.
Рассмотрим вариант, представленный на рис. 18, в.
Определяем значения крутящих моментов ![]() , для данного расположения шкивов:
, для данного расположения шкивов:
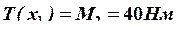 ;
;
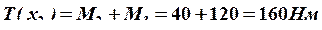 ;
;
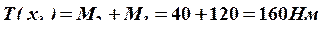 ;
;
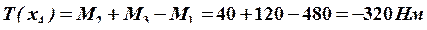 ;
;
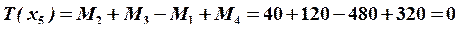 .
.
Строим эпюру крутящих моментов для данного варианта.
Из рассмотренных вариантов, наиболее предпочтительным будет являться схема расположения шкивов, представленная на рис. 18, в, т. к. максимальный крутящий момент ![]() имеет наименьшее значение из рассмотренных ранее вариантов.
имеет наименьшее значение из рассмотренных ранее вариантов.
5. По условию прочности рассчитываем диаметр вала в опасном сечении:
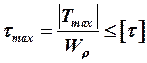 .
.
Определяем необходимый полярный момент сопротивления (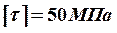 )
)
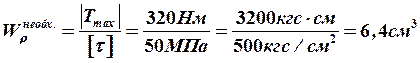 .
.
Для сплошного круглого сечения: .
Подбираем диаметр вала:
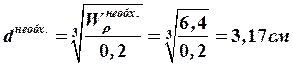 .
.
Исходя из заданных по условию диаметров, принимаем 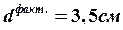 .
.
Определяем фактический полярный момент сопротивления
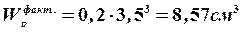 .
.
Определяем максимальное касательное напряжение:
,
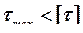 , что соответствует условию прочности.
, что соответствует условию прочности.
6. Определяем деформации в характерных сечениях вала
.
Произведение ![]() называется жесткостью при кручении.
называется жесткостью при кручении.
Определяем полярный момент инерции сечения:
.
Определяем жёсткость вала:
.
Вычисляем относительные углы закручивания ![]() .
.
Учитывая, что вал вращается равномерно, расчет углов закручивания делают относительно сечения, где установлен ведущий шкив, т. е. ![]() .
.
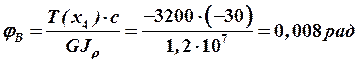 ;
;
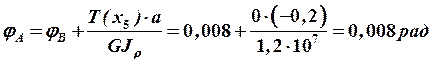 ;
;
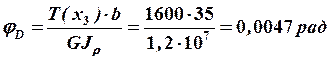 ;
;
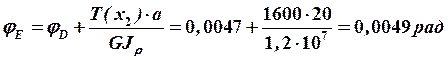 ;
;
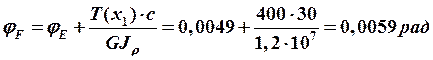 .
.
Строим эпюру относительных углов закручивания ![]() .
.
Делаем проверку по углам закручивания.
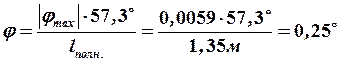 ,
, 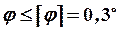 .
.
Задание 3 Расчет на прочность при изгибе
1. Вычерчиваем расчетную схему балки с заданными нагрузками
(рис. 19), соблюдая масштаб длины участков. Проставляем числовые значения.
2. Изображаем опорные реакции, возникающие в опорах балки. Вычисляем их величину:
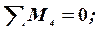 ;
;
|
Рис. 19 Расчетная схема, эпюры и |
Дано:
|
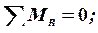
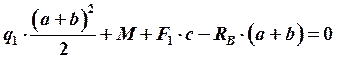 ;
;
.
Проверка:
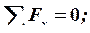
3. Применяя метод сквозного разреза, разбиваем схему балки на силовые участки (в нашем случае их – 3). Соблюдая правило знаков, определяем значения и ![]() в сечениях.
в сечениях.
Вычисляем значения и ![]() на каждом участке:
на каждом участке:
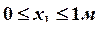
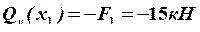
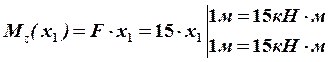
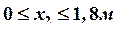
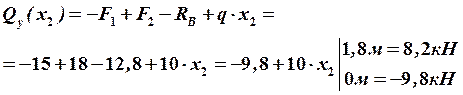
Обращаем внимание на то, что наклонная прямая, ограничивающая эпюру 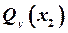 , проходит через 0. Это означает, что на эпюре
, проходит через 0. Это означает, что на эпюре 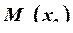 надо искать точку перегиба.
надо искать точку перегиба.


