Квантование энергии

После подстановки выражения (22) в формулу (20), находим
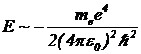. (23)
Разумеется, это оценка по порядку величины. Но случайно оказалось, что данное значение прекрасно согласуется с экспериментальными данными по ионизации атома водорода: E»13,6 эВ.

4. Домашнее задание

4.1 Теоретический материал

Проработать материал занятия по пособию, по своим конспектам. Дополнительно по учебнику “Физика 11” под ред. А. А.Пинского. §71.

4.2 Решение задач

Задача 1. Атом в возбужденном состоянии живет в среднем время Dt. После этого он переходит в состояние с меньшей энергией, излучая фотон. Покажите, что неопределенность энергии фотона DE связана со временем жизни атома в возбужденном состоянии соотношением DEDt~ћ.

Задача 2. Используя принцип неопределенностей, оцените энергию основного состояния гармонического осциллятора массы m и коэффициентом жесткости k. Сравните полученный результат с формулой Планка.

занятие 2.1.10

решение задач. квантование энергии

1.2 Контрольные вопросы

1.2.1 Как связаны между собой частота волны амплитуды вероятности частицы и ее энергия?

1.2.2 Как связаны между собой длина волны амплитуды вероятности частицы и ее импульс?

1.2.3 Как выражается энергия свободной частицы через волновое число амплитуды вероятности?

1.2.4 О неопределенностях каких физических величин говорит принцип неопределенностей? Сформулируйте принцип неопределенностей.

1.2.5 Какие экспериментальные данные говорят о том, что при попытке определить положение частицы, имеющей до измерений определенное значение импульса, его определенность исчезает?

1.2.6 Поясните утверждение о том, что попытка локализации частицы в очень малой области пространства, связана с необходимостью совершения работы.

1.2.7 В чем состоят аргументы утверждения, что в состоянии, описываемом пространственно локализованным цугом волны амплитуды вероятностей, импульс частицы неопределен?

1.2.8 Проводят два эксперимента. Через узкую щель пропускают пучок фотонов. Затем, на той же щели, то же самое делают с пучком электронов, с тем же импульсом. Чем будут отличаться дифракционные картины?

1.2.9 Как связаны между собой время жизни атома в возбужденном состоянии и энергия излучаемого им фотона? Почему?

2. решение задач

Задача 1. В эффекте Мессбауэра используется рентгеновское излучение возбужденных ядер изотопа железа 57Fe. Причем оказывается, что ширина линии излучения равна всего 10—5 эВ. Чему равно среднее время жизни возбужденного ядра этого изотопа? Оцените длину цуга волны амплитуды вероятности излучаемого фотона.

Решение. Размытость линии означает величину неопределенности энергии излучаемого фотона или неопределенности энергии возбужденного состояния. В соответствии с принципом неопределенностей DEgDt~ћ, где Dt — время жизни изотопа в возбужденном состоянии. Dt~ћ/DEg=1,05×10-34/10-5×1,6×10-19»6,56×10-11 c. За это время фронт цуга волны амплитуды вероятности уйдет от ядра на 2 см. Это и есть длина цуга волны амплитуды вероятности.

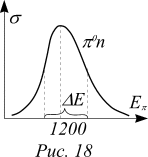Задача 2. В экспериментах по рассеянию отрицательных пионов p— на протонах обнаружили, что при кинетических энергиях налетающих пионов, лежащих в интервале от 130 МэВ до 250 МэВ (на рисунке по оси абсцисс отложены значения полной энергии налетающего пиона), возникает резонансное рождение пары — нейтральный пион и нейтрон. Физики интерпретировали этот факт, как рождение новой частицы (D0-частица), которая после рождения распадается на нейтральный пион и нейтрон. Оцените по приведенным данным среднее время жизни новой частицы.
Дополнительное задание. Оцените инвариантную массу D0-частицы.

Решение. Обратим внимание на то, что рождение пары из распадающейся частицы происходит так же, как рождение фотона при распаде возбужденного состояния атома. Из данных задачи следует, что неопределенность энергии промежуточной частицы равна DE=120 МэВ. Время жизни D0-частицы Dt~ћ/DE=1,05×10-34/1,2×108×1,6×10-19»5,47×10-24 c. За это время фотон успеет переместиться на (~1,6×10-15 м). Расстояние имеет порядок диаметра протона. Столь мало живущие частицы называют резонансами. Единственным средством опознать и определить хотя бы некоторые физические характеристики таких частиц являются эксперименты по исследованию резонансного рассеяния.

Дополнительное задание. Дополнительное задание полезно в качестве повода для повторения релятивистской динамики. Кроме того, оно полезно в общеобразовательном плане. Пусть Ep — полная энергия налетающего пиона, тогда инвариантная масса пары частиц (налетающий пион и протон) равна
.
Раскроем скобки под радикалом и учтем, что . Тогда

Полная энергия пиона равна сумме кинетической энергии и mpc2: Ep=Eкин+ mpc2 Так что уравнение (2) можно переписать так
Mc2= (3)
При расчетах использовалось наиболее вероятное значение кинетической энергии налетающего пиона — 190 МэВ.

Задача 3. В ядре тяжелого водорода протон и нейтрон удерживаются силами ядерного притяжения на расстоянии около 10-15 м. Проведите рассмотрение состояния протона и нейтрона как локализацию частицы приведенной массы в области размером 10-15 м. Используя принцип неопределенностей и учитывая факт устойчивости ядра, сделайте оценку ядерных сил, удерживающих его от распада.

Задача 4. Атомы водорода в молекуле водорода удерживаются ковалентной связью. Физический механизм этой связи можно пояснить с помощью принципа неопределенностей. Электрон в изолированном атоме локализован в области размером 10-10 м. При сближении двух атомов электроны получают возможность перескакивать от атома к атому. При этом размер области их локализации увеличивается, и соответственно неопределенность импульса, а вместе с ней и кинетическая энергия электрона уменьшаются. Используя эту модель, оцените энергию связи атомов в молекуле водорода, если при сближении атомов размер области локализации электронов увеличивается в два раза.

3. Квантование энергии

3.1 Частица в бесконечно глубокой потенциальной яме

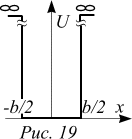У физиков есть очень популярная модель, с помощью которой часто удается понять многие свойства разнообразных физических систем по крайней мере на качественном уровне. Эта модель представляет собой частицу, заключенную между двумя абсолютно непроницаемыми для нее стенками. Математически условия, в которых находится частица, задаются потенциальной ямой с бесконечно высокими стенками. Пусть ширина ямы равна b, а масса частицы m. Потенциальная энергия частицы внутри ямы равна нулю, а вне ямы — бесконечности, т. е. вне ямы частицу застать нельзя. Это и обеспечивает непроницаемость стенки. Наша задача состоит в том, чтобы дать квантовое описание состояния частицы.

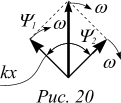Как правило, задача описания состояния оказывается решенной, если удалось найти распределение амплитуды вероятностей в этом состоянии. Найдем распределение. Поскольку частица внутри ямы свободна, распределение амплитуд пребывания частицы в точках внутри ямы должно представлять собой описанную ранее волновую конфигурацию стрелок, вращающихся с угловой скоростью w=E/ћ (E — энергия частицы). Данное распределение обладает одним недостатком — модули всех амплитуд вероятности застать частицу в любой точке ямы одинаковы. Но ведь заранее известно, что амплитуды должны равняться нулю снаружи ямы. Получается, что при переходе через границу ямы амплитуда вероятности должна скачком измениться от конечного значения до нуля. Такое распределение разрывно. Теперь время вспомнить, что распределение амплитуд обладает упругостью и не может изменяться скачком. Поэтому следует искать такое распределение, при котором ход изменения амплитуды вероятности плавно переходит от нуля за пределами к ненулевым значениям внутри ямы.

Указанным требованиям удовлетворяет суперпозиция волн одинакового размаха, бегущих навстречу друг другу. Распределение амплитуд в этом случае представляет собой стоячую волну. Пусть k — волновое число волны амплитуды вероятности, бегущей слева направо, тогда волновое число волны, бегущей справа налево, равно — k. Стрелки обеих волн вращаются в одну и ту же сторону. Разность фаз вращения стрелок в точке x равна 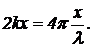Таким образом, если модули волн амплитуд вероятности равны (y1=y2=y0), то, по теореме косинусов, результирующая амплитуда равна
(4)