Квантовая теория теплоемкости двухатомных газов
3. Домашнее задание
3.2 Решение задач
Задача 1. Было установлено, что нейтральные K—мезон (K0) и анти-K—мезон (![]() ) представляют собой равные смеси состояний (в фазе и в противофазе), каждое из которых — самостоятельная частица (KS и KA). Энергии покоя KS и KA отличаются на 0,35 эВ. При столкновениях отрицательного пиона с протоном может рождаться K0. Через какое время этот каон превратится в анти-ка-ноль мезон?
) представляют собой равные смеси состояний (в фазе и в противофазе), каждое из которых — самостоятельная частица (KS и KA). Энергии покоя KS и KA отличаются на 0,35 эВ. При столкновениях отрицательного пиона с протоном может рождаться K0. Через какое время этот каон превратится в анти-ка-ноль мезон?
Эта задача дает пример одного из наиболее удивительных проявлений квантового принципа суперпозиции.
|
|
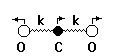
Задача 2. Молекулу углекислого газа можно рассматривать как линейную систему двух связанных осцилляторов с коэффициентом жесткости квазиупругой связи между атомами, равным k»49 кг/с2. а) Чему равны собственные частоты продольных колебаний молекулы углекислого газа?
б) Чему равна колебательная энергия основного состояния молекулы (в эВ)?
в) Каков колебательный энергетический спектр молекулы?
занятие 2.1.12
квантовые поправки к теплоемкости
двухатомных газов
2. Квантовая теория теплоемкости двухатомных газов
2.1 Экспериментальные данные и данные классической теории теплоемкостей
Теплоемкость тела равна отношению бесконечно малого количества теплоты, поглощенного телом, к бесконечно малому приращению температуры, вызванному этим поглощением ![]() Если тепло подводится при постоянном объеме, то работа при этом не совершается, и все тепло идет на нагревание — на увеличение внутренней энергии тела U. Теплоемкость тела в этом процессе подвода теплоты называется теплоемкостью при постоянном объеме. Она равна
Если тепло подводится при постоянном объеме, то работа при этом не совершается, и все тепло идет на нагревание — на увеличение внутренней энергии тела U. Теплоемкость тела в этом процессе подвода теплоты называется теплоемкостью при постоянном объеме. Она равна 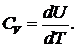 Если тепло подводится при поддержании постоянного давления, то подведенное тепло идет не только на нагревание, но и на совершение работы над внешними телами. При этом повышение температуры оказывается меньшим, чем при подведении тепла при постоянном объеме. Соответственно теплоемкость при постоянном давлении больше теплоемкости при постоянном объеме.
Если тепло подводится при поддержании постоянного давления, то подведенное тепло идет не только на нагревание, но и на совершение работы над внешними телами. При этом повышение температуры оказывается меньшим, чем при подведении тепла при постоянном объеме. Соответственно теплоемкость при постоянном давлении больше теплоемкости при постоянном объеме.
В курсе молекулярной физики 10 кл. было установлено, что в состоянии теплового равновесия на каждую степень свободы поступательного и вращательного движения сложной молекулы газа приходится средняя энергия, равная kБT/2. Внутренняя энергия одного моля одноатомного газа, каждая молекула которого имеет три степени свободы, поэтому равна ![]() (1)
(1)
Внутренняя энергия одного моля двухатомного газа, каждая молекула которого имеет пять степеней свободы, равна
![]() (2)
(2)
Соответственно, молярные теплоемкости при постоянном объеме:
одноатомный — ![]() (3)
(3)
двухатомный — ![]() . (4)
. (4)
Молярные теплоемкости при постоянном давлении на R больше.
В экспериментах измеряется показатель адиабаты g. Он определяется так: 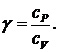 (5)
(5)
Для одноатомного газа он равен ![]() , для двухатомного —
, для двухатомного — ![]() .
.
Экпериментальные исследования показали, что при комнатных температурах показатель адиабаты любого двухатомного газа довольно близок к значению ![]() . Однако при понижении температуры наблюдается увеличение показателя. Так, при температуре ниже 100К показатель водорода становится равным
. Однако при понижении температуры наблюдается увеличение показателя. Так, при температуре ниже 100К показатель водорода становится равным ![]() . Это выглядит так, как будто водород превращается в одноатомный газ. Этот эффект назвали вымерзанием степеней свободы.
. Это выглядит так, как будто водород превращается в одноатомный газ. Этот эффект назвали вымерзанием степеней свободы.
Аномальное поведение показателя адиабаты двухатомного газа наблюдается и при повышении температуры. При высоких температурах, но все-таки более низких, чем температура диссоциации, показатель адиабаты понижается до ![]() , так, как будто у молекулы появились новые степени свободы.
, так, как будто у молекулы появились новые степени свободы.
Перечисленные выше экспериментальные данные, как говорили физики в начале века, являлись легкими облачками на ясном небе классической физики. Никакие классические построения не давали удовлетворительного объяснения температурной зависимости теплоемкости двухатомных газов. Ясное объяснение дала квантовая механика.
2.2 Квантовое объяснение температурной зависимости
теплоемкости
Физическая причина “вымерзания степеней свободы” кроется в квантовании энергии вращения. Энергия вращения может принимать не какие угодно значения, а только вполне определенные. Существуют уровни вращательной энергии. Энергетический спектр вращающейся молекулы имеет вид:
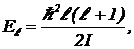 (6)
(6)
где I — момент инерции молекулы, l — натуральное число, которое может принимать значения 1, 2, 3,… Основное состояние имеет энергию![]()
Следующее за ним возбужденное —
Так что разность энергий первых двух уровней равна
![]() (7)
(7)
Для молекулы водорода (см. самостоятельную работу) эта разность оказывается равной
DEH~1,32×10-21 Дж~0,01 эВ.
При взаимодействии с другими молекулами данная молекула не перейдет из основного состояния в возбужденное, если возможная передаваемая энергия при столкновении меньше DEH. Средняя энергия, которой обмениваются молекулы при столкновениях, равна kБT. При низких температурах вращательные уровни не возбуждаются, и вращательная энергия не участвует в теплообмене, т. е. двухатомная молекула ведет себя, как одноатомная. Это и объясняет, почему при низких температурах показатель адиабаты двухатомных газов такой, как у одноатомных. Температура, при которой начинается включение вращательных степеней свободы, называется характеристической температурой. Она определяется соотношением
DE12=kБQ. (8)
Для двухатомных молекул характеристическая температура Q определится так:
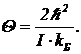 (9)
(9)
Характеристическая температура водорода близка к 100К.
Задача 1. Оцените характеристические температуры основных составных частей атмосферного воздуха — азота и кислорода. О чем говорят полученные вами значения?
Уменьшение показателя адиабаты при высоких температурах связано с особым устройством двухатомных молекул. Молекулу можно деформировать — сблизить атомы. Коэффициенты жесткости k молекул по отношению к этой деформации обычно имеют порядок 10 — 100 кг/с2. Так что молекула, кроме всего, представляет собой осциллятор с собственной частотой 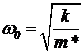 , где — приведенная масса. Например, для водорода оценка дает w0~(1 — 3,5)×1014 c-1. Энергетические уровни осциллятора отстоят друг от друга на ћw0. Это примерно равно 0,23 эВ. При kБT<ћw0 можно считать, что колебательные уровни не возбуждаются и молекула движется, как жесткая гантелька. Но при больших температурах в теплообмен включаются и колебательные степени свободы. Теплоемкость газа повышается. Характеристическая температура для колебательных степеней свободы равна
, где — приведенная масса. Например, для водорода оценка дает w0~(1 — 3,5)×1014 c-1. Энергетические уровни осциллятора отстоят друг от друга на ћw0. Это примерно равно 0,23 эВ. При kБT<ћw0 можно считать, что колебательные уровни не возбуждаются и молекула движется, как жесткая гантелька. Но при больших температурах в теплообмен включаются и колебательные степени свободы. Теплоемкость газа повышается. Характеристическая температура для колебательных степеней свободы равна
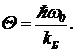 (10)
(10)
Оценка для водорода дает Q~1000 K. Это высокие температуры.
Задача 2. Оцените характеристическую температуру для колебательного движения молекул углекислого газа (воспользуйтесь данными задачи 2 домашнего задания занятия 2.1.11).
3. Домашнее задание
3.2 Решение задач
Задача 1. Молекулы аммиака имеют два стационарных состояния, представляющих собой равную смесь (в фазе и в противофазе) конфигурационных состояний 1 и 2, изображенных на рисунке. Энергии стационарных состояний отличаются на 10-4 эВ. В некоторый момент времени молекула была в состоянии 1. Через сколько времени молекула окажется полностью в состоянии 2?
Указание. Для удобства введите векторное обозначение для состояний: ![]() и
и ![]() — для вращающихся векторов конфигурационных состояний, изображенных на рисунке, и
— для вращающихся векторов конфигурационных состояний, изображенных на рисунке, и ![]() и
и ![]() — для вращающихся векторов стационарных состояний.
— для вращающихся векторов стационарных состояний.