Динамические усилия и волновые процессы в ленте конвейера

.

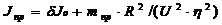Здесь — момент инерций масс, находящихся на валу двигателя; R – радиус барабана; — приведенная масса движущихся частей конвейера и груза : и — погонные массы груза и ленты; L- длина конвейера; — коэффициент, учитывающий, что окружная скорость части движущихся масс меньше, чем скорость ленты ; — масса вращающихся деталей конвейера; кэ= 0,5…0,7 — коэффициент, учитывающий упругое удлинение многопокладочной ленты ( для резинотросовых лент кэ= 0,85…0,95.

Продолжительность пуска конвейера

,

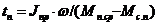где — средний пусковой момент двигателя; — статический момент при пуске, приведенный к валу двигателя:

.

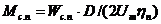Здесь D — диаметр приводного барабана; — передаточное число механизма ;

— КПД в период пуска привода.

Для эффективного торможения тормоз рассчитывают из условия поглощения кинетической энергии движущихся масс конвейера и привода по тормозному моменту:

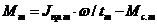, (7.3)

где — приведенный момент движущихся масс конвейера при торможении; — время торможения; — статический момент на валу двигателя при торможении.

Основная литература

Дополнительная литература[10, c.316…318].

Контрольные вопросы:

1.  Назовите эксплуатационные факторы, от которых зависит динамика ленточных конвейеров.

2.  Напишите формулу для определения динамического момента при пуске привода конвейера.

3.  От каких параметров зависит тормозной момент на валу двигателя конвейера?

Лекция 8

Динамические усилия и волновые процессы в ленте конвейера

8.1. Характер распространения волн деформации в ленте

Лента представляет собой систему с распределёнными параметрами. При действии на ленту продольного силового импульса в ней возникают волны деформации, которые распространяются со скоростью

,

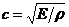где E – модуль продольной упругости ленты; ρ – плотность материала ленты и груза на ленте.

В момент включения привода движение удалённых участков ленты начинается только через некоторый промежуток времени, за который волна от барабана пройдет до рассматриваемого сечения ленты. Уравнение продольных колебании упругой ленты

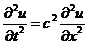, (8.1)

где u – смещение сечения ленты или деформация под действием силового импульса в точке набегания ленты на барабан; x – абсцисса (направлена вдоль ленты).

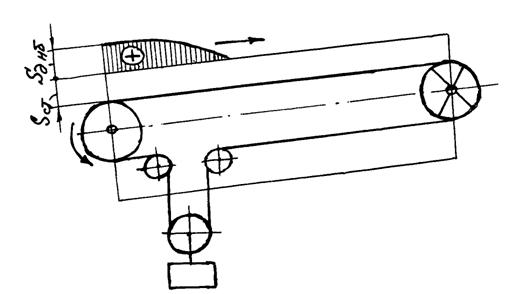
В конвейере с податливым натяжным устройством при приложении к ленте силового импульса от привода вдоль рабочей ее ветви распространяется волна деформаций, которая увеличивает натяжение ленты (рис. 8.1). В рабочей ветви ленты волна деформации уменьшает ее натяжение и гасится ходом натяжного барабана.

80

Рисунок 8.1 – Характер распространения волн деформации в ленте при пуске конвейера с податливым натяжным устройством

В конвейере с жестким натяжным устройством при приложении к ленте силового импульса вдоль рабочей ветви распространяется волна деформации, увеличивающая натяжение, а вдоль нерабочей ветви – волна деформации, уменьшающая натяжение (рис. 8.2). Встречные волны накладываются друг на друга, обходят весь контур, отражаются от привода и от границ ветвей ленты.

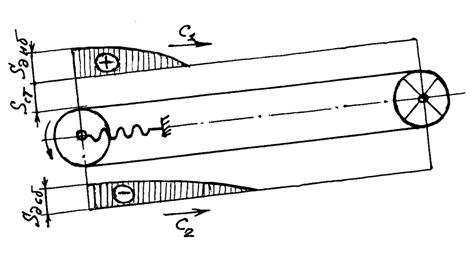
Рисунок 8.2. Характер распространения волн деформации в ленте при пуске конвейера с жёстким натяжным устройством.

8.2. Динамические усилия в ленте конвейера

Для определения динамических усилий в ленте достаточно рассмотреть в пусковой период только прямые волны. Решение уравнения (8.1) для прямой волны представим функцией

U = f(ct + x),

где f – искомая функция.

Динамическое усилие от действия прямой волны в любом сечении х по длине ленты прямо пропорционально скорости перемещения сечения:

Fд.x= C·ρdu/dt.

Для конвейера с податливым натяжным устройством уравнения движения имеет вид:

mпр·dυ/dt + c1ρ1υ = Fд,

где c1 – скорость распространения волны в гружёной ветви ленты; ρ1 – погонная плотность движущихся частей гружёной ветви ленты; υ – линейная скорость обода барабана; c1ρ1υ = Sнб – усилие в ленте в точке набегания; mпр- масса движущихся частей конвейера, приведенная к ободу барабана:

mпр = δ(Jp+Jм)up2·ηп/R2. (8.2)

Здесь Jp и Jм – моменты инерции ротора двигателя и муфты на быстроходном валу; uр – передаточное число редуктора; ηп – КПД привода в пусковой период; R – радиус барабана.

Динамическое окружное усилие, передаваемое ленте от привода в пусковой период,

Fд = (Mп. ср — Мс. п)up/R, (8.3)

где Мп. ср — средний пусковой момент двигателя; Мс. п – статический момент при пуске.

Основная литература [5, с. 144…148]

Дополнительная литература [10, с. 318…321]

Контрольные вопросы:

1.  Напишите уравнение продольных колебаний упругой ленты конвейера.

2.  Какой характер распространения волн деформаций в ленте при пуске конвейеров с податливым и с жёстким (винтовым) натяжным устройством?

3.  Назовите параметры, входящие в уравнение движение конвейера с податливым натяжным устройством.

Лекция 9

Динамика конвейеров с цепным тяговым органом

Работа цепных конвейеров характеризуется пульсирующим движением цепи при постоянной скорости вращения приводной звёздочки. Причина этого заключается в изменении мгновенного радиуса набегания цепи на приводную звёздочку от R до R· (рис.9.1).

Динамические усилия в цепи при пуске

Sд. п = mk·D·ε/(2up), (9.1)

где mk – приводная масса конвейера; D – диаметр звёздочки; up – передаточное число редуктора; ε – угловое ускорение привода:

ε = (Mп. ср — Мс)/Jпр. (9.2)

Здесь Mп. ср – средний пусковой момент двигателя; Мс – статический момент, приведенный к двигателю; Jпр – момент инерции всех движущихся масс, приведенный к двигателю.

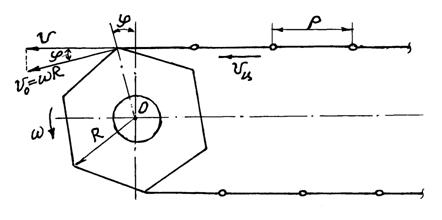
Рисунок 9.1 — Расчётная схема динамики цепного привода

Ускорение цепи при пуске

а = dυ/dt = d(ω R cosφ)/dt = — ω sinφ dφ/dt = -ω2Rsinφ.

Ускорение цепи изменяется по синусоидальной зависимости. При φ = =α/2 его максимальное значение:

amax= ±2π2·υ2/(z02·ρ)= ± 2π2υ2/( z02D), (9.3)

где z0 – число зубьев звёздочки; D – её диаметр.

Наличие этого ускорения вызывает в цепи возникновение динамических деформаций, которые распространяются вдоль неё со скоростью звука υ (м/с) в данной среде, т. е. в упругом стержне, эквивалентном цепи,

υ =,

где Ец – модуль продольной упругости эквивалентного стержня; ρц – плотность упругого, эквивалентного полотну стержня.