Математические основы электродинамики

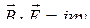, (18.5)

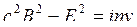. (18.6)

Напряженность магнитного поля и индукция электрического являются компонентами антисимметричного тензора электромагнитного поля

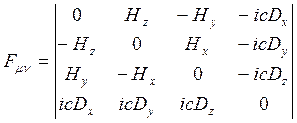, (18.6)

а напряженность электрического и индукция магнитного

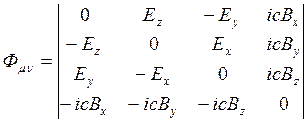. (18.7)

Антисимметричность тензоров проявляется в следующем –

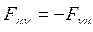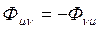, . (18.8)

Антисимметричные тензоры позволяют в компактной форме записать уравнения Максвелла –

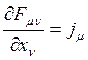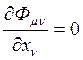, . (18.9)

Записывая фазу электромагнитной волны в компактной четырехмерной форме 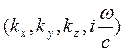и применяя правило преобразования координат четырехмерного вектора, получим выражение, описывающее эффект Доплера –

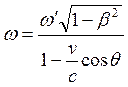, (18.10)

причем при 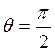имеем поперечный эффект (проявляется только в релятивистском случае).

Вопросы для развернутых ответов

1.  Получите выражения для преобразований электромагнитного поля (на примере электрического или магнитного полей)?

2.  Получите антисимметричный тензор на основе одной из пар уравнений Максвелла?

Литература: [3], глава 16; §75-83.

Основной блок задач

1.  Докажите релятивистскую инвариантность выражений , 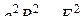с помощью формул преобразований полей и с помощью антисимметричного тензора.

2.  В лабораторной системе отсчета имеется однородное электромагнитное поле, индукция и напряженность которого известны. С какой скоростью должна двигаться система, в которой вектор напряженности электрического поля параллелен индукции магнитного? Единственно ли решение этой задачи?

3.  В лабораторной системе отсчета имеется однородное электромагнитное поле, индукция и напряженность которого известны и перпендикулярны. С какой скоростью должна двигаться система, в которой имеется только электрическое или только магнитное поле?

4.  Найдите величину ЭДС электромагнитной индукции, возникающей при движении проводника в магнитном поле. Воспользуйтесь либо формулами преобразования полей, либо формулами преобразования потенциала.

5.  Используя формулы преобразования четырехмерного вектора, определите изменение частоты электромагнитного излучения при переходе от одной инерциальной системы отсчета к другой.

Дополнительный блок задач

6.  Монохроматическая плоская электромагнитная волна частоты падает под углом на плоское зеркало, которое движется со скоростью в направлении своей нормали, навстречу падающей волне. Определите угол отражения от движущегося зеркала и частоту отраженной волны.

7.  Пользуясь инвариантами электромагнитного поля получите выражение для плотности энергии электромагнитной волны в движущейся системе отсчета, если в покоящейся она равна .

Приложение

Математические основы электродинамики

Теория

Градиентом скалярного поля называют вектор, компоненты которого могут быть найдены с помощью выражения .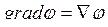

Дивергенция векторного поля – скалярная величина, которая вычисляется как .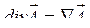

Ротор векторного поля – вектор, компоненты которого рассчитывают в соответствии с формулой .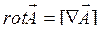

Приведенные выше выражения для расчета градиента, дивергенции и ротора являются инвариантными, то есть их форма записи не зависит от выбора системы координат.

– дифференциальный оператор, форма записи которого зависит от выбранной системы координат.

В прямоугольной декартовой системе координат

;

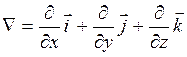в цилиндрической

;

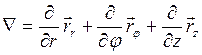в сферической

.

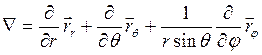В декартовой системе координат градиент, дивергенцию и ротор рассчитывают по следующим формулам:

;

;

.

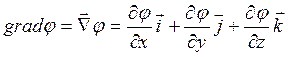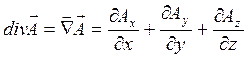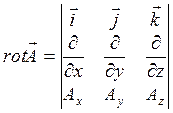Основные тождества

1. 

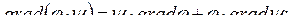
2. 

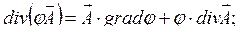
3. 

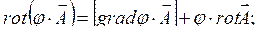
4. 

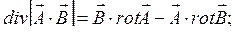
5. 

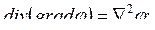
6. 

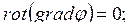
7. 

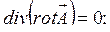
8. 

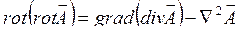
Содержание