Метод эквивалентного генератора
2) Использование законов Кирхгофа
Задаваясь направлениями токов (рис.6) составляем уравнение для одного узла (узел 1) и двух контуров (1321 и 1241) цепи:
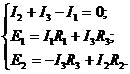 или
или 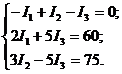
Исключая один из токов 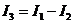 , получаем систему из двух уравнений:
, получаем систему из двух уравнений:
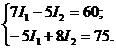
Решением этой системы получаем токи 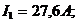
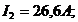
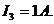
3) Метод контурных токов
Выделим на схеме (рис.6) два независимых контура (1321 и 1241) и составим для них уравнения по второму закону Кирхгофа:
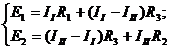 или
или 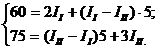
Решая систему уравнений, получим 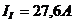 и
и 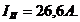
Токи ![]() и
и ![]() направлены одинаково со контурными токами
направлены одинаково со контурными токами ![]()
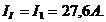 и
и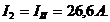
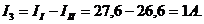
4) Метод узловых напряжений
По ранее приведенной формуле определим межузловое напряжение 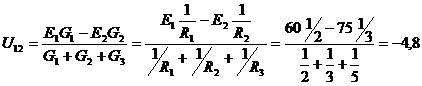 В.
В.
Токи ветвей определяем по второму закону Кирхгофа для контуров где одной из ветвей является межузловое напряжение: 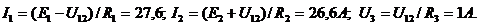
5) Метод эквивалентного генератора
Вначале выделим ветвь 132 в которой надо определить ток, заменив остальную часть цепи по отношению к ней в виде эквивалентного источника с ЭДС 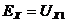 и внутренним сопротивлением
и внутренним сопротивлением 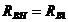 , где
, где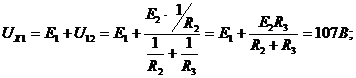
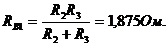
Следовательно, ток ![]() ветви 132 по закону Ома равен
ветви 132 по закону Ома равен
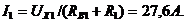
6) Для контроля правильности расчета составим баланс мощностей
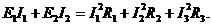
Подставив численные значения токов, сопротивлений и ЭДС, получаем 3651=3651.
7) Потенциальная диаграмма
Рассчитаем и построим потенциальную диаграмму для внешнего контура 13241 приняв потенциал т.2 ![]() Двигаясь от точки 2 с нулевым потенциалом напротив тока
Двигаясь от точки 2 с нулевым потенциалом напротив тока ![]() к точке 3 с большим потенциалом имеем,
к точке 3 с большим потенциалом имеем, 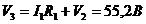 (рис.9). В точке 1 относительно точки 3 потенциал скачком снижается с плюса на минус на величину
(рис.9). В точке 1 относительно точки 3 потенциал скачком снижается с плюса на минус на величину ![]() тогда
тогда 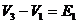 и
и 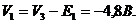 В т.4 потенциал аналогично скачком снижается на
В т.4 потенциал аналогично скачком снижается на ![]()
![]() :
: 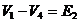 и
и 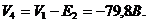 В т.2, откуда течет ток
В т.2, откуда течет ток ![]() к т.4 потенциал выше. Поэтому
к т.4 потенциал выше. Поэтому 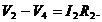 Откуда
Откуда 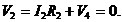
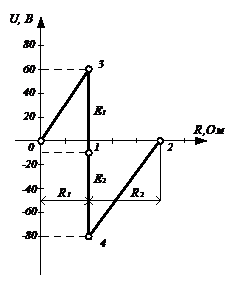
Рис. 9
Практическое занятие № 3
Анализ цепей однофазного синусоидального тока.
Общие сведения
Синусоидальные функции времени могут быть представлены тригонометрической формой записи, диаграммами (графиками) изменения во времени, вращающимися векторами и комплексными числами. Последние две формы записи получил наибольшее применение.
В электротехнике за положительное направление вращения векторов принято направление против хода часовых стрелок. Длина вектора соответствует действующему значению электрической величины, положение относительно оси абсцисс – начальной фазе для момента времени t = 0
Комплексные числа записываются в алгебраической (координатной), тригонометрической и показательной формах соответственно 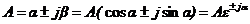 , где
, где ![]() ,
, ![]() — координаты по вещественным
— координаты по вещественным  и мнимой
и мнимой 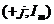 осями;
осями; 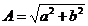 — модуль (длина) вектора;
— модуль (длина) вектора; ![]() — угол относительно вещественной оси +1;
— угол относительно вещественной оси +1; 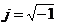 — мнимая единица; e — натуральное число
— мнимая единица; e — натуральное число ![]() .
.


