Метод комплексных чисел

Метод комплексных чисел позволяет графические операции над векторами заменить алгебраическими действиями над комплексными числами с использованием методов расчета цепей постоянного тока.

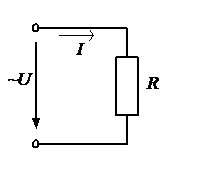
Рис. 10 Рис. 11

В цепи синусоидального тока с активным сопротивлением R (рис. 10) комплексные сопротивление Z=R, комплексное напряжение приняв для удобства совпадающим с вещественной осью ()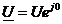, тогда ток . Проводимость , угол сдвига фаз , закон Ома в комплексном виде , через действующие значения . Комплексная мощность равна активной 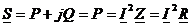. Реактивные мощности и .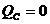

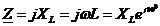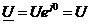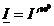В цепи синусоидального тока, содержащей индуктивность L (рис. 12) комплексные сопротивление , напряжение , ток , проводимость , мощность 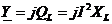; ;. Закон Ома в комплексном виде 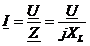, через действующие значения . Угол сдвига фаз между напряжением и током .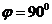

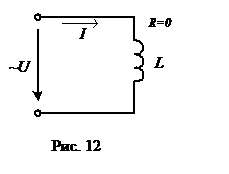
В цепи синусоидального тока, содержащей емкость C (рис. 14) комплексное

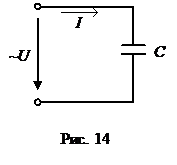
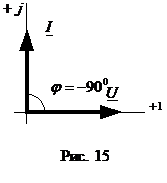
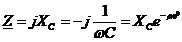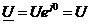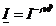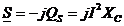сопротивление , напряжение , ток , проводимость , мощность , , . Закон Ома в комплексном виде 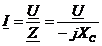, через действующие значения 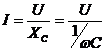. Угол сдвига фаз между напряжением и током .

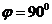Схемы реальных установок составляются набором этих трех элементов. Например, при их последовательном включении 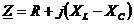, . Сдвиг фазы тока от напряжения определяется соотношением этих сопротивлений .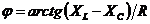

Задача. Для последовательно-параллельной электрической цепи переменного тока (рис.16) определить токи I, I1, I2 на всех участках цепи, активную P, реактивную Q и полную S мощности цепи. Построить векторную диаграмму напряжений и токов. Напряжение питания 127 В, активное и реактивное сопротивления цепи: R =2Ом; R1=15Ом; R2=10Ом; XL=10Ом; XL1=10Ом; XL2=20Ом; XC=2Ом; XC1=20Ом; XC2=30Ом.

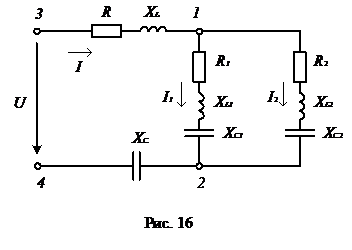
Решение.

1)  Комплексные сопротивления участков цепи в алгебраической и показательной формах записи:

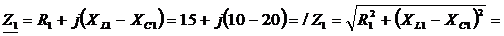
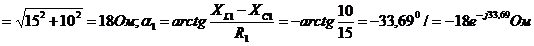
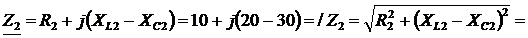
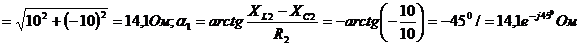
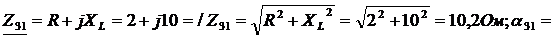
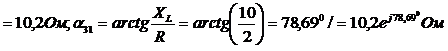
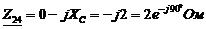
Сопротивление эквивалентное параллельного участка 1-2 найдем методом проводимостей.

2)  Активные проводимости:

первой параллельной ветви: ;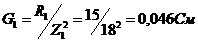

второй параллельной ветви: .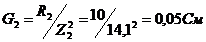

3)  Суммарная активная проводимость параллельного участка цепи: