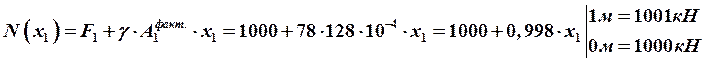Метод определения перемещений мора
– подставляем уравнения изгибающих моментов от внешней и единичной нагрузок в интеграл Мора ( без учета членов, содержащих Q и N ) и вычисляем искомое перемещение.
В данном примере, рассматривается консольная балка (заданная система), следовательно, опоры реакции можно не находить, т. к. отсчет х начнем с точки В (рис. 8, а).
Для нахождения прогиба освободим балку от нагрузки F и приложим
в точке В силу 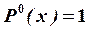 , – 1-я единичная система (рис. 8, б).
, – 1-я единичная система (рис. 8, б).
Для нахождения угла поворота в точке В, приложим момент 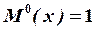 , –
, –
2-я единичная система (рис. 8, в).
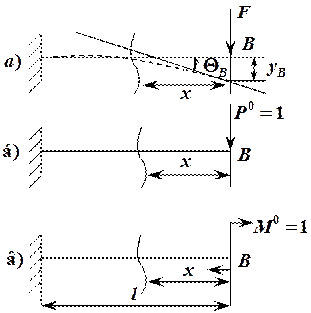
Рис. 8 Метод определения перемещений Мора
Определим значения изгибающих моментов в заданной и единичных системах:
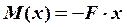 ,
, 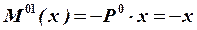 ,
, 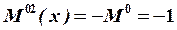 .
.
Для нахождения прогиба подставляем 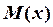 и
и 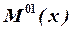 в интеграл Мора:
в интеграл Мора:
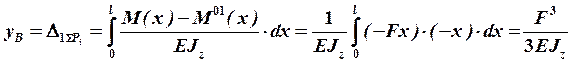 .
.
Для нахождения угла поворота подставляем ![]() и
и 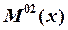 в интеграл Мора:
в интеграл Мора:
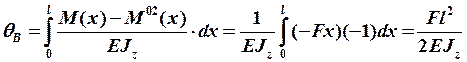 .
.
Перемещения получились положительными, т. к. их направления совпали с направлениями силы 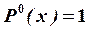 и момента
и момента 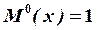 .
.
Метод вычисления перемещений А. К. Верещагина
Сущность правила Верещагина при определении перемещений заключается в том, что интеграл Мора (18) вычисляют графическим способом, путем так называемого “правила перемножения эпюр”:
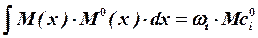 .
.
где ![]() – площадь эпюры
– площадь эпюры 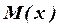 от заданной нагрузки;
от заданной нагрузки;
![]() – ордината эпюры
– ордината эпюры 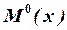 от единичной нагрузки, расположенная под центром тяжести эпюры
от единичной нагрузки, расположенная под центром тяжести эпюры 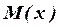 от заданной нагрузки.
от заданной нагрузки.
Подставляя, найдем значение интеграла в формулу (18), получаем формулу для определения перемещений:
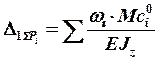 . (19)
. (19)
При применении метода Верещагина умение строить эпюры изгибающих моментов приобретает важнейшее значение, причем надо четко понимать, что он применим только на участках, где одна из эпюр прямолинейна.
Если эпюра 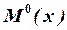 имеет ломаные очертания, то необходимо “перемножать” эпюры порознь для каждого участка, ограниченного прямой линией и результаты складывать.
имеет ломаные очертания, то необходимо “перемножать” эпюры порознь для каждого участка, ограниченного прямой линией и результаты складывать.
Для вычисления перемещений по методу Верещагина требуется знать выражения площадей и координату центра тяжести механических фигур, которые чаще всего встречаются в эпюрах моментов. Эти данные можно найти в приложении.
Порядок вычисление перемещений по методу Верещагина вначале совпадает с порядком, применяемым в методе Мора, но после написания уравнений изгибающих моментов 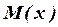 и
и 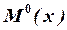 по всем силовым участкам системы необходимо построить эпюры этих моментов. Затем эпюру
по всем силовым участкам системы необходимо построить эпюры этих моментов. Затем эпюру 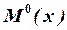 разбивают на участки, ограниченные прямой линией, подсчитывают площади эпюры
разбивают на участки, ограниченные прямой линией, подсчитывают площади эпюры 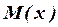 в границах этих участков и определяют положение их центров тяжести.
в границах этих участков и определяют положение их центров тяжести.
Далее, как правило, из подобия треугольников, определяют значения ![]() против соответствующих центров тяжести и, перемножая по участкам
против соответствующих центров тяжести и, перемножая по участкам ![]() и
и ![]() , складывают полученные результаты. После деления на жесткость
, складывают полученные результаты. После деления на жесткость ![]() находим значения искомых перемещений.
находим значения искомых перемещений.
Рассмотрим пример применения метода Верещагина на уже знакомой нам консольной балке (рис. 9).
Определим значения изгибающих моментов в заданной и единичных системах:
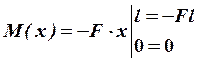 ,
, 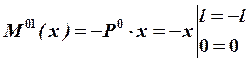 ,
, 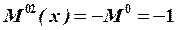 .
.
Вычислим площадь эпюры 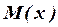 в заданной системе:
в заданной системе:
 .
.
Определим значения ординат ![]() в единичных системах:
в единичных системах:
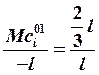 →
→ 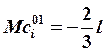 ;
; 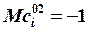 .
.
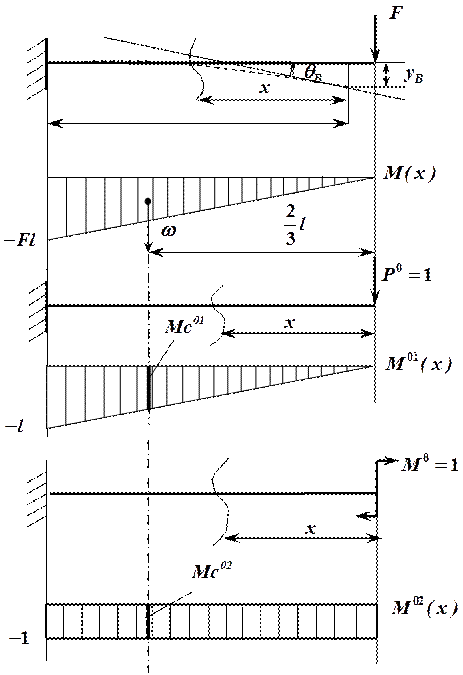
Рис. 9 Метод определения перемещений Верещагина
По формуле (19) определяем значения прогиба и угла поворота:
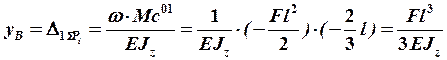 ,
,
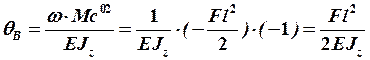 .
.
Перемещения получились те же, что и в ранее разобранном случае.
7 Статически неопределимая система
Система является статически неопределимой, если внутренние силовые факторы в поперечных сечениях, составляющих ее стержень, не могут быть определены только из уравнений статики. Причиной статической неопределимости является наличие в системе лишних связей, то есть таких связей, которые необязательны для обеспечения геометрической неизменяемости системы. Лишними связями могут служить дополнительные опоры, например, шарнирно-подвижные опоры (рис. 10).
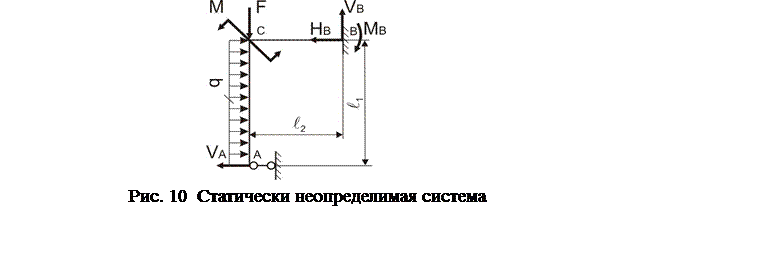
Системы, подобные изображенной, называют внешне статически неопределимыми в том смысле, что уравнений статики недостаточно для определения опорных реакций «лишних» связей, являющихся внешними силами.
Общее количество «лишних» связей (как внешних, так и внутренних) называется степенью статической неопределимости системы. Так, заданная система один раз статически неопределима.
Расчет статической неопределимости системы начинают с выяснения степени ее статической неопределимости. Для сравнительно простых рам, рассматриваемых в курсе сопротивления материалов, степень статической неопределимости в подавляющем большинстве случаев можно установить, подсчитав, сколько связей нужно отбросить, для того, чтобы заданная статически неопределимая система превратилась в статически определимую.
Для раскрытия статической неопределимости систему освобождают от «лишних» связей, превращая тем самым заданную статически неопределимую систему в геометрически неизменяемую статически определимую систему, называемую основной системой (рис. 11).
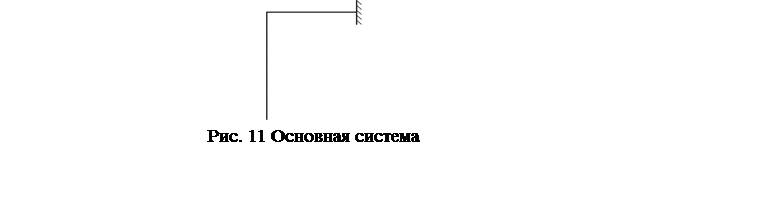
Основная система, к которой приложены заданные внешние силы и реакции отброшенных связей, эквивалентна заданной системе, то есть в ней возникают такие же внутренние силовые факторы и такие же перемещения, как и в заданной системе. Указанное обстоятельство используется для определения лишних неизвестных. Действительно, в заданной системе не может быть перемещений в направлениях имеющихся в ней связей, следовательно, и в основной системе перемещения в направлениях отброшенных связей, вызванные действием заданных сил и искомых лишних неизвестных, должны быть равны нулю. Иными словами, реакции отброшенных связей должны иметь такие значения, при которых перемещения по их направлениям равнялись бы нулю.
Математическими выражениями сформулированного положения являются уравнения перемещений. Так, для один раз статически неопределимой рамы можно выбрать в качестве основной системы раму с отброшенной шарнирно-подвижной опорой и принять за лишнюю неизвестную реактивную силу ![]() указанной опоры. Основная система, нагруженная заданными силами и лишней неизвестной, представлена на рис. 12. Перемещение
указанной опоры. Основная система, нагруженная заданными силами и лишней неизвестной, представлена на рис. 12. Перемещение ![]() по направлению
по направлению ![]() равно нулю.
равно нулю.
Применяя принцип независимости действия сил, можем записать уравнение перемещений в виде:
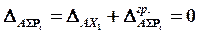 , (20)
, (20)
где ![]() – перемещение по направлению отброшенной связи в опоре
– перемещение по направлению отброшенной связи в опоре ![]() от действия силы
от действия силы ![]() ;
;
![]() – перемещение в том же направлении от действия заданной нагрузки.
– перемещение в том же направлении от действия заданной нагрузки.

В данной работе определение перемещений производится методом Мора и с использованием метода Верещагина, поэтому оказывается удобным выразить перемещение ![]() через перемещение
через перемещение ![]() от единичных сил, умножая его на лишнюю неизвестную
от единичных сил, умножая его на лишнюю неизвестную ![]() . Таким образом, для рассматриваемой линейно-деформируемой системы будем иметь:
. Таким образом, для рассматриваемой линейно-деформируемой системы будем иметь:
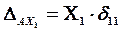 .
.
Так как ![]() – перемещение по направлению силы
– перемещение по направлению силы 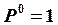 от действия всей внешней нагрузки, переходим к другой форме записи уравнения (20):
от действия всей внешней нагрузки, переходим к другой форме записи уравнения (20):
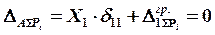 . (21)
. (21)
Первый индекс у каждого из перемещений указывает номер единичной силы или момента, в направлении которого происходит данное перемещение; второй индекс указывает причину, вызывающую перемещение по тому же направлению.
Уравнения перемещений носят название канонических уравнений метода сил. Каноническими эти уравнения называются потому, что составляются они всегда по одному и тому же правилу (канону) и их вид зависит от степени статической неопределимости системы и не зависит от ее конкретных особенностей. Указание, что уравнения относятся к методу сил, подчеркивает, что искомыми неизвестными, определяемыми из этих уравнений, являются силы или моменты от действия сил. Уравнение записано для системы с одним лишним неизвестным; аналогично могут быть составлены системы канонических уравнений при любом другом числе лишних неизвестных:
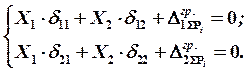 (22)
(22)
Наиболее надежной проверкой правильности определения лишних неизвестных и построения эпюр внутренних силовых факторов для заданной системы является ее повторное решение при другом выборе основной системы. Совпадение окончательных эпюр, полученных в результате двух указанных решений, является гарантией их правильности.
Большая трудоемкость такой проверки заставляет в большинстве случаев от нее отказаться, ограничиваясь так называемыми статической и деформационной проверками.
Первая из них заключается в проверке равновесия некоторой отсеченной части рамы под действием приложенных к ней внешних сил и внутренних силовых факторов, заменяющих действие отброшенных частей рамы на оставленную.
При деформационной проверке производится перемножение окончательной эпюры изгибающих моментов, построенной для заданной системы, на единичную эпюру. Результат указанного перемножения должен быть равен нулю.
ТЕМЫ И ВАРИАНТЫ ЗАДАНИЙ
Расчетно-графическая работа № 1 «Расчет элементов конструкций»
Задание 1 Осевое растяжение (сжатие) стержня
Расчетные схемы изображены на рис. 13, исходные данные выбираются из табл. 1.
Для ступенчатого стального стержня (модуль упругости 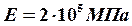 , удельный вес
, удельный вес 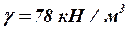 ) требуется:
) требуется:
1. Построить эпюру продольных сил.
2. Подобрать размеры поперечного сечения стержня при допускаемом напряжении ![]() ;
;
3. Составить аналитические выражения, с учетом действия собственного веса и построить эпюры продольных сил и нормальных напряжений.
3. Вычислить величину продольной деформации каждого участка.
4. Определить полную абсолютную деформацию стержня.
Рис. 13 Расчетные схемы к заданию № 1
Таблица 1 Исходные данные к заданию № 1
|
№№ |
А1/А |
F1 |
F2 |
F3 |
а |
в |
c |
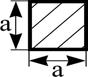
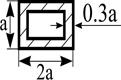
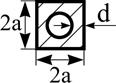
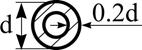
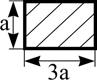
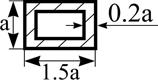
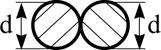
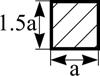
Поперечное сечение |
|
кН |
м |
|||||||
|
11 |
0,9 |
1100 |
1200 |
2000 |
1,0 |
0,9 |
0,6 |
|
|
22 |
0,8 |
1200 |
1300 |
1900 |
1,2 |
0,8 |
0,7 |
|
|
33 |
0,7 |
1300 |
1000 |
1800 |
1,3 |
0,7 |
0,8 |
|
|
44 |
0,6 |
1400 |
800 |
1700 |
1,4 |
0,6 |
0,9 |
|
|
55 |
0,5 |
1500 |
900 |
1600 |
1,5 |
0,5 |
1,5 |
|
|
66 |
0,6 |
1600 |
700 |
1500 |
0,9 |
1,0 |
1,4 |
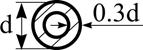
d |
|
77 |
0,7 |
1700 |
600 |
1400 |
0,8 |
1,2 |
1,3 |
|
|
8 |
0,8 |
1800 |
500 |
1300 |
0,7 |
1,3 |
1,2 |
|
|
99 |
0,9 |
1900 |
1100 |
1200 |
0,6 |
1,4 |
1,0 |
|
|
00 |
0,5 |
2000 |
400 |
1100 |
0,5 |
1,5 |
1,0 |
|
|
д |
е |
д |
е |
д |
е |
д |
е |
|
Задание 2 Кручение стержня круглого поперечного сечения
Расчетная схема изображена на рис. 14, исходные данные выбираются из табл. 2.
Стальной вал равномерно вращается, передавая крутящие моменты ![]() ,
, ![]() и
и ![]() через ведомые шкивы на различные механизмы.
через ведомые шкивы на различные механизмы.
Требуется:
1. Определить крутящий момент ![]() на ведущем шкиве.
на ведущем шкиве.
2. Построить эпюру крутящих моментов.
3. Определить рациональное расположение шкивов на валу.
4. Подобрать диаметр вала в опасном сечении.
5. Проверить прочность вала при кручении.
6. Определить деформации в характерных сечениях вала и построить эпюру углов закручивания (G = 8∙104 МПа).
7. Проверить вал на жесткость по максимальным деформациям.
Таблица 2 Исходные данные к заданию № 2
|
№ |
a |
b |
c |
M2 |
M3 |
M4 |
|
|
м |
Н×м |
МПа |
|||||
|
1 |
0,20 |
0,31 |
0,10 |
200 |
110 |
200 |
30 |
|
2 |
0,21 |
0,32 |
0,11 |
190 |
120 |
190 |
35 |
|
3 |
0,22 |
0,33 |
0,12 |
180 |
130 |
180 |
40 |
|
4 |
0,23 |
0,34 |
0,13 |
170 |
140 |
170 |
45 |
|
5 |
0,24 |
0,35 |
0,14 |
160 |
150 |
160 |
50 |
|
6 |
0,25 |
0,36 |
0,15 |
150 |
160 |
150 |
55 |
|
7 |
0,26 |
0,37 |
0,16 |
140 |
170 |
140 |
60 |
|
8 |
0,27 |
0,38 |
0,17 |
130 |
180 |
130 |
65 |
|
9 |
0,28 |
0,39 |
0,18 |
120 |
190 |
120 |
70 |
|
0 |
0,29 |
0,30 |
0,90 |
110 |
200 |
110 |
75 |
|
д |
е |
д |
е |
д |
е |
д |
Рис. 14 Расчетные схемы к заданию № 2
Задание 3 Расчет на прочность при изгибе
Расчетная схема изображена на рис. 15, исходные данные выбираются из табл. 3.
Для заданной схемы балки требуется:
1. Определить значения опорных реакций
2. Построить эпюры поперечных сил ![]() и изгибающих моментов
и изгибающих моментов ![]() .
.
3. По допускаемым напряжениям ![]() подобрать размеры заданных профилей поперечного сечения.
подобрать размеры заданных профилей поперечного сечения.
4. По выбранным размерам поперечного сечения вычислить нормальные напряжения и сравнить их с допускаемыми напряжениями, при этом перегрузка не должна превышать 5 %.
![]()
Рис. 15 Расчетные схемы к заданию № 3
Таблица 3 Исходные данные к заданию № 3
|
№ |
М |
F1 |
F2 |
q1 |
q 2 |
a |
b |
c |
Поперечное сечение |
|
|
кH∙м |
кH |
кH/м |
м |
|||||||
|
1 |
18 |
30 |
8 |
22 |
8 |
2,6 |
1,0 |
3,0 |
|
|
|
2 |
20 |
28 |
10 |
20 |
10 |
2,4 |
1,2 |
2,8 |
|
|
|
3 |
22 |
26 |
12 |
18 |
12 |
2,2 |
1,4 |
2,6 |
|
|
|
4 |
20 |
24 |
14 |
16 |
14 |
2,0 |
1,6 |
2,4 |
|
|
|
5 |
26 |
22 |
16 |
14 |
16 |
1,8 |
1,8 |
2,2 |
|
|
|
6 |
28 |
20 |
18 |
12 |
18 |
1,6 |
2,0 |
2,0 |
|
|
|
7 |
30 |
18 |
20 |
10 |
20 |
1,4 |
2,2 |
1,8 |
|
|
|
8 |
32 |
16 |
22 |
8 |
22 |
1,2 |
2,4 |
1,6 |
|
|
|
9 |
34 |
14 |
24 |
6 |
24 |
1,0 |
2,6 |
1,4 |
|
|
|
0 |
36 |
12 |
26 |
4 |
26 |
3,0 |
2,8 |
1,2 |
|
|
|
д |
е |
д |
е |
д |
е |
д |
е |
д |
е |
|
Расчетно-графическая работа № 2
Расчет статически неопределимой системы
Задание состоит из одной задачи, расчетная схема изображена на рис. 16, исходные данные выбираются из табл. 4.
Задано: стальная конструкция (рама), допускаемые напряжения – 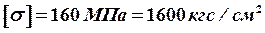 ,
, 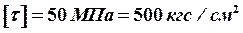 .
.
Требуется:
1. Вычертить заданную схему элемента с приложенными нагрузками, соблюдая масштаб длин, проставить значения размеров и нагрузок.
2. Раскрыть степень статической неопределимости элемента.
3. Выбрать основную и эквивалентную системы. Используя принцип независимости действия сил, разложить эквивалентную систему на грузовую и систему, нагруженную неизвестной реакцией ![]() .
.
4. Построить единичную систему и изобразить на расчетных схемах деформацию осей всех систем и перемещения ![]() ,
, ![]() и
и ![]() написать условие совместности деформаций
написать условие совместности деформаций ![]() .
.
5. Написать каноническое уравнение метода сил – уравнение совместности деформаций 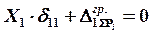 .
.
6. Определить значения изгибающих моментов грузовой и единичной систем и построить эпюры.
7. Определить неизвестные коэффициенты канонического уравнения ![]() и
и ![]() методами Мора и Верещагина, найти неизвестную реакцию
методами Мора и Верещагина, найти неизвестную реакцию ![]() .
.
8. Вычислить значения внутренних усилий на каждом силовом участке и построить окончательные эпюры.
9. Сделать статическую проверку.
10. Сделать проверку равенства нулю перемещения по направлению отброшенной связи 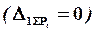 , подтверждающую правильность определения реакции
, подтверждающую правильность определения реакции 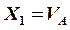 , используя методы Мора и Верещагина.
, используя методы Мора и Верещагина.
11. Подобрать поперечные сечения конструкции, состоящей из двутавровой балки и проверить конструкцию на прочность по касательным напряжениям.
Таблица 4 Исходные данные к расчетно-графической работе № 2
|
№ |
Длина участков, |
Заданная нагрузка |
||||
|
|
|
|
|
|
|
|
|
1 |
1,0 |
2,0 |
2,8 |
10 |
20 |
10 |
|
2 |
1,2 |
2,2 |
2,6 |
12 |
22 |
12 |
|
3 |
1,4 |
2,4 |
2,4 |
14 |
24 |
14 |
|
4 |
1,6 |
2,6 |
2,2 |
16 |
26 |
16 |
|
5 |
1,8 |
2,8 |
2,0 |
18 |
28 |
18 |
|
6 |
2,0 |
1,0 |
1,8 |
20 |
10 |
20 |
|
7 |
2,2 |
1,2 |
1,6 |
22 |
12 |
22 |
|
8 |
2,4 |
1,4 |
1,4 |
24 |
14 |
24 |
|
9 |
2,6 |
1,6 |
1,2 |
26 |
16 |
26 |
|
0 |
2,8 |
1,8 |
1,0 |
28 |
18 |
28 |
|
д |
е |
д |
е |
д |
е |
|
![]()
Рис. 16 Расчетные схемы к расчетно-графической работе № 2
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Расчетно-графическая работа № 1 «Расчет элементов конструкций»
Задание 1 Осевое растяжение (сжатие) стержня
Ступенчатый стальной стержень (рис. 17) находится под действием продольных сил и сил тяжести.
Задано: 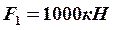 ,
, 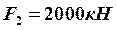 ,
,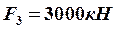 ,
, 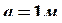 ,
,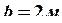 ,
, 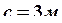 .
.
Расчёт начинаем с определения количества участков, подлежащих рассмотрению. Так как продольные силы ![]() и напряжения
и напряжения ![]() зависят от внешних сил, площади поперечного сечения и удельного веса материала, то границами участков будут точки приложения внешних сил и места изменения сечения.
зависят от внешних сил, площади поперечного сечения и удельного веса материала, то границами участков будут точки приложения внешних сил и места изменения сечения.
Исходя из этого, для рассматриваемого ступенчатого стержня следует принять 3 силовых участка.
![]()
Рис. 17 Расчетная схема, эпюры ![]() и
и ![]()
1. Определяем для каждого участка величину продольной силы, применяя метод сквозного разреза (сечений). Для этого в произвольном месте на силовом участке проведём сечение перпендикулярно оси стержня и рассмотрим условие равновесия нижней части. Действие отброшенной части на оставшуюся заменяем внутренней продольной силой 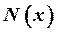 .
.
Составим уравнение равновесия для первого участка:
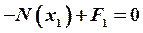 ;
;
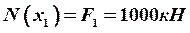 .
.
Проведя сечения на следующих участках и рассматривая равновесие частей стержня, получим:
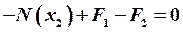 ;
;
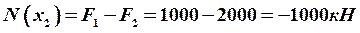 .
.
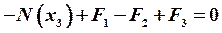 ;
;
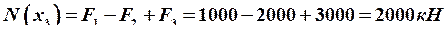 .
.
Строим эпюру продольных сил.
2. Подбор размеров допускаемого поперечного сечения производим по критерию прочности:
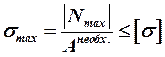 .
.
Производим расчет площади поперечного сечения того участка, где действует наибольшая продольная сила, в данном примере участок с площадью ![]() :
:
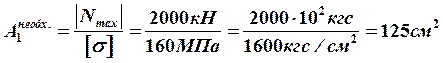 ;
;
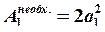 .
.
Основание 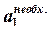 равно:
равно:
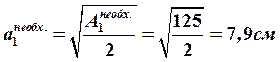 .
.
Принимаем 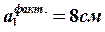 . Тогда
. Тогда 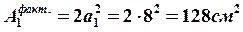 .
.
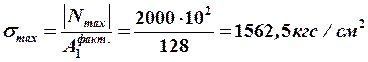 .
.
Определяем перегрузку (недогрузку):
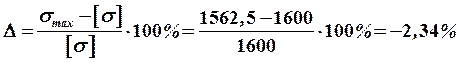 .
.
Перегрузка (недогрузка) не должна превышать ![]() .
.
Из соотношения 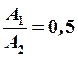 определяем площадь поперечного сечения:
определяем площадь поперечного сечения:
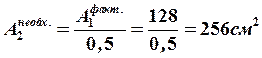 .
.
Тогда 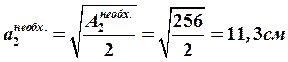 .
.
Принимаем 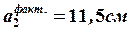 . Тогда
. Тогда 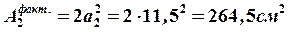 .
.
3. Составляем аналитические выражения продольных сил и нормальных напряжений с учетом действия собственного веса для всех силовых участков.
Для удобства расчета площадь поперечного сечения переводим в ![]() :
: 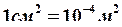 , расчет напряжений проводим в
, расчет напряжений проводим в ![]() :
: 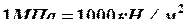 .
.
![]()