Метод последовательных приближений
2.2. Метод последовательных приближений
Неизохронность колебаний математического маятника связана с нелинейностью описывающего их уравнения (2.7). Общих методов решения нелинейных ДУ не существует, но есть несколько приближенных методов. Дальше мы рассмотрим один из таких методов — метод последовательных приближений.
Сначала проделаем на примере маятника, а потом приведём к общему виду. Разложим нелинейное слагаемое sin(x) в уравнении (2.7) в ряд Тейлора, ограничиваясь вторым слагаемым
|
|
(2.10) |
здесь a = -1/6.
Зависимость периода колебаний от амплитуды (неизохронность колебаний) определяется коэффициентом a. Если a = 0 колебания чисто изохронные и период T = 2p/w0.
Дальше воспользуемся теоремой из теории ДУ, что решение ДУ непрерывно зависит от параметра. Так как есть период, зависящий от w0 то можно сказать, что w0 — это параметр системы, который совпадает с частотой линейных колебаний. Введём параметр w — частота действующих (свободных) колебаний w = 2p/T(a). Мы знаем, что при a = 0, она совпадает с w0, и непрерывно зависит от a, т. е. мы можем представить её в виде ряда по степеням a. Исторически сложилось (да и проще) раскладывать w2:
|
|
(2.11) |
Считая нелинейность малой, мы ограничиваемся только первым слагаемым, содержащим a. Подставим (2.11) в (2.10), тогда, сохраняя только первые степени по a, получим
|
|
(2.12) |
Решение x(t) уравнения (2.12) тоже непрерывно зависит от параметра a, причём при a = 0
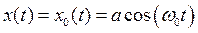 .
.
В силу непрерывности решения по a, можно записать, ограничиваясь только первой степенью a, что при a ¹ 0,
![]() .
.
Подставим это решение в (2.12), пренебрегая степенями a со второй включительно
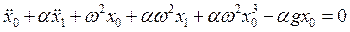 ,
,
и, учитывая уравнение нулевого приближения для x0
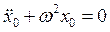 ,
,
получим окончательное уравнение первого приближения
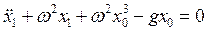 .
.
В нашем случае, выбирая начальные условия в виде t = 0, x = a, ![]() , находим решение уравнения нулевого приближения
, находим решение уравнения нулевого приближения
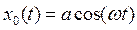 .
.
Уравнение первого приближения соответственно будет
|
|
(2.13) |
У нас получилось линейное уравнение, в правой части которого стоят гармонические силы. Получилось, что на систему с собственной частотой w действуют два гармонических процесса с частотами w и 3w. Так как потерь нет, то колебания совершаются с бесконечной амплитудой (на частоте w резонанс), поэтому, чтобы такого не было, необходимо положить
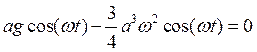 ,
,
тогда уравнение первого приближения примет вид:
|
|
(2.14) |
Из предыдущего соотношения находим, что 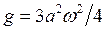 . Тогда, подставив его в (2.11), получим
. Тогда, подставив его в (2.11), получим
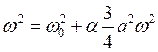 ,
,
следовательно
|
|
(2.15) |
Решение уравнения первого приближения будет иметь вид:
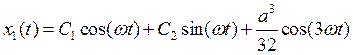 ,
,
где С1 и С2 — произвольные постоянные. Тогда полное решение (2.10) в первом приближении запишется следующим образом:
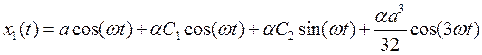 .
.
Значения произвольных постоянных можно найти, требуя от этого решения, чтобы оно удовлетворяло тем же начальным условиям, т. е. 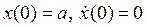 , тогда окончательно с учётом формулы (2.15)
, тогда окончательно с учётом формулы (2.15)
|
|
(2.16) |
Из найденного соотношения видно, что колебания не изохронные и в них присутствуют высшие гармоники. Для математического маятника частота свободных колебаний убывает с ростом их амплитуды.
2.3. Свободные колебания в резонансном контуре с нелинейной ёмкостью без затухания Вопрос 5
|
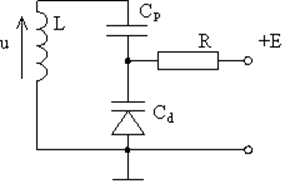
Рассмотрим параллельный резонансный контур, представленный на рис. 19. Здесь в качестве нелинейной ёмкости используется варикап, причём ёмкость разделительного конденсатора Сp много больше ёмкости варикапа Cd. Известен закон изменения ёмкости p-n перехода: |
Рис. 19. Колебательный контур с нелинейной ёмкостью. |
|
|
(2.17) |
|
Проинтегрируем (2.17), тогда получим:
|
|
Из последнего уравнения найдём uak:
|
|
(2.18) |
В качестве обобщённых координат возьмём напряжение на индуктивности, т. е. u = E + uak. Если u = 0, значит к варикапу приложено управляющее напряжение. В этом случае мы можем выразить константы через известные величины. Получается, что q = 0, Cd = C0, тогда
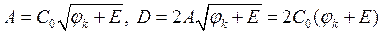 .
.
Подставим эти выражения в (2.18)
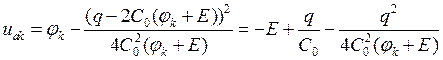 ,
,
тогда для обобщённой координаты получаем
|
|
(2.19) |
Заметим, что полярность управляющего напряжения E выбрана так, чтобы варикап находился в состоянии обратного смещения, чтобы конденсатор Cр не влиял на работу. Выберем Cp >> Cd, тогда при колебаниях напряжение на Cp не будет сильно меняться и тогда можно считать, что напряжение, приложенное к катушке будет u. В таком случае для контура можно записать второй закон Кирхгофа в виде
|
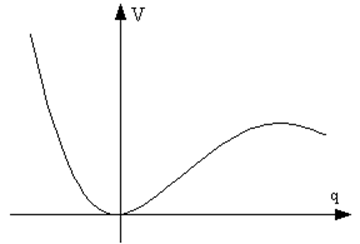
Рис. 20. График потенциальной энергии. |
|
(2.20) |
|
Уравнение колебаний имеет вид (2.1), что позволяет с учётом (2.19) ввести потенциальную энергию в виде |
||
|
|
(2.21) |
|
|
Примерный вид полученной зависимости показан на рис. 20. Перепишем уравнение (2.20) в следующем виде
|
Тогда уравнение для фазовой траектории будет выглядеть так:
|
|
(2.22) |
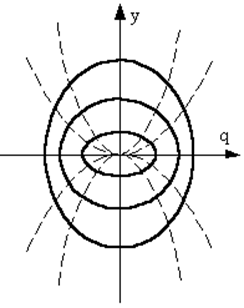
Построим фазовый портрет для этой системы методом изоклин. Найдём для этого семейства фазовых траекторий изоклины, т. е. линии с постоянным наклоном. Уравнение изоклин:
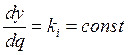 ,
,
отсюда, с учётом (2.22), для нашей системы получается
|
Рис. 21. Построение фазовых траекторий методом изоклин. |
Изоклины, исходя из полученного уравнения, по сути, параболы. Коэффициент ki определяет крутизну. Он может быть как отрицательным, так и положительным, соответственно изоклины будут находиться выше оси или ниже оси абсцисс. Если ki = 0, парабола выльется в вертикальную линию q = 0, а если ki = ¥, то в горизонтальную y = 0. На рис. 21 показано построение фазовых траекторий методом изоклин. Замкнутость фазовых траекторий подтверждает, что мы имеем дело с консервативной системой. Из фазового портрета видно, что при малых амплитудах колебаний, как и в случае идеального маятника, фазовые траектории близки к эллипсам, т. е. малые движения в нелинейной системе близки к гармоническим колебаниям в нелинейной системе. Это связано с тем, что при малых значениях q влиянием нелинейного члена g0q2 |
по сравнению с линейным членом q на колебательный процесс системе можно пренебречь.
Проделаем то же самое не графически, а аналитически. Воспользуемся методом последовательных приближений. Для этого опять перепишем уравнение (2.20), но уже в форме уравнения (2.10):
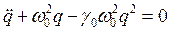 .
.
Опять действуем точно также: установившуюся частоту разложим в ряд
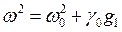 .
.
Также можно записать, ограничиваясь только первой степенью g0,
![]() .
.
Уравнение нулевого приближения в данном случае имеет вид
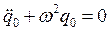 ;
;
его решение при начальных условиях 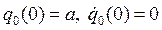 будет таким:
будет таким:
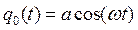 .
.
Первое приближение имеет вид:
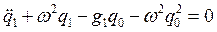 .
.
Подставляя решение для q0, получаем
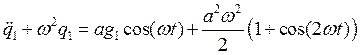 .
.
Заметим, на систему с резонансной частотой w воздействует внешняя сила с той же самой частотой, т. е. для секулярных решений получается следующее условие: g1 = 0. Таким образом, мы приходим к выводу, что поправка первого порядка отсутствует, поэтому будем раскладывать до следующего параметра, т. е. для частоты, с учётом равенства нулю g1, получаем
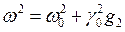 .
.
Соответственно
![]() .
.
Тогда уравнение второго приближения, примет вид
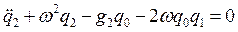 .
.
Или, подставив решения для q0 и q1, получим
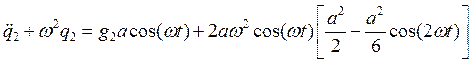 .
.
Чтобы исчезли секулярные слагаемые, нужно потребовать, чтобы 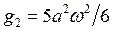 , тогда мы можем найти зависимость частоты от амплитуды:
, тогда мы можем найти зависимость частоты от амплитуды:
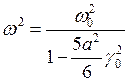 .
.
Итак, мы рассмотрели систему с одной степенью свободы без диссипации. Перейдём теперь к следующему уровню.
Тема 3. Свободные колебания в диссипативных системах с одной степенью свободы Вопрос 6
В неконсервативных системах полная энергия не сохраняется, поэтому уравнение фазовых траекторий уже не может иметь вид уравнения (2.5). Мы можем записать его с учётом соотношения (1.35), где введена функция Рэлея, которая описывает убыль энергии. Функция Рэлея:
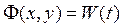 ;
; ![]()
Так как функция F(x, y) описывает убыль энергии, то можно сказать, что функция W(t) определяет запас колебательной энергии системы. В консервативной системе она бы сохранялась. Естественно, что для автономных диссипативных систем dW/dt < 0, т. е. энергия с течением времени уменьшается.
Для простейшей диссипативной системы уравнение (2.5) принимает вид:
|
Рефераты по физике сдают здесь
Другие статьиПохожая информацияУзнать стоимость за 15 минут
Распродажа дипломных
Подпишись на наш паблик в ВК
Нужна работа?
|
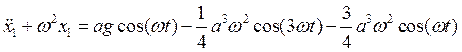 .
.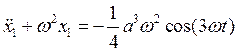 .
.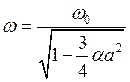 .
.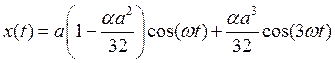 .
.
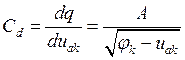 .
.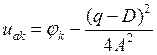 .
.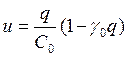 , где
, где 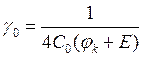 .
.
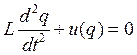 .
.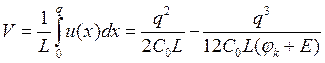 .
.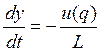 ;
; 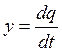 .
.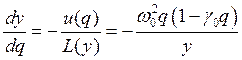 , где
, где 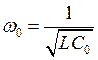 .
.
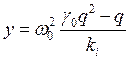 .
.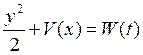 ;
; 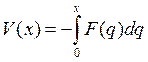 .
.

