Определение диэлектрической проницаемости вещества

Упражнение II

Определение диэлектрической проницаемости вещества

1. Измерить толщину d стеклянной пластины. Поместить её между обкладками измерительного конденсатора.

2. Используя схему, представленную на рис. 2, измерить 3 раза напряжения U и U0 , внося результаты в таблицу 3.

3. Повторить пп. 1 и 2 для других диэлектриков: оргстекла, текстолита и картона.

4. Рассчитать средние значения и для каждого диэлектрика, затем, используя формулу

,

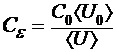найти значение . электроёмкости измерительного конденсатора с диэлектриком.

5. Используя среднее значение воздушного конденсатора из упражнения I и значения из упражнения II, определить с помощью формулы (4) диэлектрическую проницаемость всех испытанных диэлектриков.

Таблица 3

Контрольные вопросы

1.  Цели работы.

2.  Какие вещества называются диэлектриками?

3.  Полярные и неполярные диэлектрики.

4.  Механизмы поляризации полярных и неполярных диэлектриков

Электрический дипольный момент.

5. Поляризованность. Диэлектрические восприимчивость и прони — цаемость.

6. Поле однородно заряженной плоскости.

7. Поле воздушного плоского конденсатора.

8. Поле плоского конденсатора, заполненного диэлектриком.

9. Емкость плоского конденсатора (воздушного и заполненного диэлектриком). Принцип измерения диэлектрической проницаемости с помощью этих величин.

10. Содержание лабораторных упражнений, порядок их выполнения.

Литература

1. А. В. Астахов, Ю. М. Широков. Курс физики. М.: «Наука», 1980. Т. II. 359 с.

2. Р. Фейнман, Р. Лейтон, М. Сэндс. Фейнмановские лекции по физике. М.: «Мир», 1966. Вып. 5. 296 с.

3.  Д. В. Сивухин. Общий курс физики. Т. III. Электричество. М.: «Наука», 1977. 688 с.

4. И. Е. Иродов. Электромагнетизм. Основные законы. М.-СПб.: Физматлит, 2000. 350 с.

Лабораторная работа Э.3

ИЗМЕРЕНИЕ

ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ

ГЕОМАГНИТНОГО ПОЛЯ

Цель работы

Проведение измерений горизонтальной составляющей магнитного поля Земли, основывающееся на использовании закона Био-Савара.

Теоретическое введение

Магнитное поле оказывает силовое воздействие только на движущийся в нем заряд (а значит, и на электрический ток). В случае точечного заряда эта сила равна

F = q [v B] . (1)

Здесь q – величина заряда, v – его скорость в точке r в момент времени t, вектор B – индукция магнитного поля (часто называемая просто магнитным полем) в той же точке и в тот же момент времени, квадратными скобками обозначено векторное произведение заключенных в них сомножителей. Напомним, что векторное произведение [] двух векторов a и b — это вектор, перпендикулярный к a и b и равный по абсолютной величине 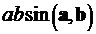. Направление вектора [] соответствует требованию, чтобы векторы a, b и [] образовывали правовинтовую систему. Сила F, выражаемая формулой (1), называется магнитной силой Лоренца.

В данной работе изучаются стационарные (не зависящие от времени) магнитные поля. В лабораторных условиях такие поля создаются постоянными токами. Как видно из названия работы, речь пойдет и о геомагнитном поле, которое во временн’ых рамках проведения измерений также

стационарно. Линия, касательная к которой в любой ее точке совпадает по направлению с вектором магнитной индукции в той же точке, называется силовой линией магнитного поля. Силовые линии магнитного по­ля всегда замкнуты.

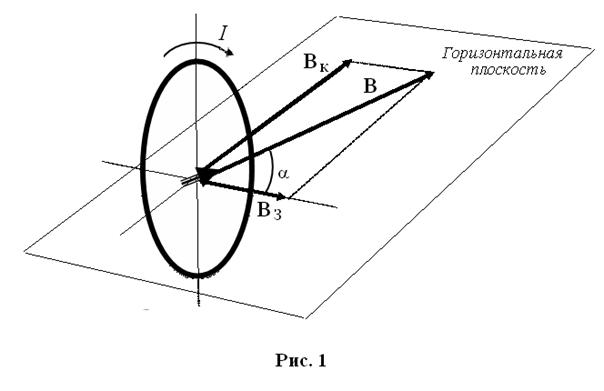
Физическая идея, лежащая в основе измерений данной работы, состоит в следующем. Представим себе, что по круговому (радиуса R) витку провода, расположенному в вертикальной плоскости протекает стационарный ток I. На рис. 1 этот виток изображен толстой овальной линией, левая часть которой считается более удаленной от читателя по сравнению с правой. Вертикальная линия, проходящая через центр витка, является осью вращения магнитной стрелки. Сама магнитная стрелка (на рисунке представлена коротким толстым вектором) лежит, естественно, в горизонтальной плоскости. Центр стрелки совмещен с центром витка.

Вектор Вк — это магнитное поле в центре кольцевого1 тока I. Этот вектор перпендикулярен плоскости витка и ориентирован так, как показано на рисунке. Абсолютная величина и направление вектора Вк даются законом Био-Савара. Вектор ВЗ — это горизонтальная составляющая вектора магнитного поля Земли. Абсолютная величина вектора ВЗ и подлежит определению в данной работе.

В отсутствие тока I магнитная стрелка ориентируется вдоль вектора ВЗ. Так устанавливается его направление. Затем виток поворачивают таким образом, чтобы вектор ВЗ оказался в его плоскости. После этого по витку пропускают ток в направлении, указанном на рисунке. Оказавшись под одновременным воздействием двух взаимно перпендикулярных полей Вк и ВЗ, магнитная стрелка поворачивается в направлении их суммы, т. е. в направлении вектора В = Вк + ВЗ. При этом угол поворота (a), как видно из рис. 1, удовлетворяет условию