ВУЗы по физике
Готовые работы по физике
Как писать работы по физике
Примеры решения задач по физике
Решить задачу по физике онлайнИспользование закона Био-Савара и принципа суперпозиции
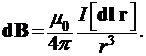
Здесь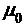 
= 4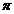
∙10-7 Гн/м – магнитная постоянная, 
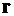– радиус-вектор, проведенный от элемента тока в точку наблюдения. Индукция магнитного поля 
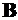, созданного всем током I может быть найдена суммированием полей , созданных в точке наблюдения всеми элементами этого тока. Такой способ расчета опирается на принцип суперпозиции: магнитное поле, создаваемое несколькими токами, равно векторной сумме магнитных полей, создаваемых каждым током в отдельности. Таким образом, полное поле в точке наблюдения есть
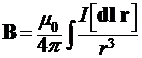. (1)
Использование закона Био-Савара и принципа суперпозиции позволяет рассчитать значения индукции магнитного поля 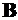в любой точке на оси катушек, что является задачей эксперимента. Лабораторная аппаратура позволяет измерить величину индукции 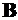поля катушек в определенных точках и сравнить расчетные данные с экспериментальными.
В приложении показано, что величина индукции поля на оси катушки в произвольной точке с координатой x, отсчитываемой от 
(центр катушки), дается выражением
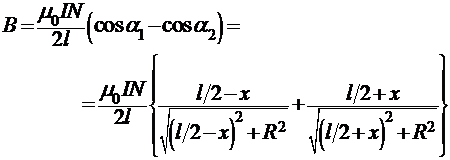(2)
Здесь N – число витков катушки, l – ее длина, x – координата точки наблюдения на оси катушки, R – радиус катушки, 
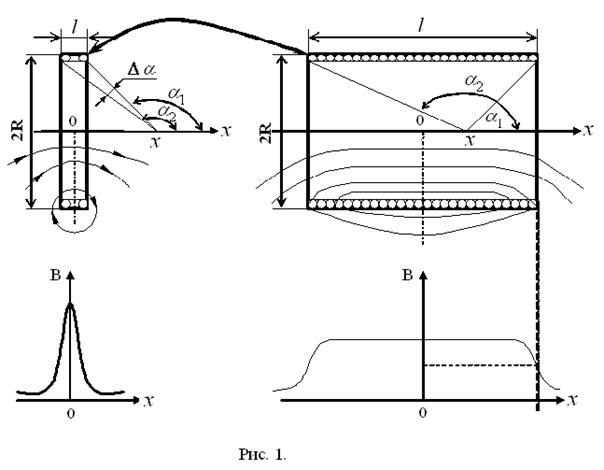
и 
– углы между осью катушки и лучами из точки x к краям катушки (рис. 1).
Примерная картина структуры и величины магнитного поля внутри короткой и длинной катушек приведена на рис. 1.
Если выполняется соотношение 2R l (длинную катушку называют соленоидом), то в точке с координатой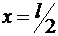 
(торец) имеют место равенства α1=
и α2
, а в центре соленоида (x= 0) — α1
и α2 . В этом случае расчет величины магнитной индукции на оси соленоида в центре Вц и в торце Вт по формуле (2) дает
(3)
где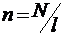 
— число витков на единицу длины соленоида.
Если выполняется соотношение l 2R (короткая катушка) и 
, то с учетом того, что α2 = α1+ ; и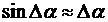 
, получаем
(4)
Из геометрических построений на рис. 1 следует, что
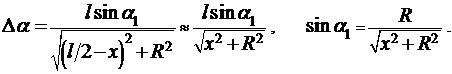(5)
Подставляя (5) в (4), а (4) в (2), получаем окончательную формулу для
магнитной индукции на оси короткой катушки
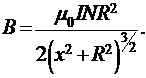(6)
Порядок выполнения работы и вывод расчетных зависимостей
Принципиальная схема установки приведена на рис. 2. Установка состоит из лабораторного модуля 1, миллиамперметра 3, милливольтметра 4 и выносного элемента 5.
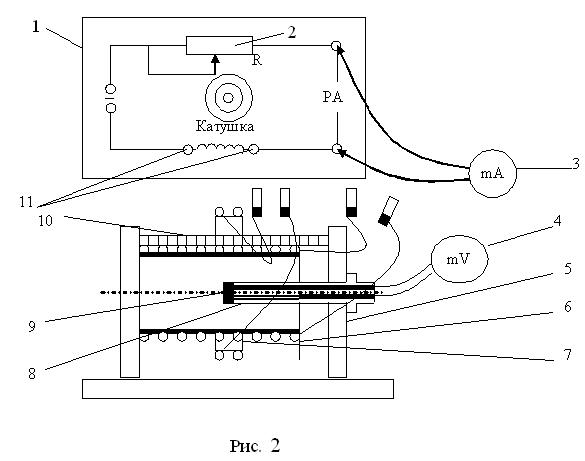
Выносной элемент включает в себя соосно смонтированные на подставке длинную 6 и короткую 7 катушки. В процессе работы они могут быть поочередно присоединены к лабораторному модулю. Модуль служит для обеспечения электропитания выносного элемента. На панели модуля изображена принципиальная электрическая схема, а также установлены гнезда 11 для штекеров короткой и длинной катушек. На катушки подается переменное напряжение частотой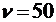 
Гц. Для регулирования силы тока в цепь включен резистор R с переменным сопротивлением. Миллиамперметр, измеряющий ток в катушке, подключен через гнезда «РА» на панели лабораторного модуля. При прохождении через катушку переменного тока возникает переменное магнитное поле.
В качестве датчика магнитной индукции используется измерительная рамка 9, расположенная вблизи катушек на штоке 8, для удобства определения координаты рамки на штоке имеются сантиметровые деления. Через шток выведен коаксиальный кабель, с помощью которого измерительная рамка присоединяется к милливольтметру. Короткая катушка находится на стержне 10 и может передвигаться вдоль него. Положение катушки определяется с помощью сантиметровых делений на стержне.
Под действием переменного магнитного поля катушки в измерительной рамке возникает ЭДС индукции. Так как сопротивление милливольтметра, подключенного к измерительной рамке, довольно велико (не менее 1 МОм), можно считать, что измеряемая милливольтметром раз-ность потенциалов будет равна ЭДС индукции. Ток в катушке изменяется по гармоническому закону, поэтому магнитная индукция в любой точке изменяется во времени по тому же закону 
, где 
—амплитудное значение магнитной индукции, Тл;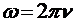 
— циклическая частота, рад/с.
Измерительная рамка располагается так, что плоскость ее витков перпендикулярна линиям индукции. Радиус рамки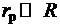 
, поэтому поле в пределах рамки можно считать однородным в каждый момент времени. Магнитный поток сквозь рамку Ф = BSр, где Sр – площадь рамки, м2.
В соответствии с законом индукции Фарадея в рамке наводится ЭДС, мгновенное значение которой
где Np — число витков измерительной рамки.
Учитывая характер изменения магнитной индукции во времени, получаем
Где 
– амплитудное значение ЭДС в вольтах..
Таким образом, магнитная индукция однозначно связана с ЭДС, возникающей в рамке,
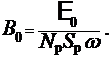(7)
Помещая измерительную рамку в различные точки на оси катушки и измеряя величину возникающей ЭДС индукции, находят распределение магнитной индукции вдоль оси.
Необходимые для расчетов характеристики приведены в табл. 1. В ней величины с индексом «с» относятся к соленоиду, а с индексом «к» к короткой катушке.
Таблица 1
|
Nc |
Nк |
Np |
Rc ,мм 
Рефераты по физике сдают здесь
Другие статьиПохожая информацияУзнать стоимость за 15 минут
Распродажа дипломных
Подпишись на наш паблик в ВК
Нужна работа?
|
МГМИМО
Скидка 30% по промокоду Diplom2020
Получи промокод на скидку 20%
Дипломная работа