Монохроматическая плоская волна

Теперь найдем вектор напряженности магнитного поля. Для этого с учетом того, что 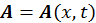запишем векторное произведение и :

Перейдя к переменным светового конуса, можно записать компоненты вектора напряженности магнитного поля:

Скалярное произведение напряженностей электромагнитного поля равно нулю.

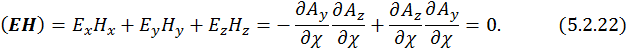
Выражение (5.2.22) – условие ортогональности 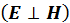. Существует еще условие поперечности:

где – единичный вектор, направленный вдоль распространения волны ().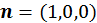

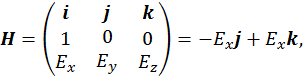
следовательно,

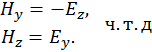
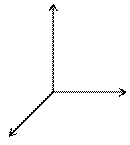
Векторы 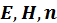направлены по правилу буравчика, как показано на рис.

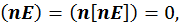
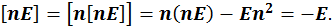
В связи с этим оба инварианта электромагнитного поля лоской

волны обращаются в 0.

Запишем инварианты для напряженностей электромагнитных полей:

т. к. .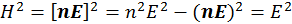

Найдем количество энергии, переносимое плоской волной в единицу времени через единицу площади, она определяется вектором Пойнтинга:

Плотность энергии электромагнитного поля равна:

Следовательно, вектор Пойнтинга (5.2.26) запишется следующим образом:

Откуда следует, что энергия волны распространяется со скоростью света вдоль направления распространения волны, перпендикулярно фронту.

§ 5.3. Монохроматическая плоская волна

а) Потенциалы и напряженности полей.

В плоской волне все величины зависят только от одной координаты (например, х) и времени. Причем, если волна распространяется слева направо вдоль оси Х, то все полевые величины будут зависеть от переменной светового конуса : 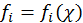, где .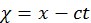

Если зависит от по закону синуса или косинуса, то такая плоская волна называется монохроматической:

где – размерный коэффициент, т. к. косинус должен зависеть от безразмерной величины, а имеет размерность длины. Подставляя значение в (5.3.1), получим

Обозначим 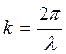– обратная длина. Коэффициент показывает, сколько раз длина волны укладывается на отрезке длиной . – волновое число, связанное с частотой:

откуда видно, что

Формула (5.3.2) перепишется в виде

Надо проверить, что потенциал 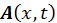удовлетворял волновому уравнению:

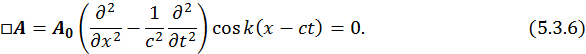
Все предыдущие определения верны только тогда, когда

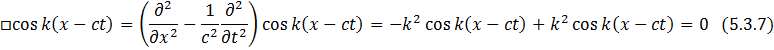
То есть можно считать, что такие волны существуют.

Для плоской монохроматической волны уравнение выполняется. Однако, мы это доказали для одной инерциальной системы отсчета, но это уравнение должно выполняться и в других инерциальных системах отсчета. Согласно принципу Относительности в любой инерциальной системе отсчета все уравнения движения должны иметь одинаковый вид. Имеем: