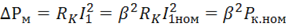Приведение вторичной обмотки трансформатора к первичной

При такой трактовке функций обмоток ЭДС направлена против положительного направления тока , а положительное направление тока вторичной обмотки совпадает по направлению с ЭДС .

В комплексной форме уравнения, составленные по второму закону Кирхгофа, запишутся:

для первичной обмотки

,

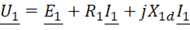для вторичной обмотки

,

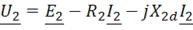где , — падение напряжения на активных сопротивлениях первичной и вторичной обмоток соответственно;

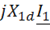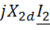, – падение напряжения на сопротивлениях рассеяния первичной и вторичной обмоток соответственно.

6.4. Приведение вторичной обмотки трансформатора к первичной.

При расчете электрической цепи с трансформатором задача расчета усложняется из-за магнитной связи первичной и вторичной обмоток трансформатора. Для устранения магнитной связи составляется эквивалентная электрическая схема, когда обе обмотки объединяют в одну, сделав равными ЭДС (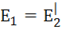) этих обмоток. Равенство будет выполнено, если число витков вторичной обмотки сделать равным числу витков первичной обмотки , т. е. 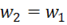. При этом необходимо пересчитать все величины вторичной обмотки – привести вторичную обмотку к числу витков первичной обмотки, в этом случае трансформатор называется приведенным.

Для него МДС, относительные значения падений напряжения и мощность потерь в проводах остается неизменным, т. е.

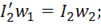
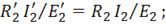
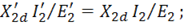
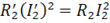
Математически приведенный трансформатор описывается уравнениями электрического состояния

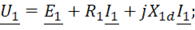
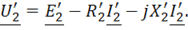
и уравнением токов.

Уравнение токов получим из уравнения МДС для мгновенных значений

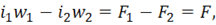
где F – мгновенное значение результирующей МДС обеих обмоток.

При неизменном напряжении на первичной обмотке U1, магнитный поток Ф практически неизменен в режимах холостого хода до номинального. Поэтому можно записать, что

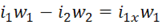
или в комплексном виде

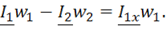
Разделив обе части уравнения на w1 и обозначив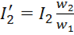, получим уравнение токов

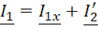
В соответствии с этими уравнениями схема замещения трансформатора выглядит следующим образом (рис. 6.3)

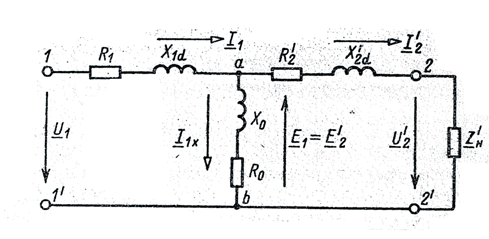
Рис. 6.3

На представленной схеме R1 и – активные сопротивления первичной и вторичной обмоток; X1d и – сопротивления рассеяния первичной и вторичной обмоток; R0, X0 – активное и реактивное сопротивления ветви холостого хода. Падение напряжения на ветви холостого хода с комплексным сопротивлением 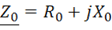при токе равно ЭДС и трансформатора.

Из-за трудности экспериментального определения параметров схемы замещения для расчетов можно использовать упрощенную схему замещения (если пренебречь током холостого хода) (рис. 6.4)

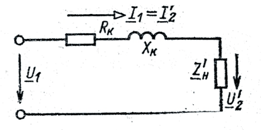
Рис. 6.4

В этой схеме Rk и Xk – сопротивления короткого замыкания 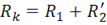и .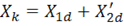

6.1.5. Мощность потерь и КПД трансформатора

Уравнение баланса мощности в цепи с трансформатором

,

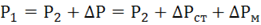где – активная мощность поступающая от источника, 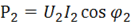– активная мощность потребителя; 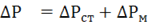— суммарная мощность потерь в трансформаторе; – мощность потерь в стали; – мощность потерь в проводах обмотки.

КПД трансформатора

.

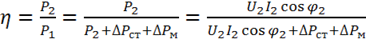Так как коэффициент нагрузки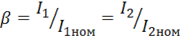, а из опытов короткого замыкания и холостого хода получено, что