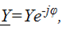задачи по электротехнике и электронике

то в конденсаторе появится электрический ток, сопровождаемый движением зарядов q, пропорциональных приложенному напряжению:

,

где С – коэффициент пропорциональности, называемый емкостью.

При этом

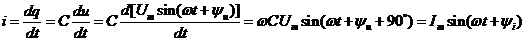— ток тоже синусоидальный,

где 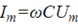– амплитуда тока;

I=ωCU – действующее значение тока;

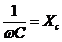— емкостное сопротивление.

Начальная фаза тока 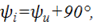откуда сдвиг фаз 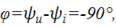т. е. ток на 90̊ опережает приложенное к емкостному элементу напряжение (рис.3.7, б, с).

Заменим мгновенные значения тока и напряжения их комплексными выражениями:

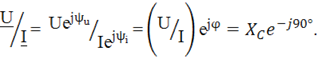
Закон Ома в комплексной форме для участка цепи с емкостным элементом запишется:

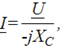
где — емкостное сопротивление в комплексной форме, представляющее собой отрицательное мнимое число.

Для закрепления материала предлагается решить следующие задачи:

Задача 3.5.

Определить сопротивление XC, если действующее значение напряжения U = 220В, а ток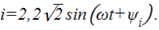

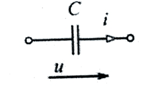
Задача 3.6.

Определить сдвиг фаз между током I и напряжением 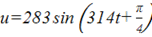в цепи, где R=20 Ом.

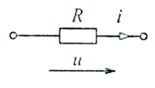
Задача 3.7.

Определить индуктивное сопротивление ХL, при частоте тока f=50Гц и индуктивности L=0,239Гн

3.4. Цепи синусоидального тока при последовательном соединении элементов.

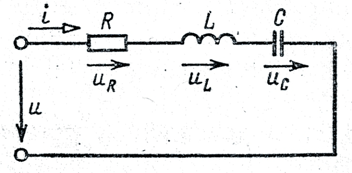
Рис. 3.8

Если к участку цепи с последовательным соединением элементом R, L, C (рис.3.8)приложить синусоидальное напряжение 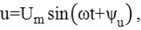то ток в цепи синусоидальный 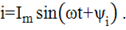По второму закону Кирхгофа:

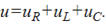
Заменив мгновенные значения их комплексными выражениями, получим:

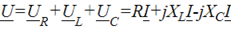
Закон Ома для данного участка цепи запишется:

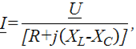
где 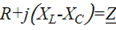– комплексное сопротивление участка цепи,

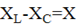– реактивное сопротивление.

В показательной форме:

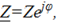
где 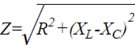— модуль комплексного сопротивления, которое называется полным сопротивлением цепи;

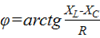– аргумент комплексного сопротивления.

Решить задачи:

Задача 3.8.

Определить комплексное сопротивление Zцепи, где R=6 Ом, ХС=8 Ом.

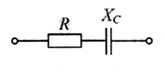
Задача 3.9.

Определить полное сопротивление Z цепи, в которой R=3 Ом, ХL=4 Ом.

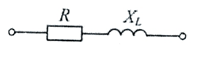
Задача 3.10.

В приведенной цепи R1=2 Ом, R2=1 Ом, XL1=1 Ом, XL2=3 Ом. Определить полное сопротивление Z этой цепи.

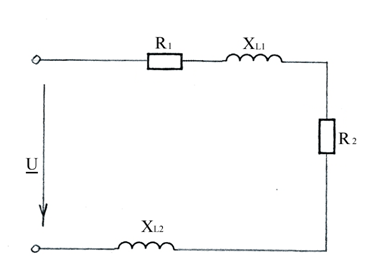
Задание 3.11.

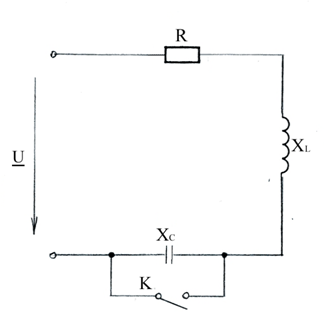
Как изменится ток в цепи при замыкании ключа К, если XC=2XL и U остается неизменным?

3.5. Цепь синусоидального тока при параллельном соединении элементов (рис.3.7)

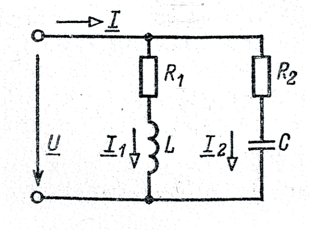
Рис 3.9

Из первого закона Кирхгофа для схемы рис. 3.9, следует:

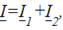
где — токи в параллельных ветвях,

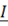– общий ток.

Для каждого тока по закону Ома запишем:

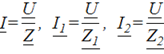
И тогда уравнение по первому закону Кирхгофа перепишется:

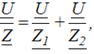
откуда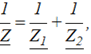

и полное сопротивление всей цепи

где 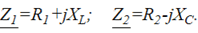–комплексные сопротивления ветвей.

Заменим сопротивления ветвей через их проводимости:

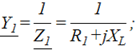
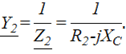
Тогда комплексная проводимость всей цепи будет равна:

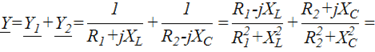
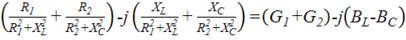==G—jB

В показательной форме