ВУЗы по физике
Готовые работы по физике
Как писать работы по физике
Примеры решения задач по физике
Решить задачу по физике онлайнНеопределенность энергии и время жизни
Для примера рассмотрим распады. Среди лептонов самым легким является электронное нейтрино. Это — стабильная частица, так как любой распад запрещен законом сохранения энергии. Продуктами распада должны быть более легкие лептоны, причем, закон сохранения лептонного заряда требует, чтобы одна из распадных частиц имела электронный лептонный заряд. А так как более легких лептонов, чем нейтрино, нет, то распад нейтрино запрещен. В природе он и не происходит. Электрон более тяжелый лептон, чем нейтрино, поэтому закон сохранения энергии не запрещает его распад. Тем не менее, электрон является стабильной частицей. Распад запрещен законом сохранения электрического заряда — из заряженных лептонов электрон является самым легким. Распад мюона не запрещен ни законом сохранения энергии, ни законом сохранения лептонного заряда, поэтому он является нестабильным. Существует единственный способ распада (мода распада): 
(7)
Значком “тильда – ~” обозначаются античастицы. В левой части электрический заряд равен минус единице (одному элементарному заряду), мюонный лептонный заряд равен единице. В правой части электрический заряд также равен минус единице. Электронные лептонные заряды электрона и электронного антинейтрино взаимно уничтожаются, так что в сумме получается нуль. Мюонное нейтрино дает равный единице мюоный лептонный заряд. Все законы сохранения выполняются.
Задача 3. Используя законы сохранения, объясните, почему протон является стабильной частицей, а нейтрон имеет возможность распасться. На какие частицы распадается нейтрон?
Задача 4. Покажите, что свободный фотон ни при какой энергии не может распасться. Какой закон сохранения будет обязательно нарушен? Почему вблизи какого либо ядра возможно взаимодействие g®e++e—?
Пример. Рассмотрим два почти неотличимых взаимодействия p-+p® L0+K0 и . При энергии, превышающей порог взаимодействия, первое возможно, а второе ни при какой энергии невозможно. Все дело в том, что данные взаимодействия являются адронными. В адронных взаимодействиях странность должна сохраняться. В левых частях суммарная странность равна нулю. В правых же частях: в первом взаимодействии суммарная странность также равна нулю, а во втором суммарная странность равна –2. Во втором взаимодействии странность не сохраняется. Это обстоятельство налагает запрет на данное взаимодействие — оно невозможно.
Пример. Распад нейтрального каона на пару пионов K0®p++p— возможен, хотя странность не сохраняется. Причина состоит в том, что это взаимодействие является слабым. А в слабых взаимодействия допускается несохранение странности.
2.4 Упражнения для самостоятельной работы
Задача 5. Определите, какие взаимодействия могут идти, а какие — нет. Почему?
1. e++e—® g;
2. K-+p ®S-+ p+;
3. K-+p ®Lo+ p+;
4. K-+p®Lo +po;
5. p-+p®S— +p+;
6. p-+p®Lo +Ko;
7. Ko+p®Lo+p+;
8. K-+p®p+K— +po;
9. K-+p®p +p-;
10. nm +p®n+m+;
11. 
+ p®po +p+;
12. +p®K-+p +p+;
Задача 6. При рассеянии нейтрино высокой энергии, получающихся при распаде пионов на лету по схеме 
на протонах рождаются две частицы. Одна из них нейтрон.
а) Какая вторая частица?
б) Какой результат этого эксперимента подтверждает закон сохранения лептонного числа?
в) Следует ли из данного эксперимента, что электронное и мюонное нейтрино являются разными частицами?
Задача 7. При рассеянии фотонов подходящей энергии на атомах возможно поглощение атомом фотона и переход атома в возбужденное состояние. Аналогичное явление наблюдается при рассеянии фотонов на протонах: фотон поглощается, а протон переходит в возбужденное состояние, превращаясь в D-резонанс. О чем говорит тот факт, что такое никогда не происходит при рассеянии фотонов на электронах?
3. Домашнее задание
3.2 Решение задач
Задача 1. Возможны ли следующие взаимодействия:
1. K—+p®p+K—+p++po+p—?
2. K—+p ®K—+ p+p—?
3. K—+p ®K—+p+po?
4. p+p®Lo+ e++e—?
5. p+p®Lo+p+e++ne?
6. ne+p®Ko+e++Lo?
7. e++e—® p+ ?
8. m—®Lo+
+nm?
Задача 2. На покоящийся протон налетает отрицательный пион. При каком минимальном значении кинетической энергии пиона возможно взаимодействие
p-+p®Lo+Ko?
Значения инвариантных масс участвующих во взаимодействии частиц см. в таблице.
занятие 2.3.3
Обменное взаимодействие
2. Повторение принципа неопределенностей
2.1 Неопределенность координаты и импульса
Центральными в квантовой механике являются понятие амплитуды вероятности и принцип суперпозиции состояний. Описание состояний частиц с помощью амплитуд вероятности говорит о том, что в каждый момент времени точечная частица занимает сразу некоторую область пространства. Связанное состояние частицы описывается локализованным в ограниченной области пространства распределением амплитуд вероятности. Такому распределению отвечает некоторый размер области локализации Dx.
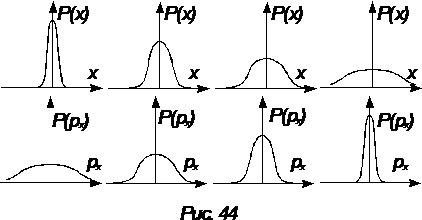Частица, находящаяся в локализованном состоянии, не имеет определенного значения импульса. Если проводить измерения импульса локализованной частицы, результатами эксперимента будут являться случайные значения, распределенные около нуля. Разброс измеряемых значений импульса Dpx тем больше, чем в меньшей области локализовано распределение амплитуды вероятности. В этом состоит принцип неопределенностей. На рисунке 44 изображены графики распределений вероятности координаты частицы (вверху) и значений импульса в том же состоянии (внизу). Математическое выражение принципа имеет вид
Dpx Dx~ћ /2. (1)
Из принципа неопределенности в частности следует, что для того, чтобы локализовать положение частицы, надо совершить работу.
Задача 1. Частица массы m находится в непроницаемом ящике размером L, с подвижной стенкой. Используя принцип неопределенностей оцените увеличение энергии частицы при уменьшении размера ящика путем перемещения подвижной стенки на dL. Используя полученный результат, найдите силу, с которой частица действует на стенку.
Локализованная частица создает давление на тела, которые ограничивают область расположения частицы (гайзенберговское давление). В атоме электронное давление компенсируется силой притяжения к ядру. В ядре из-за сильной локализации нуклонов гайзенберговское давление чрезвычайно велико, поэтому только мощное адронное притяжение способно удерживать его от разрыва.
Задача 2. На малых расстояниях ядерное притяжение гораздо сильнее электростатического притяжения разноименно заряженных частиц. Объясните кажущийся парадокс: почему слабое электростатическое притяжение удерживает электрон около протона в атоме водорода, а более сильное ядерное притяжение не способно удержать вместе два нейтрона.
Вопрос 1. Какой из атомов больше: водорода или гелия? Дайте обоснование своему ответу.
2.2 Неопределенность энергии и время жизни
Другое проявление принципа неопределенностей относится к энергии. Допустим, квантовая система находится в распадающемся состоянии (атом в возбужденном состоянии, или радиоактивное ядро). Если среднее время жизни в этом состоянии равно Dt, то энергия системы в данном состоянии определена с ограниченной точностью DE. Причем
DE Dt ~ћ. (2)
Это проявляется в том, например, что длина волны излучаемого атомом света не является строго определенной. Причина состоит в том, что энергия излучаемого фотона равна разности энергий возбужденного и основного состояний, и из-за неопределенности энергии распадающегося состояния является случайной величиной. С помощью дифракционной решетки хорошего качества можно обнаружить, что спектральные линии всегда в большей или меньшей степени размыты.
МГМИМО
Скидка 30% по промокоду Diplom2020
Получи промокод на скидку 20%
Дипломные