Определение напряжений на площадке произвольного положения
Аналогично
![]()
откуда 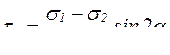 . (6.9)
. (6.9)
Из формулы (6.9) видно, что максимальное касательное напряжение равно полуразности главных напряжений (при 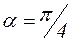 ):
):
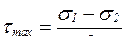 . (6.10)
. (6.10)
Из формул (6.8) и (6.9) следует:
1. Если ![]() , то на всех площадках, проходящих через рассматриваемую точку, нормальное напряжение равно
, то на всех площадках, проходящих через рассматриваемую точку, нормальное напряжение равно ![]() , а касательное напряжение равно нулю. Такое напряжённое состояние называют равномерным двухосным растяжением (или сжатием).
, а касательное напряжение равно нулю. Такое напряжённое состояние называют равномерным двухосным растяжением (или сжатием).
2. Если ![]() ,
, 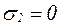 , а
, а 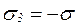 , то при
, то при 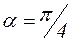 нормальное напряжение в наклонной площадке оказывается равным нулю, а
нормальное напряжение в наклонной площадке оказывается равным нулю, а 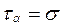 . Такое напряжённое состояние называется чистым сдвигом.
. Такое напряжённое состояние называется чистым сдвигом.
6.4. Определение напряжений на площадке произвольного
положения
Пусть у некоторой выбранной точки D тела наблюдается плоское напряжённое состояние (рис. 33а, б).
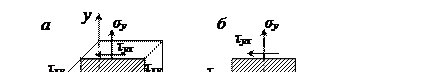 Выделим в окрестности точки призму abca’b’c’ (рис. 33в), на грани bb’с′с которой (рис. 33г) действует нормальное напряжение σα и касательное τα (п – нормаль к этой грани, t – касательная). Рассмотрим равновесие данной призмы, приняв площадь наклонённой грани bb’с’с за dА. Тогда площадь грани abb’a’, перпендикулярной оси х – dAcosα, а грани aa′c′c, перпендикулярной оси у – dAsinα. На грани abb’a’, относительно которой на угол α повернута площадка bb’с′с, направление касательного напряжения τху = τ принято положительное.
Выделим в окрестности точки призму abca’b’c’ (рис. 33в), на грани bb’с′с которой (рис. 33г) действует нормальное напряжение σα и касательное τα (п – нормаль к этой грани, t – касательная). Рассмотрим равновесие данной призмы, приняв площадь наклонённой грани bb’с’с за dА. Тогда площадь грани abb’a’, перпендикулярной оси х – dAcosα, а грани aa′c′c, перпендикулярной оси у – dAsinα. На грани abb’a’, относительно которой на угол α повернута площадка bb’с′с, направление касательного напряжения τху = τ принято положительное.
Сумма проекций всех сил на нормаль п:
Приняв τху= τух= τ и сократив на dА, получим формулу для определения нормальных напряжений на площадке bb’с′с:
![]() . (6.11)
. (6.11)
Проецируя все действующие силы на направление касательной t к наклонной площадке, получим:
![]() .
.
После несложных преобразований получим формулу для определения касательных напряжений на площадке bb’с′с:
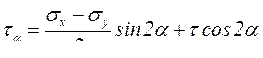 . (6.12)
. (6.12)
Формула для определения положения главных площадок, т. е. площадок, на которых касательные напряжения равны нулю, следует из выражения (6.12) при 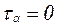 :
:
 . (6.13)
. (6.13)
Углы α0 и  , найденные по формуле (6.13), определяют положение главных площадок около анализируемой т. А. Подстановкой найденных значений углов α0 и
, найденные по формуле (6.13), определяют положение главных площадок около анализируемой т. А. Подстановкой найденных значений углов α0 и  в выражение (6.11) для напряжений σα получим значения главных напряжений (σ2 = 0):
в выражение (6.11) для напряжений σα получим значения главных напряжений (σ2 = 0):
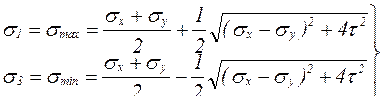 . (6.14)
. (6.14)
Максимальное значение касательных напряжений в теле:
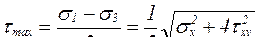 . (6.15)
. (6.15)
Значение ![]() возникает на площадке, параллельной вектору
возникает на площадке, параллельной вектору ![]() и делящей пополам угол между первой и третьей главными площадками.
и делящей пополам угол между первой и третьей главными площадками.
6.4. Теории прочности
При центральном растяжении (сжатии) в нормальных сечениях стержня возникают одни нормальные напряжения ![]() . Условие прочности в данном случае имеет вид:
. Условие прочности в данном случае имеет вид:
![]() .
.
Здесь допускаемое напряжение ![]() вполне определяется механическими испытаниями материала на растяжение (сжатие) и условиями работы детали.
вполне определяется механическими испытаниями материала на растяжение (сжатие) и условиями работы детали.
Если в рассматриваемом сечении имеются одни касательные напряжения ![]() (чистый сдвиг), то условие прочности запишется так:
(чистый сдвиг), то условие прочности запишется так:
![]() ,
,
где ![]() определяется механическими испытаниями материала на сдвиг (срез) и условиями работы детали.
определяется механическими испытаниями материала на сдвиг (срез) и условиями работы детали.
Оценку прочности конструкции в точке в случае сложного напряжённого состояния, когда в данной точке на данной площадке одновременно действуют ![]() и
и ![]() , произвести на основании эксперимента весьма затруднительно. Для такой оценки прочности деталей служат теории прочности, которые строятся на основе различных критериев прочности. Критерий прочности устанавливается на основании гипотез возникновения текучести материала или его разрушения (гипотез предельных состояний). Предельное напряжённое состояния в общем случае зависит от соотношения между тремя главными напряжениями. Гипотезы предельных состояний (гипотезы прочности) основываются на предпосылке, что два каких-либо напряжённых состояния считаются равноопасными, если они, при увеличении главных напряжений в одно и то же число раз, одновременно становятся предельными. В этом случае коэффициент запаса прочности для обоих напряжённых состояний в указанных условиях будет одинаковым.
, произвести на основании эксперимента весьма затруднительно. Для такой оценки прочности деталей служат теории прочности, которые строятся на основе различных критериев прочности. Критерий прочности устанавливается на основании гипотез возникновения текучести материала или его разрушения (гипотез предельных состояний). Предельное напряжённое состояния в общем случае зависит от соотношения между тремя главными напряжениями. Гипотезы предельных состояний (гипотезы прочности) основываются на предпосылке, что два каких-либо напряжённых состояния считаются равноопасными, если они, при увеличении главных напряжений в одно и то же число раз, одновременно становятся предельными. В этом случае коэффициент запаса прочности для обоих напряжённых состояний в указанных условиях будет одинаковым.
Поэтому в случае сложного напряжённого состояния следует определить эквивалентное напряжение, при котором возникает опасность разрушения, и сравнить его с допустимым значением напряжения на растяжении, полученным опытным путём:
![]() .
.
Существует несколько гипотез прочности. Одни гипотезы прочности дают удовлетворительные результаты для хрупких материалов, другие – для пластичных.
Рассмотрим наиболее известные теории прочности в хронологическом порядке их появления.
1. Теория наибольших нормальных напряжений (первая теория прочности). В XVIII–начале XIX в. преимущественно применялись такие материалы, как камень, стекло, кирпич, чугун, т. е. хрупкие материалы. Для них наиболее свойственным представлялось разрушение путём отрыва. Поэтому согласно первой теории прочности считалось−разрушение материалов при сложном напряжённом состоянии наступает тогда, когда наибольшее нормальное напряжение достигает предельного значения.
Условие прочности по этой теории для расчетного (или эквивалентного) напряжения имеет вид
σр = σэквI = σ1 ≤ [σ], (6.16)


