Опыты томсона и тартаковского

Из последнего выражения видно, что дифракцию можно наблюдать двумя способами:

1.При постоянном ускоряющем напряжении (и, соответственно ) изменять угол , поворачивая либо кристалл, либо коллектор.

2.Проводить измерения при , изменяя разность потенциалов и, следовательно, де-бройлевскую длину волны электрона.

Полученная при фиксированном угле скольжения зависимость имеет несколько максимумов, соответствующих различным значениям .

Если на этом рисунке отложить вычисленные по формуле (**) значения , получим систематическое

отклонение рассчетных значений от эмпирических при

малых (теория дает равноотстоящие максимумы, т. к.

).

В связи с этим Г. Бете предложил электронным

волнам, как и электромагнитным, приписать показатель

преломления: , или через отношение

фазовых скоростей .

В вакууме: ,

(в нерелятивистском приближении ).

В металле:

,

где — глубина потенциальной ямы, в которую попадает

электрон, проникая в металл.

Если ввести потенциалы, то можно записать

,

где внутренний потенциал металла, а кинетическая энергия

электрона, прошедшего ускоряющую разность потенциалов , равна .

Тогда

.

Отсюда получаем, что относительный показатель преломления среды равен

, .

Разность хода интерферирующих лучей получаем

из рассмотрения простой геометрической задачи.

; ;

; ;

.

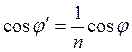С учетом преломляющих свойств кристалла условие Брэгга-Вульфа принимает вид , или окончательно

.

Введение показателя преломления среды при описании распространения волн де-Бройля позволяет достичь полного согласия с экспериментом (в пределах точности эксперимента).

2) Опыты Томсона и Тартаковского.

В 1928 г. Дж. П.Томсон (1892-1975), а также П. С.Тартаковский (1895-1932) наблюдали дифракционную картину при прохождение электронов через тонкие пленки (фольгу, слюду), используя метод, предложенный Дебаем и Шерером для исследования поликристаллических материалов с помощью рентгеновских лучей.

Суть эксперимента состоит в следующем. Узкий

пучок моноэнергетических электронов, ускоренных

разностью потенциалов в несколько киловольт

,

направляется на исследуемый образец, толщина

которого составляет . Проходя через

образец, который равномерно вращается вокруг оси

пучка, электроны рассеиваются на различные углы.

Рассеянные электроны попадают на фотопластинку.

Поликристаллический образец представляет собой

совокупность хаотично ориентированных монокристаллов, среди множества которых найдутся такие, при отражении от которых для де-бройлевской волны выполняется условие Брэгга-Вульфа.

Полученная таким образом электронограмма золота (рис. а) обнаруживает поразительное сходство с полученной в аналогичных условиях рентгенограммой алюминия (рис. б).

Т. о., эксперименты показали, что прохождение электронов сквозь тонкие пленки сопровождается появлением характерной дифракционной картины точно такого же вида, что и рентгеновские интерференционные кольца Дебая-Шерера.

Зная диаметр кольца и расстояние до экрана, можно найти постоянную кристаллической решетки

.

2)  Дифракция атомов и молекул.

В 1930 г. Штерн с сотрудниками установил, что отражение легких атомов и молекул () от поверхности кристалла также сопровождается дифракционными явлениями. Выбор химических элементов был обусловлен длиной де-бройлевской волны, которая, например, для гелия при комнатной температуре составляет , т. е. порядка постоянной

кристаллической решетки. Тепловой разброс

молекул по скоростям устранялся с помощью

селектора скоростей — двух зубчатых колес,

насаженных на одну ось – выделялись близкие

по скорости молекулы. В качестве индикатора

использовался чувствительный манометр.

Положение боковых максимумов относительно

центрального меняется с температурой, т. к.

изменяется де-бройлевская длина волны молекулы

газа.

Открытие Штерна было очень важным и

впечатляющим. Правильность соотношения

де-Бройля для молекулярных пучков была

подтверждена с точностью 1%. А ведь здесь мы

имеем дело уже с материальными частицами, из

которых состоят, как известно, не только газы, но также и жидкости и твердые тела. Если перехватить

пучок, уже претерпевший дифракцию на кристаллической решетке, и направить в сосуд, то мы обнаружим все тот же газ с самыми обычными свойствами.

4) Дифракция нейтронов.

Убедиться в волновой природе вещества можно также, изучая рассеяние нейтронов на решетках кристаллов. Для тепловых нейтронов (нейтронов, энергия которых соответствует температуре ) длина волны де-Бройля равна . Тепловые нейтроны используются в методе Лауэ. Пучок направляется на неподвижный монокристалл, а затем отраженные кристаллическими плоскостями нейтроны в направлениях, определяемых условием Брэгга-Вульфа, образуют, так называемые, пятна Лауэ. Дифракционная картина, возникающая в результате рассеяния нейтронов, дает богатую информацию о кристаллической структуре твердых тел.