Площадь и координаты центра тяжести простейших фигур
Определяем необходимую площадь поперечного сечения стержня:
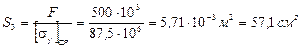
Среднее напряжение и площадь поперечного сечения стержня по сравнению с предыдущим приближением изменилась незначительно. Поэтому, выбирая по таблицам сортамента сечение стержня, мы снова получим двутавр №36. Но так как, по этому двутавру расчет уже производился, то примем двутавр № 33 и подсчитаем величину перенапряжения в стержне. Если перенапряжение не превысит 5%, то окончательно примем двутавр № 33.
По таблицам сортамента для двутавра № 33: S = 53,8 см2, imin = iy = =2,79см.
Находим гибкость стержня:
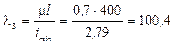 .
.
Определяем коэффициент j4:
j4 = 0,5968.
Определяем допускаемое напряжение на устойчивость:
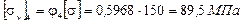 .
.
Определяем рабочее напряжение стержня:
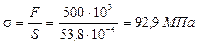 .
.
Сравним рабочее и допускаемое напряжение на устойчивость:
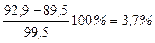
Перенапряжение стержня составило менее, чем 5%, поэтому окончательно принимаем двутавр № 33.
Указания к задаче 9
Часто в строительстве и машиностроении применяются конструкции, состоящие не из отдельных стержней, а из целых систем стержней соединенных между собой. Поэтому необходимо умение вести расчет и таких конструкций.
Система стержней, жестко соединенных между собой называется рамой.
В поперечных сечениях плоских (стержни и нагрузка лежат в одной плоскости) рам действуют три внутренних силовых фактора: нормальная сила N, поперечная сила Q и изгибающий момент M. Поэтому, при расчете рам, для определения опасного сечения, необходимо строить эпюры всех трех В. С.Ф.
Поперечное сечение при проектном расчете рамы подбирается по максимальному изгибающему моменту. Подобранное сечение проверяется по условию прочности:
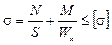 .
.
Задачи расчета на жесткость требуют умения определять деформации и перемещения. Одним из методов определения перемещений в стержневых системах является интеграл Мора, формула которого выглядит следующим образом:
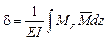 ,
,
где EI – жесткость сечения балки;
MF – уравнение изгибающего момента от внешних сил;
![]() — уравнение изгибающего момента от единичной силы.
— уравнение изгибающего момента от единичной силы.
Для определения перемещений по интегралу Мора нужно:
2.2) Составить уравнение изгибающего момента от внешних сил MF.
3.2) В исследуемой точке приложить только единичную силу F = 1 или единичный момент М = 1.
4.2) Записать уравнения изгибающего момента только от единичной нагрузки ![]() .
.
5.2) Определить перемещения.
Примечание
2.3) Если при определении перемещений получили их со знаком «+», то угадали направление, если получили знак «-», то не угадали.
3.3) Интегрирование проводится по участкам.
Способ Верещагина является графическим решением интеграла Мора. Дадим некоторые определения.
Единичной называется эпюра, построенная от действия единичной силы или единичного момента.
Грузовой называется эпюра, построенная от действия внешних сил.
Формула для определения перемещений по способу Верещагина:
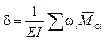 ,
,
где wi — площадь грузовой эпюры;
![]() — ордината, взятая с единичной эпюры под центром тяжести грузовой.
— ордината, взятая с единичной эпюры под центром тяжести грузовой.
Чтобы определить перемещения по способу Верещагина необходимо:
5.1) Построить грузовую эпюру.
6.1) В исследуемой точке приложить единичную нагрузку.
7.1) Построить единичную эпюру.
8.1) Определить прогиб или угол поворота.
Примечание.
5.2) Перемножение производится по участкам.
6.2) ![]() берется только с линейной эпюры.
берется только с линейной эпюры.
7.2) Если обе эпюры линейные (ограниченные прямыми), то перемножение можно вести в обратном порядке.
8.2) Если значение перемещения получится со знаком «+», то угадали направление перемещения, если получится знак «-», то не угадали.
Площадь и координаты центра тяжести простейших фигур.
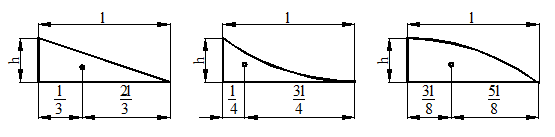
Рисунок 29.
Площадь треугольной эпюры 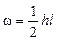 .
.
Площадь эпюры с вогнутой параболой 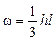 .
.
Площадь эпюры с выпуклой параболой 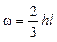 .
.
ПРИМЕР 1
Определить перемещение точки К балки, показанной на рис. 30 при помощи интеграла Мора.
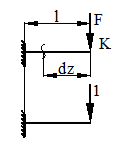
Рисунок 30.
1) Составляем уравнение изгибающего момента от внешней силы MF.
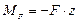
2) Прикладываем в точке К единичную силу F = 1.
3) Записываем уравнение изгибающего момента от единичной силы ![]() .
.
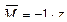
4) Определяем перемещения
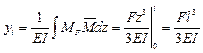
ПРИМЕР 2
Определить перемещение точки К балки, показанной на рис. 31 по способу Верещагина.
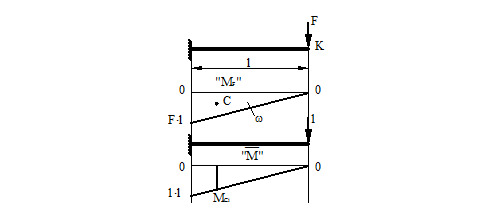
Рисунок 31.
1) Строим грузовую эпюру.
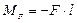
2) Прикладываем в точке К единичную силу.
3) Строим единичную эпюру.
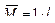
4) Определяем прогиб
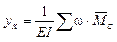
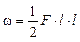 ;
; 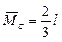 ;
; 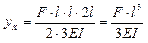
ПРИМЕР 3
Для стальной рамы, показанной на рис. 32 построить эпюры В. С.Ф., подобрать двутавровое поперечное сечение, определить вертикальное перемещение и угол поворота сечения в точке С, если F = 10 кН, q = 4 кН/м, a = 2 м, b = 1м, [s] = 120 МПа.
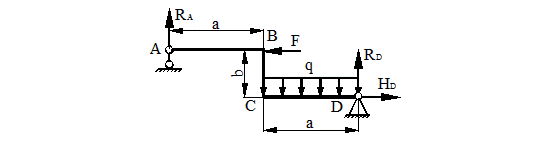
Рисунок 32.
1) Определяем опорные реакции
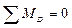 ;
; 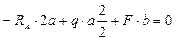
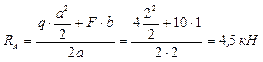
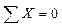 ;
; 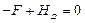
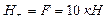
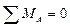 ;
; 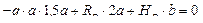
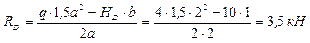
Проверка
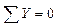 ;
; 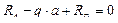
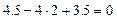 — верно
— верно
2) Строим эпюры В. С.Ф.
Эпюра нормальной силы (рис. 33)
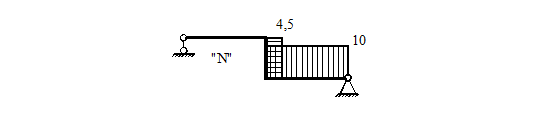
Рисунок 33.
Эпюра поперечной силы (рис. 34)
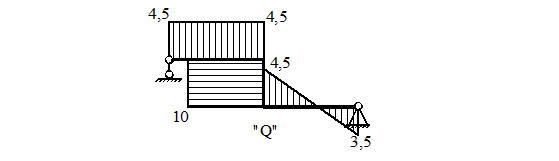
Рисунок 34.
Эпюра изгибающего момента
Составляем уравнения изгибающих моментов для каждого участка рамы.
АВ
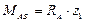
ВС
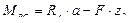
Найдем координату сечения, в котором эпюра изгибающего момента пересекает нулевую линию.
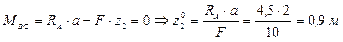
CD
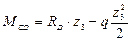
Найдем координату сечения, в котором эпюра изгибающего момента пересекает нулевую линию.
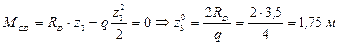
Найдем координату сечения, в котором эпюра изгибающего момента имеет максимум. Для этого найдем производную от изгибающего момента и приравняв ее к нулю выразим z3 max.
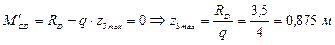
Найдем максимум изгибающего момента.
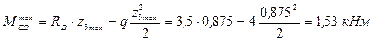
Эпюра изгибающего момента показана на рис. 35.
Максимальный изгибающий момент возникает в т. В, его величина составляет Mmax = 9 кНм. Нормальная сила в этом сечении N = 4,5 кН.
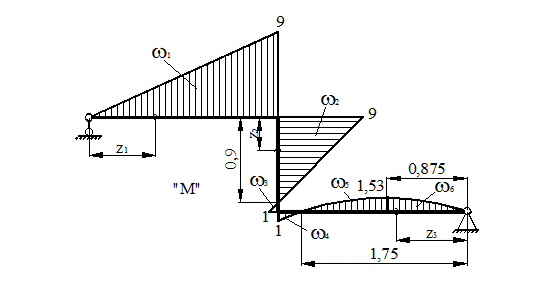
Рисунок 35.
3) Подбираем поперечное сечение
Поперечное сечение подбираем из условия прочности на изгиб:
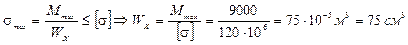
По ГОСТ 8239 – 89 подбираем двутавр № 14: WX = 81,7 см3, IX = 572 см4.
4) Проверяем поперечное сечение по условию прочности
Условие прочности выполняется.
5) Строим единичные эпюры
Эпюра от единичного момента
Определяем опорные реакции от действия единичного момента, схема рамы показана на рис. 36.
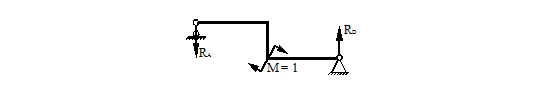
Рисунок 36.
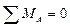 ;
; 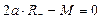
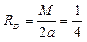 ;
;
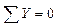 ;
; 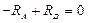
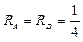
Эпюра представлена на рис. 37.
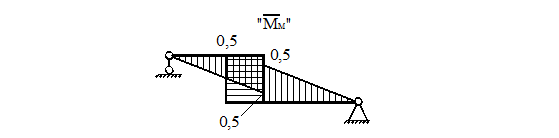
Рисунок 37.
Эпюра от единичной силы
Определяем опорные реакции от действия единичной силы, схема рамы показана на рис. 38.
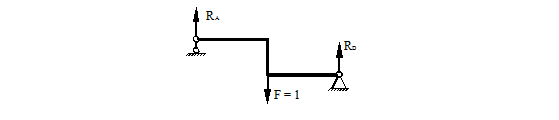
Рисунок 38.
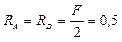
Эпюра представлена на рис. 39.
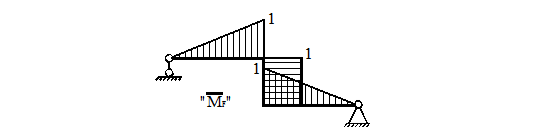
Рисунок 39.
6) Определяем угол поворота т. С
Угол поворота определим по способу Верещагина, перемножив эпюры ![]() и
и ![]() .
.
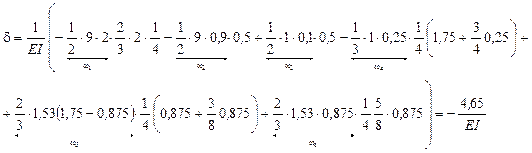
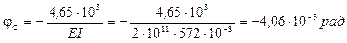
7) Определяем вертикальное перемещение т. С
Перемещение определим, перемножив эпюры ![]() и
и ![]() .
.
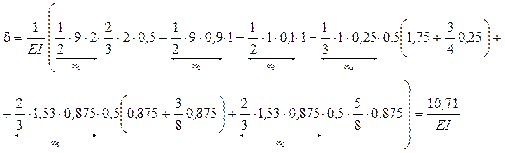

Указания к задаче 10
Под ударом понимается взаимодействие двух движущихся тел в результате их соприкосновения, связанное с резким изменением скоростей этих тел, за весьма малый промежуток времени. При ударе нагрузки и напряжения резко возрастают sуд >> sст. Теория удара опирается на некоторые допущения: форма изогнутой оси балки при ударе подобна изогнутой оси балки при статическом ее нагружении; считают, что удар является неупругим, то есть ударяющее тело не отскакивает от конструкции, а продолжает двигаться вместе с ней; считают, что деформации, вызванные ударом, являются упругими, то есть smax уд < sпц; массой балки пренебрегают, то есть считают балку невесомой. При расчетах на удар определяют максимальные напряжения и максимальные деформации по формулам:


