Плоские электромагнитные волны

Теперь найдем волновые уравнения для напряженностей электрических и магнитных полей:

Если подействовать вектором в векторном произведении на волновое уравнение, то получим:

Таким образом, все уравнения для полевых величин имеют одинаковый вид. Т. е. если 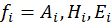, то волновое уравнение имеет вид: .

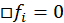§ 5.2. Плоские электромагнитные волны

Если полевые величины зависят от одной координаты и времени, то такие электромагнитные волны называются плоскими. В этом случае фронт такой волны является плоским.

Рассмотрим волновое уравнение для плоских электромагнитных волн в кулоновской калибровке, оно имеет вид:

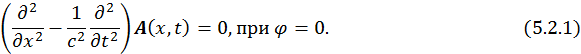
Это уравнение можно переписать в следующем виде (для того, чтобы найти его решение):

Для нахождения решения уравнения (5.2.2) введем новые переменные – переменные светового конуса:

Обратные соотношения выглядят следующим образом:

Запишем наше волновое уравнение в переменных светового конуса, для этого необходимо установить связь производных:

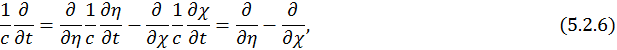
следовательно,

Перемножая (5.2.7) и (5.2.8), получим, что

Найдем решение этого уравнения, проинтегрируем (5.2.9) по , тогда

Проинтегрировав выражение (5.2.10), получим:

где – первообразная от . Решением однородного волнового уравнения является сумма двух произвольных функций от одной из переменных светового конуса. Выясним смысл этих произвольных функций. С этой целью зафиксируем момент времени t=const. Тогда получим волну. Если наоборот, зафиксировать координату x=const, то в этой точке будут колебания поля. А если зафиксируем 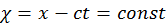, то для этой переменной функция 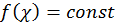, т. е. поле остается постоянным. Точка 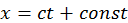– точка, которая распространяется со скоростью света в положительном направлении оси X ( – фаза).

Т. е. точка с постоянной фазой распространяется слева направо с одинаковой скоростью – скоростью света. Если зафиксировать 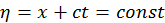, то точка 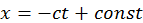будет двигаться в сторону, противоположную направлению оси X.

Замечание: Фазовая скорость может быть больше скорости света.

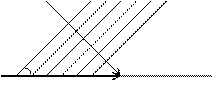фронт волны

Пусть волна падает под углом α (см. рис.). По оси Х скорость

с Х больше скорости света:

Фазовая скорость не является скоростью движения, связанной с материальным объектом.

Найдем напряженности электромагнитных полей в плоской волне.

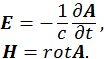
Для одной координаты и времени эти соотношения запишутся следующим образом:

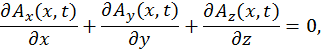
откуда видно, что

Это ограничение, вследствие которого волновое уравнение для х-компоненты векторного потенциала (5.2.1) примет вид:

Напряженность электрического поля в этом случае выглядит так:

и, следовательно,

Таким образом, получаем, что – постоянная во времени величина. А т. к. это произвольная постоянная, то положим =0, т. к. напряженности полей электромагнитных волн обязательно должны зависеть от времени. Следовательно, у электромагнитных волн нет продольной составляющей.

В терминах светового конуса остальные компоненты напряженности электрического поля в электромагнитной волне запишутся следующим образом:

Тогда