ВУЗы по физике
Готовые работы по физике
Как писать работы по физике
Примеры решения задач по физике
Решить задачу по физике онлайнПоле электрического диполя
так как (см. 4.1.7)
б) когда поле рассматривается с учетом самого заряда. Разложим функцию 
в трехмерный интеграл Фурье:
|
r
z |
где
|
– некоторый постоянный вектор; 
– Фурье-образ:
Для вычисления этого интеграла предположим, что 
. Тогда
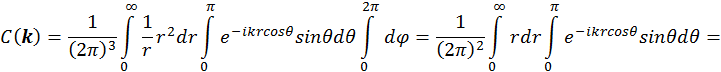
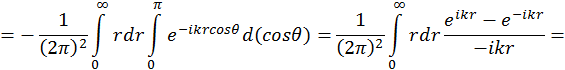
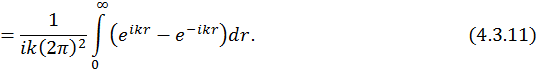
Чтобы исключить неопределенность периодических функций на бесконечности, введем число α и определим, что будет на бесконечности.
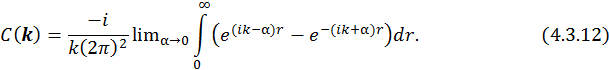
Учитывая то, что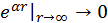 
, получим
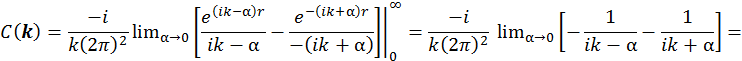
Таким образом, получаем
Тогда
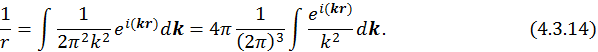
Подействуем оператором Лапласа на функцию 
:
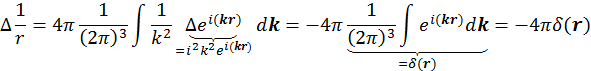
следовательно, согласно (4.3.5) и (4.3.6)
Поле электрического диполя.
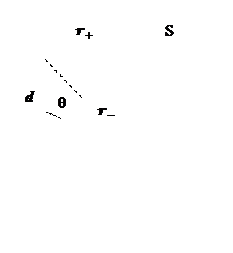
В простейшем случае электрическим диполем называется система, состоящая из двух разноименных точечных зарядов, но одинаковых по модулю и расположенных на одинаковом расстоянии друг от друга.
|
d – + |
Физической характеристикой электрического диполя является вектор
|
где 
– электрический дипольный момент.
Будем считать, что является внутренней характеристикой системы зарядов, которая не изменяется при наложении внешнего поля, т. е.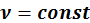 
.
Диполь называется точечным, если расстояние от диполя, на котором наблюдается его собственное поле много больше размеров диполя, т. е. 
. Условием точечного диполя является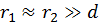 
. Между этими тремя векторами существует связь:
а т. к.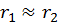 
, то 
мало.
Найдем потенциал точечного диполя. Согласно принципу суперпозиции полей:
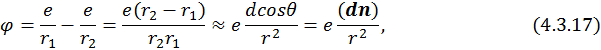
где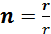 
– единичный вектор. С учетом (4.3.16) для потенциала электрического поля получим
Таким образом, поле диполя можно выразить через его дипольный момент, внутреннюю характеристику. Теперь найдем напряженность электрического поля точечного диполя.
Таким образом,
|
Введем сферическую систему координат. Вектор
следовательно,
где
|
направим по оси Z.
Найдем проекции напряженности электрического поля 
на вектора 
, 
и 
.
МГМИМО