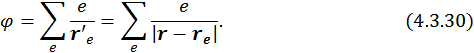Поля мультиполей

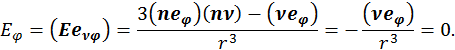
Объединяя результаты, получим вектор напряженности электрического поля, равный:

На практике мы имеем дело не с двумя, а с большим числом зарядов, образующих в данный момент ту или иную конфигурацию электрических зарядов. Тогда есть усредненное значение.

Рассмотрим случай системы зарядов.

где – мгновенное значение электрического дипольного момента. Приведем это выражение к стандартному виду. Для этого введем две точки, в которых преимущественно концентрируются положительные и отрицательные заряды

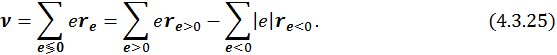
Будем считать, что система в целом нейтральна, тогда

С учетом (4.3.26) дипольный момент системы (4.3.25) можно представить в таком виде:

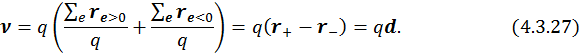
Можно показать, что если система в целом нейтральна, то определение (4.3.25) не зависит от выбора начала координат. Сдвинем начало координат на вектор , тогда:

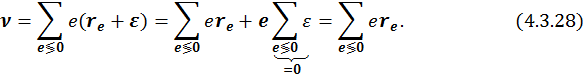
Поля мультиполей.

Идея в том, что поле сложной системы, состоящей из многих зарядов, представляется как суперпозиция полей более простых систем: кулоновское поле, поле диполя, поле квадруполя,…

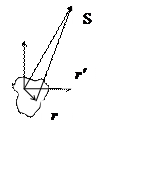
Найдем потенциал системы зарядов, совершающих заданное движение, полагая при этом, что точка наблюдения находится вдали от системы.

Т. к. , то это выражение можно разложить в ряд по малым . Сначала ограничимся двумя членами разложения:

где (производная в начале координат)

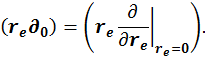
Тогда

Берем производную

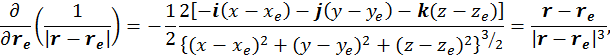
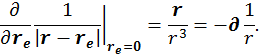
В итоге получаем, что

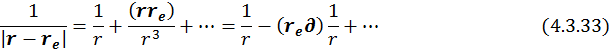
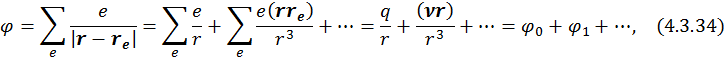
где – кулоновское поле, – поле диполя. Таким образом, мы представили поле сложной системы как сумму кулоновского, дипольного … полей. Такое разложение называется мультипольным разложением. В общем случае n – тый член разложения имеет вид:

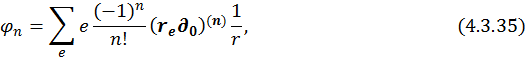
где

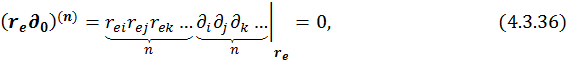
По одинаковым индексам идет суммирование ((i, j,k,…)=1,2,3

Поле квадруполя.

Глядя на формулу , можно записать

где

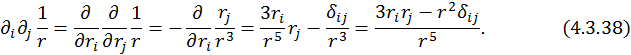
Обозначим 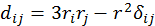– тензор второго ранга в трехмерном пространстве.

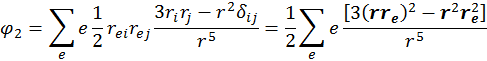
Эта формула допускает обмен индексами:

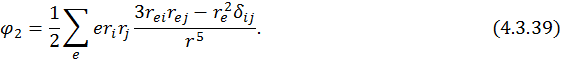
Обозначим по аналогии с электрическим дипольным моментом