Поляризация электромагнитных волн

Давление (сила Лоренца на единицу площади) равно
P=jлин B, (9)
(на поверхности металла выбираем прямоугольную площадку, определяем ток и затем силу Лоренца, действующую на этот ток, затем делим на величину площадки). Подставляя значения jпов и B из (8) и (9), найдем
P= 2eoE2=2eoEo2sin2wt. (10)
Среднее по периоду значение sin2wt равно 1/2, поэтому
<P> =eoEo2 . (11)

4. Домашнее задание

4.1 Теоретический материал

Проработать теоретический материал занятия по пособию и своему конспекту.

4.2 Решение задач

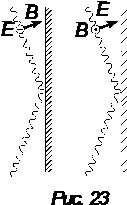Задача 1 [C12.1.25]. Пользуясь методом, изложенным в условии задачи 1, докажите, что угол отражения электромагнитной волны от металлической плоскости равен углу падения. Рассмотрите случаи:
а) вектор напряженности падающей волны параллелен металлической поверхности;
б) вектор магнитной индукции падающей волны параллелен металлической поверхности.

Задача 2 [C12.1.21]. На металлическую стенку падает перпендикулярно ее поверхности импульс электромагнитной волны, рассмотренный на занятии 1.1.3. Напряженность электрического поля импульса равна E. Определите давление волны на стенку.

ЗАНЯТИе 1.1.7

поляризация

1. Обсуждение домашнего задания

1.1 Сдать письменные ответы на вопросы домашнего задания

2. Поляризация электромагнитных волн

2.1 Виды поляризации электромагнитных волн

Плоскость, в которой лежат вектор распространения волны и вектор магнитной индукции, называется плоскостью поляризации. Если плоскость поляризации не изменяется со временем, то волна является плоскополяризованной. Далее будем говорить не о векторе магнитной индукции, а о векторе напряженности электрического поля волны.

2.1.1 Сложение плоскополяризованных волн. Разложение поляризации на составляющие

Получение электромагнитных волн различной поляризации разберем на примере решения следующей задачи.

Задача 1. Вектор напряженности электрического поля синусоидальной электромагнитной волны, распространяющейся в направлении оси OZ, колеблется в направлении оси OY. Амплитуда колебаний равна Eo. На эту волну налагается другая синусоидальная волна, распространяющаяся в том же направлении, с напряженностью электрического поля, колеблющейся с той же частотой в направлении оси OX-Ex=aEY. Сдвиг фаз равен нулю. Как ориентирована плоскость поляризации и чему равна амплитуда результирующих колебаний при: a=0; a=1; a=31/2; a=–31/2.

Решение. Идею можно пояснить чертежом с векторами напряженности волн-слагаемых. Поскольку сдвиг фаз отсутствует, соотношение между слагаемыми не изменяется со временем. Поясняющую картину лучше делать для случая a=1. На рисунке 25 показана такая картина сложения электрических векторов в четыре разные моменты времени (a=1).

При a=0 вектор электрического поля колеблется в плоскости YOZ. Амплитуда колебаний равна E0. При a=1 электрический вектор колеблется в плоскости, составляющей угол j=45о с плоскостью YOZ. Амплитуда колебаний равна . При a= tgj=, j=30о. Амплитуда колебаний равна 2E0. В последнем случае амплитуда колебаний по-прежнему равна 2E0 , а ориентация плоскости поляризации симметрична предпоследнему случаю: j=180о-30о=150о.

Из решения задачи 1 ясно, что любую плоскополяризованную волну можно представить как суперпозицию двух волн со взаимно перпендикулярными плоскостями поляризации.

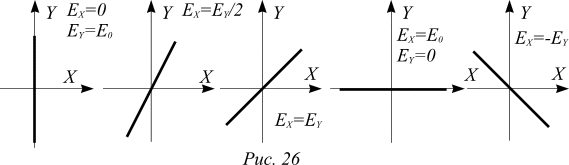На рисунке 26 показаны несколько случаев наложения волн со взаимно перпендикулярными плоскостями поляризации, в результате которого получается плоскополяризованная волна.

Задача 2. Электромагнитная волна распространяется в направлении OZ. Плоскость, в которой колеблется вектор напряженности электрического поля, составляет с плоскостью YOZ угол 30о, распределение электрического поля описывается законом E(z; t)=Eosin(kz-wt). Как распределены элект­рические поля составляющих волн по осям OX и OY?

2.1.2 Круговая и эллиптическая поляризация

Пусть в направлении оси OZ распространяются две электромагнитные волны. Напряженность электрического поля одной волны колеблется в направлении оси OY по закону EY(z, t)=Eosin(kz—wt), а другой — в направлении оси OX по закону Ex(z, t)=Eocos(kz—wt). Фаза колебаний волны с электрическим полем, ориентированным по оси OX, отстает на p/2 от фазы другой волны. Выясним характер колебаний вектора напряженности результирующей волны.

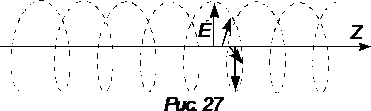Можно просто убедиться, что модуль результирующей волны со временем не изменяется и всегда равен Eo. Тангенс угла между осью OX и вектором напряженности электрического поля в точке z равен
tgj===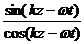tg(kz—wt). (1)

Из (1) следует, что угол между вектором напряженности электрического поля волны и осью OX — j — со временем изменяется по закону j(t)=kz—wt. Вектор напряженности электрического поля равномерно вращается с угловой скоростью, равной w. Конец вектора напряженности электрического поля движется по винтовой линии (см. рисунок 27). Если смотреть на изменение вектора напряженности из начала координат в направлении распространения волны, то вращение происходит по часовой стрелке, т. е. в направлении вектора магнитной индукции. Такую волну называют право поляризованной по кругу.

Электромагнитная волна с круговой поляризацией, падая на вещество, передает вращение электронам вещества.

Задача 3. Плоская электромагнитная волна с круговой поляризацией по часовой стрелке падает на металлическую пластинку. Напряженность электрического поля волны E0.
а) Покажите, что электроны проводимости под действием электрического поля совершают вращательное движение. Как направлено вращение?
б) Чему равен момент импульса, переданный волной электрону? Какой вывод можно сделать о наличии момента импульса у волны?

Решение. а) Полагаем, что на электроны проводимости не действует возвращающая сила (они свободны), тогда уравнения движения электрона в плоскости XOY будут иметь вид:
meax=-eEocos(kz—wt) Û ax=—cos(wt—a) (2) meay=-eEo sin(kz—wt) Û ay=+sin(wt—a). (3) Модуль ускорения постоянен и равен
a=. (4)
Из выражения для тангенса угла поворота вектора ускорения (аналогично (1)) ясно, что он вращается с постоянной угловой скоростью w. Вращение с направлением распространения волны составляют правый винт (по часовой стрелке). Отсюда следует, что электроны движутся по окружностям постоянного радиуса с угловой скоростью w. Радиус окружности можно определить из кинематического соотношения a=w2r, откуда
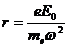(5)
Момент импульса электрона L=mevr=mewr2 с учетом уравнения (5) —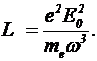
(6)
Момент импульса электрона параллелен направлению распространения волны.