Преобразования лоренца
Решение. С точки зрения наблюдателя, движущегося вместе с мюоном, со скоростью v навстречу ему несутся и атмосфера, и регистрирующие детекторы. Толщина движущейся атмосферы в 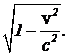 раз меньше толщины покоящейся атмосферы. Это меньшее расстояние детекторы пролетят за время
раз меньше толщины покоящейся атмосферы. Это меньшее расстояние детекторы пролетят за время 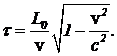
За это время число мюонов уменьшится в 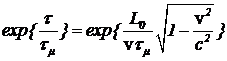 раз, что совпадает с результатом
раз, что совпадает с результатом 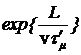 полученным с точки зрения земного наблюдателя.
полученным с точки зрения земного наблюдателя.
Задача 5. Для регистрации заряженных частиц используют устройство, называемое пузырьковой камерой. Оно устроено следующим образом. Регистрирующая камера при низкой температуре заполняется жидким водородом. Жидкость настолько тщательно очищена, что в ней нет зародышей образования пузырьков пара. Это позволяет поднять температуру водорода выше температуры кипения, не опасаясь закипания. Пролетающие с большой скоростью сквозь водород заряженные частицы ионизируют его, оставляя ионные следы. Поляризационные комки вокруг ионов становятся центрами парообразования. Водород вскипает вдоль следов. В первые мгновения кипения в камере имеются только череда пузырьков вдоль ионных следов. Их легко наблюдать визуально. Частицы, которые живут до распада ограниченный промежуток времени, оставляют отрезки пузырьковых следов — от рождения до распада. В одном из опытов при столкновении частиц высокой энергии с ядрами водорода рождались сигма-минус частицы, летящие со скоростью, отличавшейся от скорости света только на 20%. Измерения множества отрезков пузырьковых следов показали, что средняя длина следа равна 7,5 см. Как по этим данным определили собственное среднее время жизни сигма-минус частицы? Чему оно оказалось равным?
4. Домашнее задание
4.1 Теоретический материал
Проработать материал занятия по своим конспектам и по учебнику “Физика 11” под ред. А. А.Пинского. §52.
4.2 Решение задач
Задача 1[52.1]. Пи-мезоны (собственное среднее время жизни tp=2,6×10-8с) пролетают от места своего рождения до места распада в среднем 500 м. На сколько процентов их скорость отличается от скорости света?
Задача 2 [52.2]. С какой скоростью должен лететь космический корабль от Земли до далекой звезды, чтобы собственное время путешествия космонавтов было меньше (или равно) времени, необходимого свету для преодоления того же расстояния? Если свет и корабль стартуют одновременно, то свет или корабль будет первым около звезды?
Задача 3 [52.3]. Определите собственное время, необходимое для полета к астрономическим объектам: a Центавра (4 св. года); Сириусу (9 св. лет); Бетельгейзе (650 св. лет) — на космическом корабле, если его скорость составляет 0,9999999×c. При вычислениях считайте движение космического корабля на всем пути равномерным.
занятие 1.5.3
преобразования Лоренца
1.2 Контрольные вопросы
1.2.1 Поясните с помощью примера, как из постулатов теории относительности следует, что одновременные события в одной системе отсчета в другой системе могут быть неодновременными.
1.2.2 Для того чтобы в некоторой системе отсчета событию, происходящему в любой точке пространства, можно было сопоставить время, отвечающее выбранной системе отсчета, в каждую точку пространства условно надо поставить часы и синхронизировать их между собой. Предложите способ синхронизации.
1.2.3 Если часы синхронизированы в одной системе отсчета, будут ли они синхронизированными в другой? Поясните.
1.2.4 На примере действия световых часов объясните причину, почему с точки зрения “неподвижного” наблюдателя движущиеся часы идут медленнее, чем покоящиеся. Во сколько раз?
1.2.5 Как преобразуются длины при переходе из одной инерциальной системы отсчета в другую?
1.2.6 Допустим, свету на путь от Земли до звезды требуется 4 года. При скорости космического корабля, превышающей ![]() , измеренное космонавтами собственное время путешествия оказалось бы меньше 4 лет. Как такое могло бы получиться, ведь с точки зрения космонавтов, в их системе отсчета нет никакого замедления времени?
, измеренное космонавтами собственное время путешествия оказалось бы меньше 4 лет. Как такое могло бы получиться, ведь с точки зрения космонавтов, в их системе отсчета нет никакого замедления времени?
2. Преобразование координат и времени
2.1 Преобразование пространственных координат
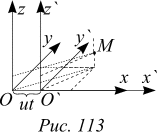 Пусть в некоторой системе отсчета в момент времени t в точке M с координатами x, y, z произошло событие. Задача состоит в том, чтобы определить координаты x`, y`, z` этой точки в новой системе отсчета, которая движется относительно исходной равномерно прямолинейно со скоростью
Пусть в некоторой системе отсчета в момент времени t в точке M с координатами x, y, z произошло событие. Задача состоит в том, чтобы определить координаты x`, y`, z` этой точки в новой системе отсчета, которая движется относительно исходной равномерно прямолинейно со скоростью ![]() . Направим координатные оси обеих систем координат так, чтобы оси OX и O`X` были параллельны направлению относительной скорости и шли вдоль одной прямой, и остальные оси были бы взаимно параллельны. Пусть начало координат штрихованной системы отсчета в момент времени t=0 совпадало с началом координат нештрихованной системы. За время t начало штрихованной системы координат сместится на ut.
. Направим координатные оси обеих систем координат так, чтобы оси OX и O`X` были параллельны направлению относительной скорости и шли вдоль одной прямой, и остальные оси были бы взаимно параллельны. Пусть начало координат штрихованной системы отсчета в момент времени t=0 совпадало с началом координат нештрихованной системы. За время t начало штрихованной системы координат сместится на ut.
С точки зрения наблюдателя, находящегося в нештрихованной системе отсчета, точка M по оси OX в момент времени t находится на расстоянии x-ut от начала координат движущейся системы отсчета. Но нам известно, что для наблюдателя в штрихованной системе отсчета отрезок x-ut преуменьшен в 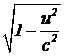 раз, поэтому, чтобы определить координату x` в штрихованной системе отсчета, надо длину отрезка x-ut увеличить в
раз, поэтому, чтобы определить координату x` в штрихованной системе отсчета, надо длину отрезка x-ut увеличить в 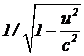 раз, т. е.
раз, т. е.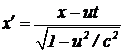 . (1) Формула (1) дает преобразование пространственной координаты x при переходе в новую инерциальную систему отсчета.
. (1) Формула (1) дает преобразование пространственной координаты x при переходе в новую инерциальную систему отсчета.
2.2 Преобразование времени
Рассмотрим предварительно вопрос о том, что значит знать координату и знать момент времени события в некоторой системе отсчета. Знание времени любого события предполагает, что в любой точке пространства можно поставить часы, которые синхронизированы с часами, установленными в начале координат. Показываемое время часами, установленными в точке x в момент события, и есть время наступления события. Синхронизированные часы тикают одновременно, или одновременно высвечивают одни и те же цифры на табло. Процесс синхронизации всех часов в какой-либо системе отсчета можно провести следующим образом. Из начала нашей системы отсчета посылается световой сигнал в точку x, где стоят часы. Эти часы устанавливаются по сообщенному сигналом времени с учетом запаздывания светового сигнала, равного x/c.
Представим, что у наблюдателя в движущейся (штрихованной) системе отсчета в момент происшествия события, о котором шла речь в разделе 2.1, часы еще не запущены. Ему надо запустить свои часы, отмеряющие время t`, так, чтобы они показывали правильное время наступления события. Причем на момент времени, когда оба начала координат совпадали, приходилась метка времени t`=0. Наблюдатель располагает информацией только о координате x и о моменте времени t данного события, измеренными в нештрихованной системе отсчета.
Наблюдатель в штрихованной системе отсчета в момент события должен взглянуть на часы нештрихованной системы координат, стоящие в точке M, которые показывают t и, учитывая, что нештрихованная система координат движется относительно него со скоростью –v и время, на его взгляд, в нашей системе отсчета течет медленнее, чем в его, должен бы установить время 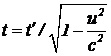 . Однако здесь он вовремя вспоминает, что синхронизированные в нештрихованной системе отсчета часы с точки зрения штрихованной системы отсчета не синхронизированы (см. ситуацию с одновременным открыванием дверей вагона электрички с точки зрения наблюдателя на платформе и неодновременным с точки зрения наблюдателя из движущегося другого поезда). Он понимает, что надо сделать поправку величины t, стоящей в числителе его выражения времени, на несинхронность. Чтобы определить эту поправку, он рассматривает наш процесс синхронизации часов со своей точки зрения. Из штрихованной системы отсчета видно, что “нештрихованные” часы движутся назад, навстречу световому сигналу. Из-за движения часов расстояние, пройденное светом, сокращается. За время достижения x/c сокращение достигает значения u(x/c). Таким образом, если раньше, в нештрихованной системе отсчета, поправка на запаздывание была равна x/c, то с точки зрения наблюдателя в штрихованной системе отсчета эта величина завышена на (ux)/c2. Таким образом, с учетом поправки на несинхронность наблюдатель должен поставить свои часы на
. Однако здесь он вовремя вспоминает, что синхронизированные в нештрихованной системе отсчета часы с точки зрения штрихованной системы отсчета не синхронизированы (см. ситуацию с одновременным открыванием дверей вагона электрички с точки зрения наблюдателя на платформе и неодновременным с точки зрения наблюдателя из движущегося другого поезда). Он понимает, что надо сделать поправку величины t, стоящей в числителе его выражения времени, на несинхронность. Чтобы определить эту поправку, он рассматривает наш процесс синхронизации часов со своей точки зрения. Из штрихованной системы отсчета видно, что “нештрихованные” часы движутся назад, навстречу световому сигналу. Из-за движения часов расстояние, пройденное светом, сокращается. За время достижения x/c сокращение достигает значения u(x/c). Таким образом, если раньше, в нештрихованной системе отсчета, поправка на запаздывание была равна x/c, то с точки зрения наблюдателя в штрихованной системе отсчета эта величина завышена на (ux)/c2. Таким образом, с учетом поправки на несинхронность наблюдатель должен поставить свои часы на
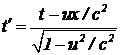 . (2)
. (2)


