Принцип гюйгенса-френеля
Явление, заключающееся в рассеянии электромагнитной волны при прохождении препятствия, сопровождающееся интерференцией рассеянных волн, называется дифракцией.
2.2 Принцип Гюйгенса-Френеля
Рассмотрим прохождение плоской электромагнитной волны через отверстие в непрозрачном экране. Определим напряженность электрического поля EA в точке A (от генератора по другую сторону экрана, там, где указан приемник на рисунке 40). Напряженность электрического поля в любой точке представляет собой сумму электрического поля электромагнитной волны, создаваемой источником Es, и электрического поля волны, излучаемой движущимися зарядами в заслонке (см. ниже) Eэ. Так что
EA=Es+Eэ. (1)
Если закрыть отверстие в экране заслонкой, изготовленной из того же материала, что и экран, то напряженность электрического поля в точке A в этом случае будет равной нулю . Заметим, что ![]() есть сумма Es+Eэ и плюс к этому электрическое поле, созданное зарядами в заслонке Eзас. Итак,
есть сумма Es+Eэ и плюс к этому электрическое поле, созданное зарядами в заслонке Eзас. Итак,
0=Es+Eэ+Eзас. (2)
Вычтем почленно из уравнения (1) уравнение (2). Тогда
EA=-Eзас. (3)
Уравнение (3) говорит, что отверстие действует как генератор, излучающий за экран.
Напряженность электрического поля —Eзас можно определить из следующих соображений. Пусть в поле E` падающей волны находится только одна заслонка. Непосредственно за заслонкой электрическое поле равно нулю. Значит, Eзас непосредственно за затычкой равно минус электрическому полю источника в том же самом месте. Для практических расчетов электрического поля волны, излучаемой пространством в отверстии, применяется следующий прием. Отверстие разбивается на малые площадки. Каждая площадка излучает, как точечный источник. Результирующее поле в точке наблюдения равно геометрической сумме вкладов от каждой бесконечно малой площадки с учетом фазы. В этом состоит принцип Гюйгенса-Френеля.
Согласно данному принципу каждая точка пространства, в которую попала волна, становится источником электромагнитной волны. Все выглядит так, как будто пространство заполнено подвижными зарядами, которые начинают колебаться под действием проходящей через них электромагнитной волны и излучать. Но при этом сама первичная волна исчезает. Волновое поле за областью, куда попала волна, заполняется только вторичными волнами.
Необычность выдвинутых Френелем представлений состоит в том, что согласно им волновое поле представляет собой интерференцию вторичных волн, рассеянных пустым пространством. Волна, распространяющаяся в пустом пространстве, при отсутствии какой либо дифракции также представляет собой наложение вторичных волн. Вторичные волны так складываются, что в результате получается невозмущенная волна.
Формулировка принципа Френеля выглядит так.
Каждая точка фронта электромагнитной волны является элементарным источником вторичных электромагнитных волн той же поляризации, что и у первичной волны, излучающих во всех направлениях. Напряженность электрического поля, переносимая элементарной вторичной волной в точку A, находящуюся на расстоянии r, задается выражением ![]() , где С — постоянная. Напряженность результирующего электрического поля в точке A является результатом интерференции вторичных волн.
, где С — постоянная. Напряженность результирующего электрического поля в точке A является результатом интерференции вторичных волн.
Явление дифракции в опыте 1 при этом представляется естественным следствием вторичного излучения. Немонотонная зависимость интенсивности электромагнитной волны за экраном с двумя щелями в опыте 2 является результатом того, что интерферируют вторичные волны от двух щелей. Аналогично объясняется расщепление светового пучка при прохождении дифракционной решетки.
2.3 Расчет дифракционной картины от двух щелей
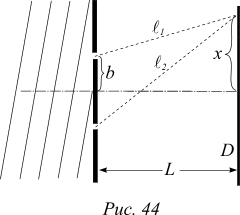
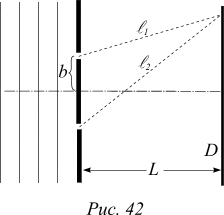 Имеем физическую ситуацию опыта 2. Положим, что источник электромагнитных волн находится очень далеко от экрана, так что на щели падает плоская электромагнитная волна. Расстояние между щелями 2b, расстояние от экрана со щелями до экрана D, на котором наблюдается дифракционная картина, — L. Пусть ширина щелей гораздо меньше длины волны l, так что вторичные волны, приходящие в точку наблюдения от разных участков щели, имеют практически одинаковые фазы.
Имеем физическую ситуацию опыта 2. Положим, что источник электромагнитных волн находится очень далеко от экрана, так что на щели падает плоская электромагнитная волна. Расстояние между щелями 2b, расстояние от экрана со щелями до экрана D, на котором наблюдается дифракционная картина, — L. Пусть ширина щелей гораздо меньше длины волны l, так что вторичные волны, приходящие в точку наблюдения от разных участков щели, имеют практически одинаковые фазы.
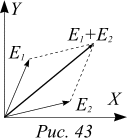
Рассчитаем распределение интенсивности электромагнитной волны на экране D как функцию расстояния x от плоскости симметрии до точки наблюдения. Так как напряженность электромагнитной волны в каждой точке представляет собой гармонические колебания, воспользуемся методом векторных диаграмм. Вклад верхней щели в напряженность электрического поля в точке x равен 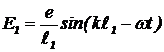 . Вклад нижней щели —
. Вклад нижней щели — 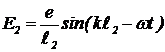 . Результирующая напряженность в точке x — E(x)= E1+E2, то есть
. Результирующая напряженность в точке x — E(x)= E1+E2, то есть 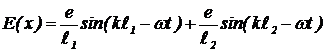 . (4)
. (4)
 И первое и второе слагаемые в уравнении (4) равны проекциям на ось ординат векторов с модулями
И первое и второе слагаемые в уравнении (4) равны проекциям на ось ординат векторов с модулями 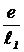 и
и ![]() , вращающимися с одинаковыми угловыми скоростями w. Их сумма равна проекции на ось ординат суммы векторов. Амплитуда колебаний напряженности электрического поля волны Eо(x) равна модулю вращающегося вектора суммы E1+Е2. По теореме косинусов, он равен
, вращающимися с одинаковыми угловыми скоростями w. Их сумма равна проекции на ось ординат суммы векторов. Амплитуда колебаний напряженности электрического поля волны Eо(x) равна модулю вращающегося вектора суммы E1+Е2. По теореме косинусов, он равен
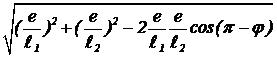 , (5)
, (5)
где j— угол между направлениями складывающихся векторов. Интенсивность волны I(x) пропорциональна квадрату амплитуды напряженности:
(6)
Угол между направлениями складывающихся векторов j равен разности фаз вкладов: ![]() . При изменении положения приемника x изменяется разность хода l2 — l1 и соответственно изменяется, проходя максимумы и минимумы, интенсивность I(x).
. При изменении положения приемника x изменяется разность хода l2 — l1 и соответственно изменяется, проходя максимумы и минимумы, интенсивность I(x).
Выразим разность фаз через отклонение x. Из чертежа находим![]() (7)
(7)
При x, b<<L эта разность приблизительно равна ![]() (8)
(8)
Условие максимума j=2pN (N — целое), что для положений xmax дает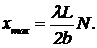 (9) Положения минимумов —
(9) Положения минимумов — 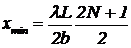 . (10)
. (10)
 Формула (6) с подстановкой вычисленной разности фаз j хорошо описывает экспериментальное распределение интенсивности.
Формула (6) с подстановкой вычисленной разности фаз j хорошо описывает экспериментальное распределение интенсивности.
Задача 1. Плоская электромагнитная волна падает на экран с двумя щелями под углом a. Расстояние между щелями равно 2b, расстояние от щелей до экрана, на котором наблюдается дифракционная картина, равно L. Найдите распределение интенсивности электромагнитной волны вдоль экрана, как функцию расстояния до оси симметрии установки x. Определите положения нулевого и первого дифракционных максимумов.
Решение. При наклонном падении электромагнитной волны на экран со щелями гребень волны вначале падает на верхнюю щель, и только через некоторое время — на нижнюю. Колебания электрического поля в щелях происходит не в фазе. Фаза колебаний в нижней щели отстает от фазы колебаний в верхней щели на d=4pb sina/l (2b sina — для волны, попадающей в верхнюю и нижнюю щели). Если вклад верхней щели в напряженность электрического поля в точке x равен 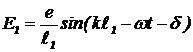 , то вклад нижней щели —
, то вклад нижней щели — 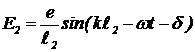 . Результирующая напряженность в точке x — E(x)= E1+ E2, т. е.
. Результирующая напряженность в точке x — E(x)= E1+ E2, т. е. 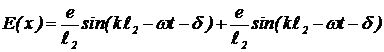 . (11)
. (11)


