Расчет балки-стенки
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
по курсу «Теория упругости и пластичности»
«РАСЧЕТ БАЛКИ-СТЕНКИ»
Задание
Схема
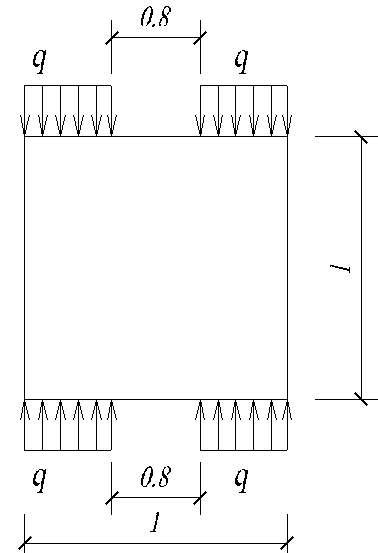
Числовые данные
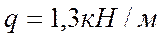
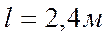
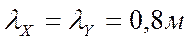
Решение
1. Образование расчетной схемы
Разбиваем сетку с шагом 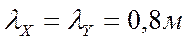 .
.
Нумерация точек приведена на рис.1.
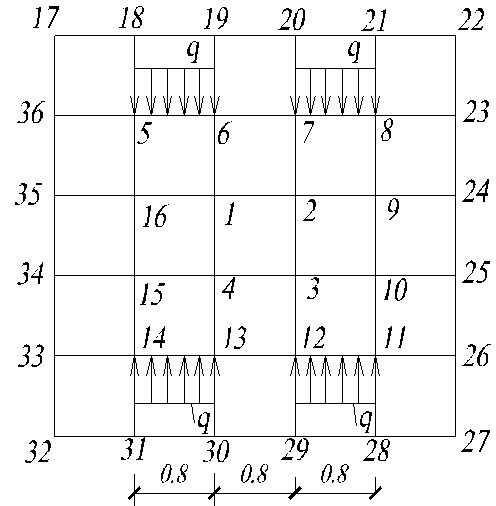
Рис.1
2. Построение эпюр M, N для заданной балки-стенки
Рассмотрим рамный аналог заданной балки-стенки (рис.2).
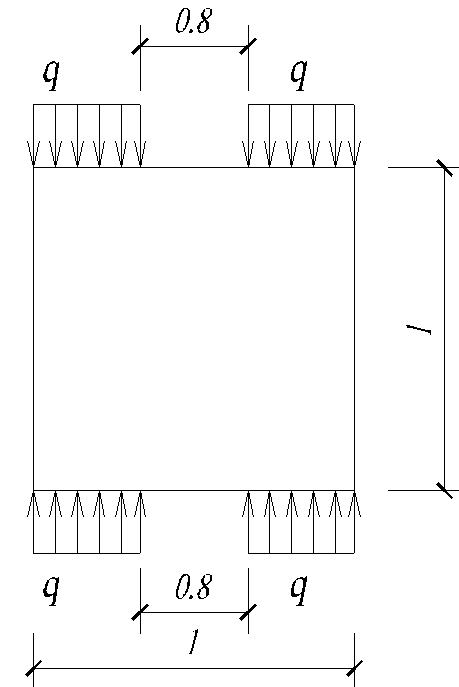
Рис.2
Участок АВ
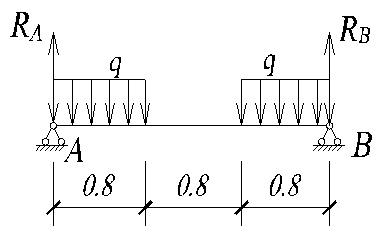 Для определения опорных реакций составим сумму моментов сил относительно точки В :
Для определения опорных реакций составим сумму моментов сил относительно точки В :
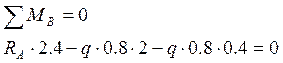
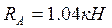
и сумму проекций действующих сил на ось y (ось y перпендикулярна оси балки)
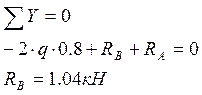
Для проверки правильности найденных опорных реакций составим сумму моментов сил относительно точки А:
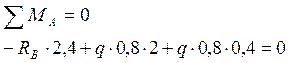
![]()
Опорные реакции найдены верно.
Составим аналитические выражения для определения внутреннего усилия в точках 5, 6, 7, 8.
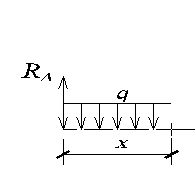
1) 0 ≤ х ≤ 0,8 м;
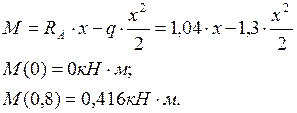
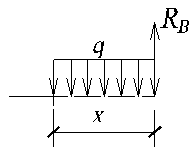
2) 0 ≤ х ≤ 0,8 м;
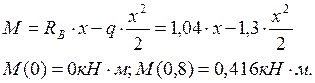
Участок СD
Расчёт участка CD ведётся аналогично. Опорные реакции, а также значения изгибающих моментов полностью совпадают с соответствующими им на участке AD, так как участки абсолютно одинаковые.
Участок СА
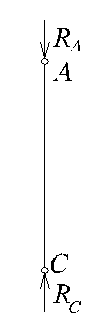 На стержень СА действуют сжимающие силы RA и RС. Используя метод сечений, можно сделать вывод, что внутреннее усилие продольная сила N постоянна по всей длине и равна
На стержень СА действуют сжимающие силы RA и RС. Используя метод сечений, можно сделать вывод, что внутреннее усилие продольная сила N постоянна по всей длине и равна
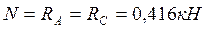 .
.
Аналогично и для участка BD.
По полученным данным построим эпюры M, N.
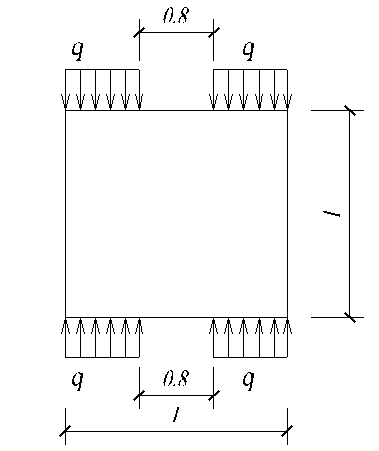
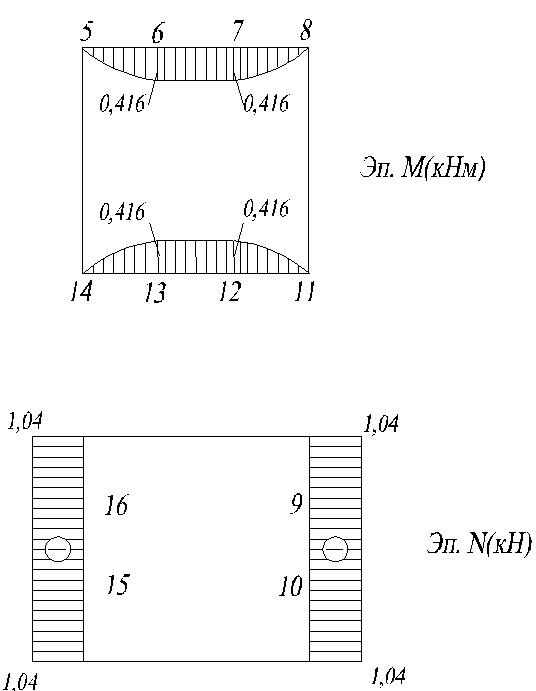
3. Определение значения функции напряжений в контурных и законтурных точках
φ5=0; φ6=0,416; φ7=0,416; φ8=0; φ9=0; φ10=0; φ11=0; φ12=0,416; φ13=0,416; φ14=0; φ15=0; φ16=0; φ18=0; φ19= φ1 + 2λ∙N6= φ1; φ20= φ2 + 2λ∙N7= φ2; φ21=0;
φ23= φ7 + 2λ∙N8= 0,416 + 2∙0,8∙(-1,04)= -1,248;
φ24= φ2 + 2λ∙N9= φ2 + 2∙0,8∙(-1,04)= φ2 -1,664;
φ25= φ3 + 2λ∙N10= φ3 + 2∙0,8∙(-1,04)= φ3 -1,664;
φ26= φ12 + 2λ∙N11= 0,416 + 2∙0,8∙(-1,04)= -1,248;
φ28= 0; φ29= φ3 + 2λ∙N12= φ3; φ30= φ4 + 2λ∙N13= φ4; φ31=0;
φ33= φ13 + 2λ∙N14= 0,416 + 2∙0,8∙(-1,04)=-1,248;
φ34= φ4 + 2λ∙N15= φ4 + 2∙0,8∙(-1,04)= φ4 -1,664;
φ35= φ1 + 2λ∙N16= φ1 + 2∙0,8∙(-1,04)= φ1-1,664;
φ36= φ6 + 2λ∙N5= 0,416 + 2∙0,8∙(-1,04)= -1,248;
4. Составление системы уравнений для нахождения значений функции напряжений во внутриконтурных точках
Предварительно запишем уравнения для каждой точки:
Точка 1
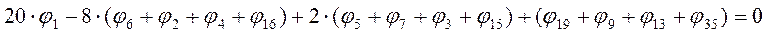
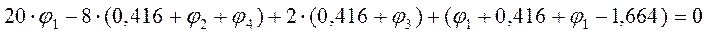
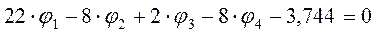
Точка 2
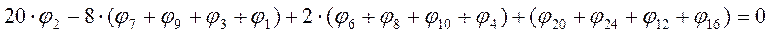
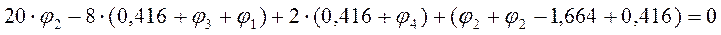
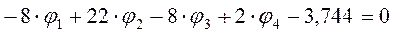
Точка3
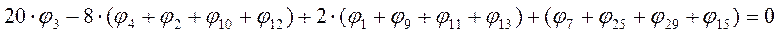
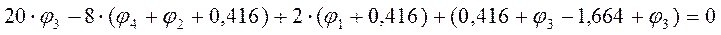
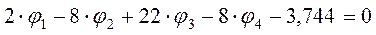
Точка4
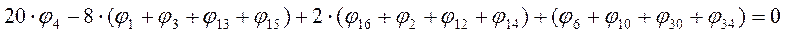
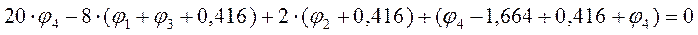
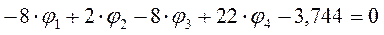
Система уравнений примет следующий вид:
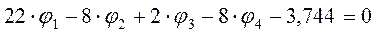
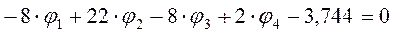
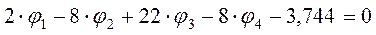
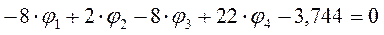
5. Решение системы уравнений
Матрица коэффициентов
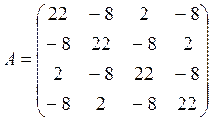
Столбец свободных членов
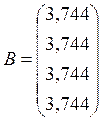
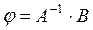
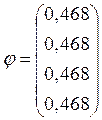
Тогда значения функции напряжений во внутриконтурных, контурных и законтурных точках будут следующими
φ1=0,468; φ2=0,468; φ3=0,468; φ4=0,468;
φ5=0; φ6=0,416; φ7=0,416; φ8=0; φ9=0; φ10=0; φ11=0; φ12=0,416; φ13=0,416; φ14=0; φ15=0; φ16=0; φ18=0; φ19=0,468; φ20=0,468; φ21=0; φ23=-1,248; φ24=-1,196; φ25=-1,196; φ26=-1,248; φ28= 0; φ29=0,468; φ30=0,468; φ31=0;
φ33=-1,248; φ34=-1,196; φ35=-1,196; φ36=-1,248;
6. Определение нормальных и касательных напряжений
Определение σX
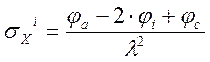
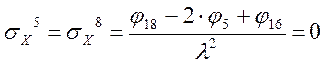
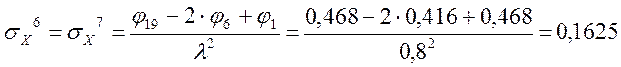
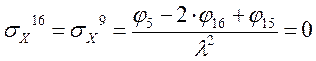
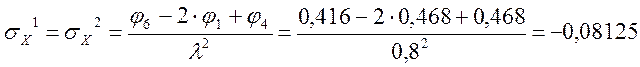
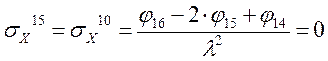
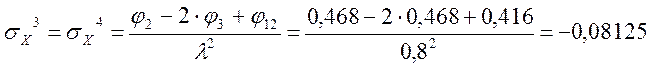
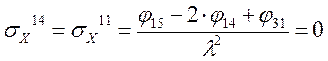
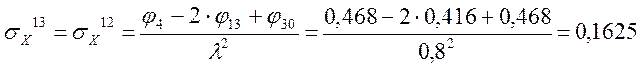
Определение σY
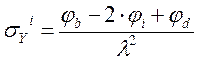
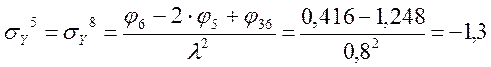
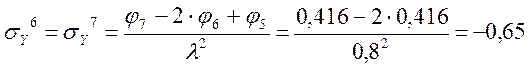
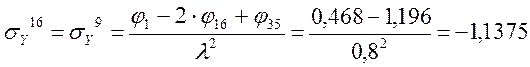
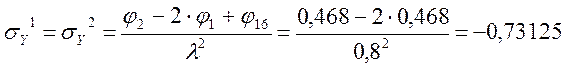
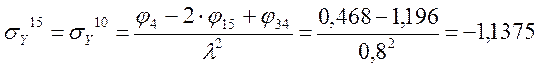
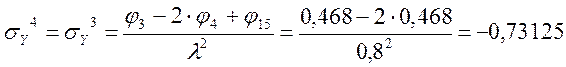
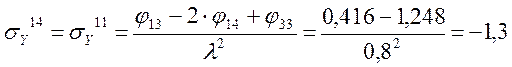
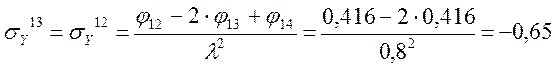
Определение τXY
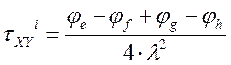
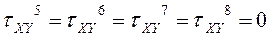
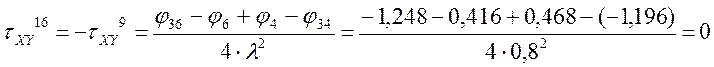
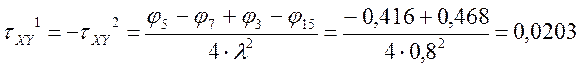
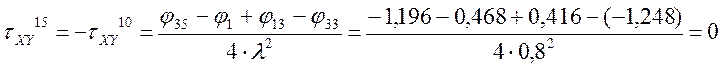
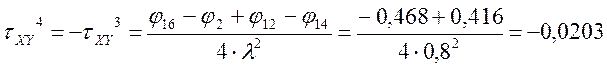
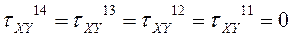
По полученным значениям строим эпюры σX, σY , τXY.
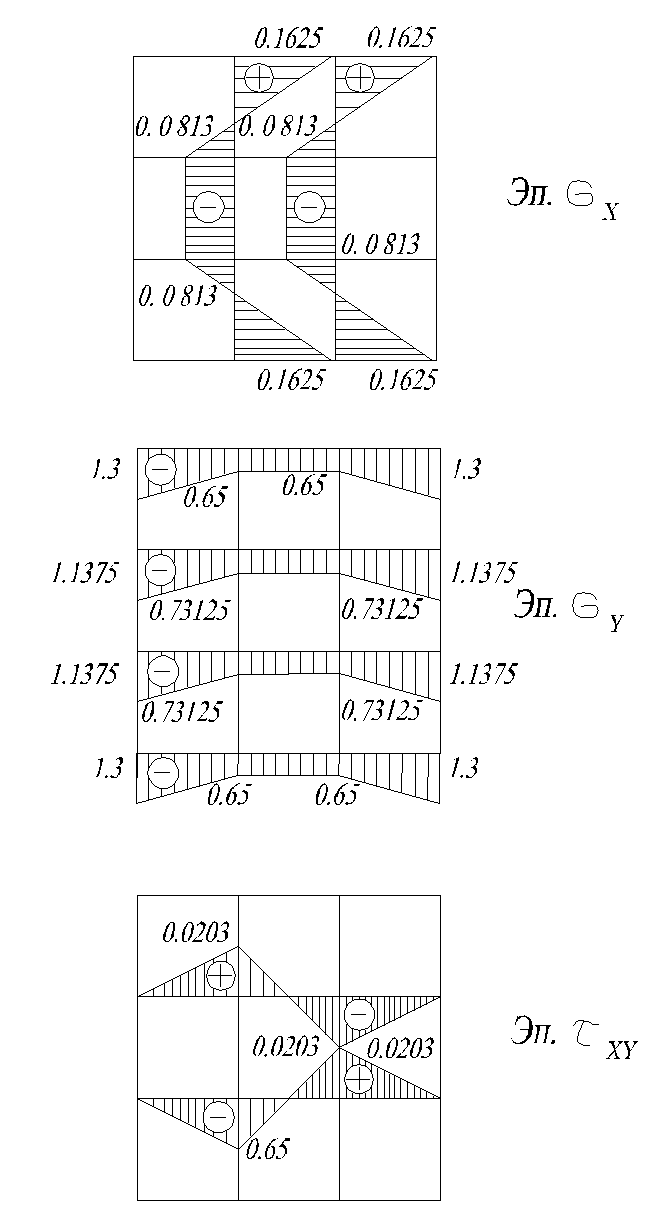
Проверка равновесия элементов балки-стенки
Составляя суммы проекций сил на оси x и y, проверим равновесие левой части балки-стенки, отсеченной по линии 6-13, и верхней части по линии 16-9 соответственно.
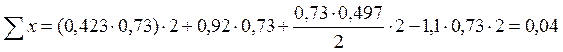
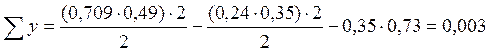
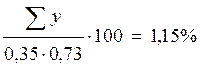
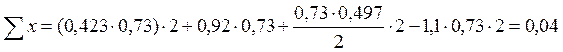
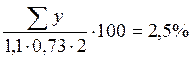
Уравнения равновесия выполняются, следовательно, решение верно.


