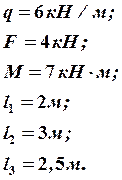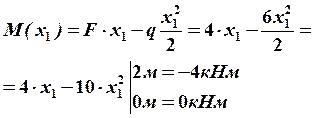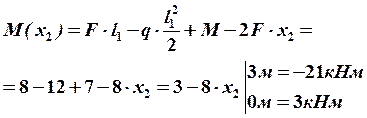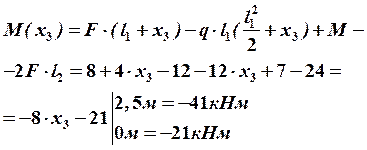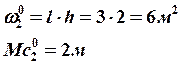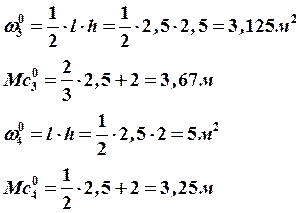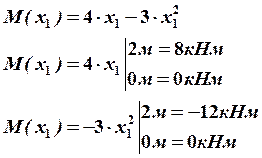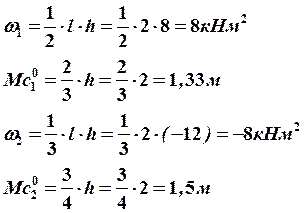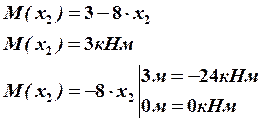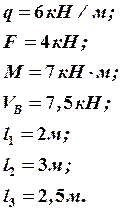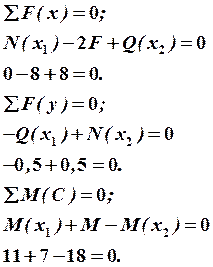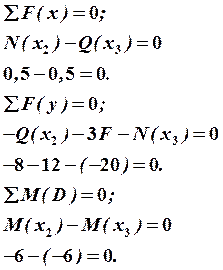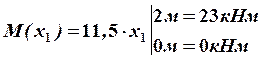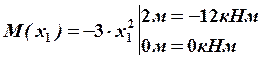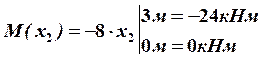ВУЗы по физике
Готовые работы по физике
Как писать работы по физике
Примеры решения задач по физике
Решить задачу по физике онлайнРасчет статически неопределимой системы
Найдем ее:
В этом сечении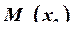 
будет иметь экстремальное значение.
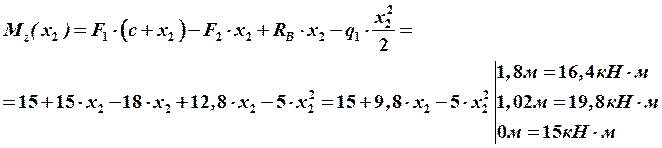
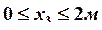
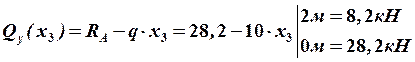
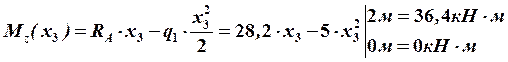
По полученным значениям строим эпюры поперечных сил 
и изгибающих моментов 
.
По условию прочности при изгибе подбираем поперечное сечение заданного профиля.
.
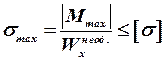Из данного выражения определяем момент сопротивления 
:
.
Для кольцевого сечения:
; .
Внешний диаметр равен:
Принимаем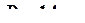 
, 
.
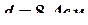Вычисляем нормальные максимальные напряжения 
и сравниваем их с допускаемыми:
.
.
.
Перегрузка не превышает 5%.
По таблицам сортимента прокатной стали (ГОСТ 8239-89) подбираем двутавр, ближайшее значение момента сопротивления .
Двутавр № 22, 
.
Определяем фактическую величину нормальных напряжений и сравниваем их с допускаемыми:
Двутавр № 22 подходит.
Расчетно-графическая работа № 2
«Расчет статически неопределимой системы»
1. Вычертим заданную схему элемента (рис. 20) с приложенными нагрузками, соблюдая масштаб длин, проставим значения размеров и нагрузок.
|
Рис. 20 Заданная схема |
Дано:
|
2. Раскрываем степень статической неопределимости.
Неизвестные реакции 
: в опоре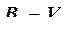 
, а в опоре 
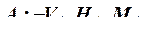, т. е. число реакций 
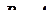. Степень статической неопределимости равна
,
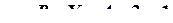где 
– число уравнений статики для плоской системы.
3. Выбираем основную (рис. 21), эквивалентную (рис. 22) системы.
|
|
|
|
Рис. 21 Основная система |
Рис. 22 Эквивалентная система и ее возможные деформациии |
Разбиваем эквивалентную систему на грузовую (рис. 23) и систему, нагруженную силой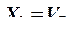 
(рис. 24).
|
|
|
|
Рис. 23 Грузовая система и ее деформации под действием внешней нагрузки |
Рис. 24 Система, нагруженная силой под действием этой нагрузки |
4. Строим единичную систему и изображаем на расчетных схемах деформацию осей всех систем и перемещения 
, 
, 
, напишем условие совместности деформаций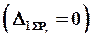 
.
Для нахождения перемещения 
(рис. 24) необходимо (в соответствии с методами Мора и Верещагина) в т. основной системы приложить силу 
по направлению неизвестной реакции 
, получим единичную систему, перемещение (деформация) которой будет равно (рис. 25).
Тогда
.
|
|
|
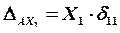Рис. 25 Единичная система |
Деформацию 
(рис. 23) обозначим как – перемещение по направлению силы 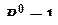от действия всей внешней нагрузки, затем подсчитываем методами Мора и Верещагина.
Используя принцип независимости действия сил, условие совместности деформаций запишем в виде:
.
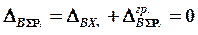5. Напишем каноническое уравнение метода сил – уравнение совместности деформаций.
Для этого, подставив значения 
и , в условие совместности деформаций, получим каноническое уравнение метода сил для одного неизвестного:
.
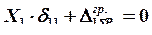6. Определим значения изгибающих моментов грузовой и единичной систем и построим эпюры.
Разбиваем грузовую и единичную системы на одинаковые силовые участки и составляем необходимые уравнения.
|
Грузовая система: |
Единичная система: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Строим эпюры изгибающих моментов от заданной нагрузки и единичной силы (рис. 26).
|
|
|
Рис. 26 Эпюры изгибающих моментов от заданной нагрузки
7. Определяем неизвестные канонического уравнения и методами Мора и Верещагина, находим неизвестную реакцию.
Принимаем жесткость всех элементов постоянной, т. е. 
.
1) Определяем перемещения 
методом Мора:
,
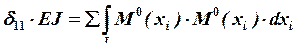где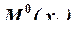 
– значение изгибающего момента на 
— том силовом участке от действия единичной силы.
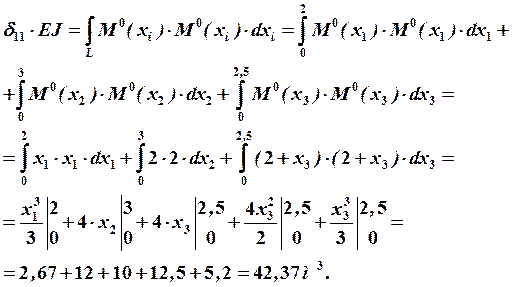
Проверка методом Верещагина:
,
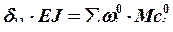где – площадь эпюры изгибающих моментов от единичной силы;
– ордината, взятая против центра тяжести эпюры изгибающих моментов от единичной силы, из той же эпюры, располагаемой под первой.
|
|
|
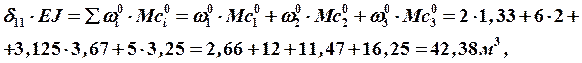
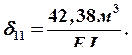
2) Определяем перемещения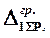 
методом Мора:
,
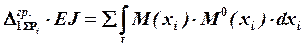где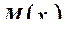 
– значение изгибающего момента на 
-том силовом участке от действия заданных сил;
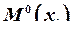– значение изгибающего момента на -том силовом участке от действия единичной силы.
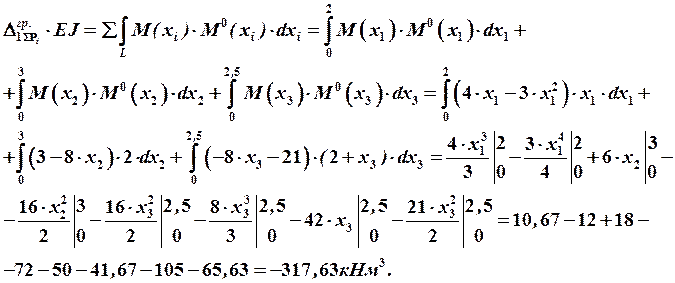
Проверка методом Верещагина:
,
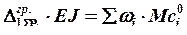где – площадь эпюры изгибающих моментов от заданных нагрузок;
– ордината эпюры изгибающих моментов от единичной силы, расположенная под центром тяжести эпюры изгибающих моментов от заданных нагрузок.
|
|
Разбиваем эпюру
|
|
|
Разбиваем эпюру
|
|
|
Разбиваем эпюру
|
на две:
на две:
на две:
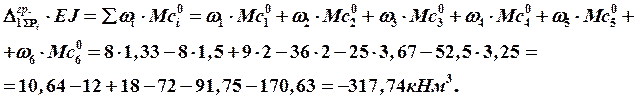
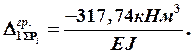
3) Определяем значение неизвестной реакции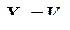 
:
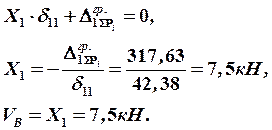
8. Вычисляем значения внутренних усилий на каждом силовом участке и строим окончательные эпюры.
|
|
Дано:
|
Рис. 27 Расчетная (эквивалентная) система
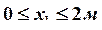
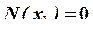
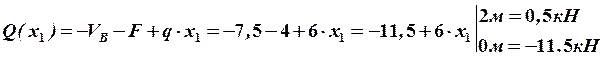
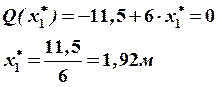
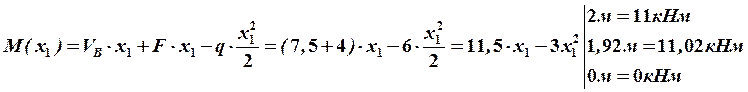
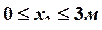
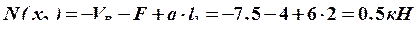
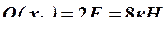
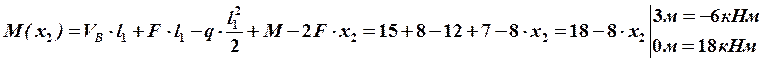
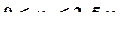
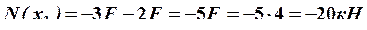
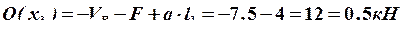
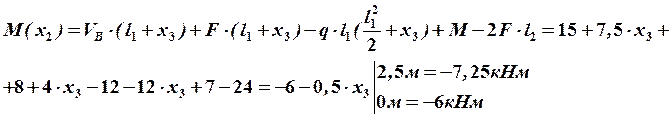
Строим окончательные (суммарные) эпюры внутренних усилий (рис. 28).
|
|
|
|
|
Рис. 28 Окончательные (суммарные) эпюры внутренних усилий |
9. Проводим статическую проверку в узлах C и D (рис. 29, 30):
|
Рис. 29 Узел С |
|
|
Рис. 30 Узел D |
|
10. Выполняем проверку равенства нулю перемещения по направлению отброшенной связи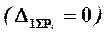 
, подтверждающую правильность определения реакции 
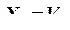, используя методы Мора и Верещагина. Она заключается в определении перемещения 
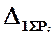в эквивалентной системе по направлению отброшенной связи с учетом найденной опорной реакции 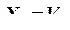, то eсть следует убедиться, что 
.
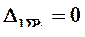Для этого используем метод Мора. Под интегралами перемножаем уравнения изгибающих моментов от суммарных внешних и единичной нагрузок на соответствующих силовых участках:
,
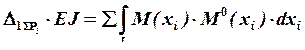где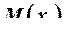 
– значение изгибающего момента на 
-том силовом участке от действия заданных внешних нагрузок и найденной реакции ;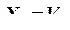
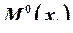– значение изгибающего момента на -том силовом участке от действия единичной силы.
|
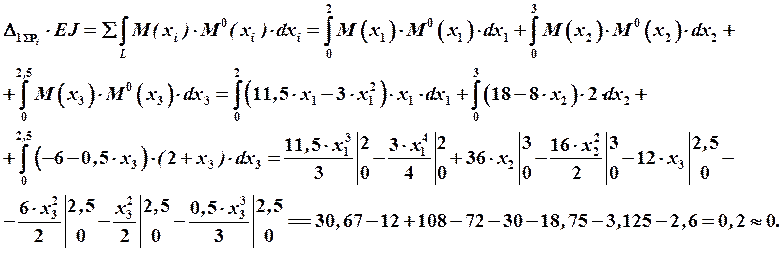
Проверка методом Верещагина:
|
Разбиваем эпюру
|
|
|
Разбиваем эпюру
|
|
|
Разбиваем эпюру
|
на две:
на две:
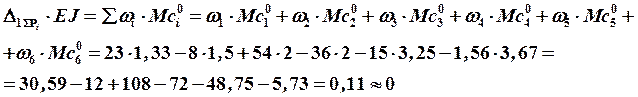
Таким образом, установлено, что реакция определена верно.
11. Подбираем поперечные сечения конструкции, состоящей из двутавровой балки и проверяем конструкцию на прочность по касательным напряжениям.
Подбор сечения осуществляется по условиям прочности при изгибе:
;
.
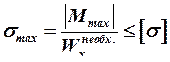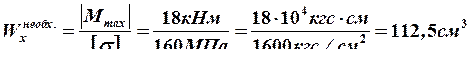Из таблицы сортамента (ГОСТ 8239 –89) выбираем двутавр № 18:
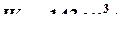
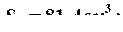
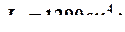
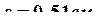
Расчет на прочность проводим по условию прочности при растяжении и изгибе:
.
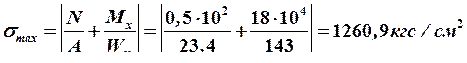Определяем перегрузку (недогрузку):
.
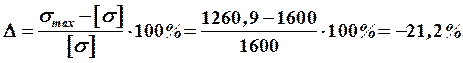Перегрузка не должна превышать + .
Проверка конструкции на прочность по касательным напряжениям осуществляется по формуле
.
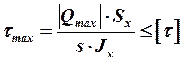Для искомой конструкции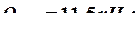 
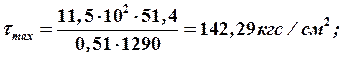
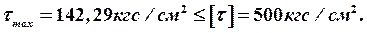
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. В чем сущность метода сквозного разреза (сечения)?
2. Какой вид нагружения называется растяжением (сжатием)?
3. Какое правило знаков принято для продольной силы? Как вычисляется значение продольной силы в поперечном сечении бруса?
4. Что называется эпюрой? Правило построения эпюры продольных сил.
5. Как вычисляются нормальные напряжения в поперечном сечении растянутого стержня?
6. Что называется абсолютным и относительным удлинением?
7. Что характеризует модуль упругости? Как он влияет на деформации бруса?
8. Что называется коэффициентом Пуассона и каковы его имеет значения?
9. Сформулируйте закон Гука.
10. Какой вид нагружения называется кручением?
11. Как определяются напряжения при кручении?
12. Что такое момент сопротивления сечения при кручении?
13. В чем состоят условия прочности при кручении?
14. Какая величина называется жесткостью при кручении?
15. Как в общем случае определяются углы закручивания?
16. Что называется чистым изгибом, поперечным изгибом?
17. Какие уравнения используются для определения опорных реакций?
18. Какие внутренние усилия возникают в поперечных сечениях бруса при изгибе?
19. Какие правила знаков приняты для каждого из внутренних усилий?
20. Чему равен изгибающий момент и поперечная сила 
в любом сечении балки?
21. Какая дифференциальная зависимость существует между поперечной силой и интенсивностью распределённой нагрузки?
22. Как определяется экстремальное значение изгибающего момента?
23. По какой формуле определяются нормальные напряжения в поперечных сечениях при изгибе?
24. Как определяются осевые моменты сопротивления прямоугольного и круглого поперечного сечения?
25. Проанализируйте формулу Журавского.
26. Что называется статически неопределимой системой?
27. Какая система называется геометрически неизменяемой?
28. В чем заключается выбор основной системы?
29. Каков физический смысл уравнений деформаций (канонических уравнений метода сил)?
30. Что означают величины 
, 
, и 
?
31. Объясните сущность метода Мора.
32. Объясните сущность метода Верещагина.
33. Как проводится статическая проверка окончательных эпюр 
, 
, 
?
34. На чем основана и как проводится деформационная проверка окончательной эпюры изгибающих моментов?
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Пирогов, Е. Н. Сопротивление материалов. С примерами типичных
расчетов [Текст] : конспект лекций / Е. Н. Пирогов.–
М. : Айрис Пресс, 2003. – 176 с.
2. Сопротивление материалов [Текст] : учеб. пособие /
под ред. Н. А. Костенко – 2-е изд., испр. – M. : Высш. шк., 2004. – 430 с.
3. Тимошенко, С. П. Механика материалов [Текст] : учеб./
С. П. Тимошенко.– СПб. : Лань, 2002. – 672 с.
4. Харчевников, В. И. Сопротивление материалов и прикладная механика [Текст] : тексты лекций / В. И. Харчевников, Т. Н. Стородубцева. – Воронеж, ВГЛТА, 2004. – 107 с.
ПРИЛОЖЕНИЯ
Площади и координаты центра тяжести простых фигур
|
Виды эпюр изгибающих моментов |
Площадь эпюры
|
Абсциссы центра тяжести эпюры |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Двутавры стальные горячекатаные (по ГОСТ 8239-89)
|
|
h – высота двутавра; b – ширина полки; s – толщина стенки; t – средняя толщина полки; A – площадь поперечного сечения; J – момент инерции; W – момент сопротивления; S – статический момент полусечения; i– радиус инерции. |
|
|
|
№ |
Размеры, мм |
, см2 |
см4 |
см3 |
, см |
, см3 |
, см4 |
, см3 |
, см |
|||
|
h |
b |
s |
t |
|||||||||
|
10 |
100 |
55 |
4,5 |
7,2 |
12 |
198 |
39,7 |
4,06 |
23 |
17,9 |
6,49 |
1,22 |
|
12 |
120 |
64 |
4,8 |
7,3 |
14,7 |
350 |
58,4 |
4,88 |
33,7 |
27,9 |
8,72 |
1,38 |
|
14 |
140 |
73 |
4,9 |
7,5 |
17,4 |
572 |
81,7 |
5,73 |
46,8 |
41,9 |
11,5 |
1,55 |
|
16 |
160 |
81 |
5 |
7,8 |
20,2 |
873 |
109 |
6,57 |
62,3 |
58,6 |
14,5 |
1,7 |
|
18 |
180 |
90 |
5,1 |
8,1 |
23,4 |
1290 |
143 |
7,42 |
81,4 |
82,6 |
18,4 |
1,88 |
|
20 |
200 |
100 |
5,2 |
8,4 |
26,8 |
1840 |
184 |
8,28 |
104 |
115 |
23,1 |
2,07 |
|
22 |
220 |
110 |
5,4 |
8,7 |
30,6 |
2550 |
232 |
9,13 |
131 |
157 |
28,6 |
2,27 |
|
24 |
240 |
115 |
5,6 |
9,5 |
34,8 |
3460 |
289 |
9,97 |
163 |
198 |
34,5 |
2,37 |
|
27 |
270 |
125 |
6 |
9,8 |
40,2 |
5010 |
371 |
11,2 |
210 |
260 |
41,5 |
2,54 |
|
30 |
300 |
135 |
6,5 |
10,2 |
46,5 |
7080 |
472 |
12,3 |
268 |
337 |
49,9 |
2,69 |
|
33 |
330 |
140 |
7 |
11,2 |
53,8 |
9840 |
597 |
13,5 |
339 |
419 |
59,9 |
2,79 |
|
36 |
360 |
145 |
7,5 |
12,3 |
61,9 |
13380 |
743 |
14,7 |
423 |
516 |
71,1 |
2,89 |
|
40 |
400 |
155 |
8,3 |
13 |
72,6 |
19,62 |
953 |
16,2 |
545 |
667 |
86,1 |
3,03 |
|
45 |
450 |
160 |
9 |
14,2 |
84,7 |
27696 |
1231 |
18,1 |
708 |
8087 |
101 |
3,09 |
|
50 |
500 |
170 |
10 |
15,2 |
100 |
39727 |
1589 |
19,9 |
919 |
1043 |
123 |
3,23 |
|
55 |
550 |
180 |
11 |
16,5 |
118 |
55962 |
2035 |
21,8 |
1181 |
1356 |
151 |
3,39 |
|
60 |
600 |
190 |
12 |
17,8 |
138 |
76806 |
2560 |
23,6 |
1491 |
1725 |
182 |
3,54 |
,
,Швеллеры стальные горячекатаные (по ГОСТ 8240-89)
|
|
h – высота швеллера; b – ширина полки; s – толщина стенки; t – средняя толщина полки; A – площадь поперечного сечения; J – момент инерции; |
W – момент сопротивления; S – статический момент полусечения; i – радиус инерции; z0 – расстояние от оси y до наружной грани стенки. |
|
№ |
Размеры, мм |
, см2 |
см4 |
см3 |
см |
см3 |
см4 |
см3 |
см |
см |
|||
|
h |
b |
s |
t |
||||||||||
|
5 |
50 |
32 |
4,4 |
7 |
6,16 |
22,8 |
9,1 |
1,92 |
5,59 |
5,61 |
2,75 |
0,95 |
1,16 |
|
6,5 |
65 |
36 |
4,4 |
7,2 |
7,51 |
48,6 |
15 |
2,54 |
9 |
8,7 |
3,68 |
1,08 |
1,24 |
|
8 |
80 |
40 |
4,5 |
7,4 |
8,98 |
89,4 |
22,4 |
3,16 |
13,3 |
12,8 |
4,75 |
1,19 |
1,31 |
|
10 |
100 |
46 |
4,5 |
7,6 |
10,9 |
174 |
34,8 |
3,99 |
20,4 |
20,4 |
6,46 |
1,37 |
1,44 |
|
12 |
120 |
52 |
4,8 |
7,8 |
13,3 |
304 |
50,6 |
4,78 |
29,6 |
31,2 |
8,52 |
1,53 |
1,54 |
|
14 |
140 |
58 |
4,9 |
8,1 |
15,6 |
491 |
70,2 |
5,6 |
40,8 |
45,4 |
11 |
1,7 |
1,67 |
|
16 |
160 |
64 |
5 |
8,4 |
18,1 |
747 |
93,4 |
6,42 |
54,1 |
63,3 |
13,8 |
1,87 |
1,8 |
|
16а |
160 |
68 |
5 |
9 |
19,5 |
823 |
103 |
6,49 |
59,4 |
78,8 |
16,4 |
2,01 |
2 |
|
18 |
180 |
70 |
5,1 |
8,7 |
20,7 |
1090 |
121 |
7,24 |
69,8 |
86 |
17 |
2,04 |
1,94 |
|
18а |
180 |
74 |
5,1 |
9,3 |
22,2 |
1190 |
132 |
7,32 |
76,1 |
105 |
20 |
2,18 |
2,13 |
|
20 |
200 |
76 |
5,2 |
9 |
23,4 |
1520 |
152 |
8,07 |
87,8 |
113 |
20,5 |
2,2 |
2,07 |
|
22 |
220 |
82 |
5,4 |
9,5 |
26,7 |
2110 |
192 |
8,89 |
110 |
151 |
25,1 |
2,37 |
2,21 |
|
24 |
240 |
90 |
5,6 |
10 |
30,6 |
2900 |
242 |
9,73 |
139 |
208 |
31,6 |
2,6 |
2,42 |
|
27 |
270 |
95 |
6 |
10,5 |
35,2 |
4160 |
308 |
10,9 |
178 |
262 |
37,3 |
2,73 |
2,47 |
|
30 |
300 |
100 |
6,5 |
11 |
40,5 |
5810 |
387 |
12 |
224 |
327 |
43,6 |
2,84 |
2,52 |
|
33 |
330 |
105 |
7 |
11,7 |
46,5 |
7980 |
484 |
13,1 |
281 |
410 |
51,8 |
2,97 |
2,59 |
|
36 |
360 |
110 |
7,5 |
12,6 |
53,4 |
10820 |
601 |
14,2 |
350 |
513 |
61,7 |
3,1 |
2,68 |
|
40 |
400 |
115 |
8 |
13,5 |
61,5 |
15220 |
761 |
15,7 |
444 |
642 |
73,4 |
3,23 |
2,75 |
,
,
,
,
,
,СОДЕРЖАНИЕ
Введение 3
Используемые обозначения и единицы измерения 4
Общие указания по выбору варианта и выполнению
расчетно-графических работ 5
Основные понятия и зависимости 6
1 Задачи курса “Сопротивление материалов” 6
2 Внутренние усилия. Метод
сквозного разреза. Типы деформации 7
3 Растяжение-сжатие 9
4 Кручение 11
5 Поперечный изгиб 14
6 Расчет на жесткость при изгибе 20
7 Статически неопределимая система 25
Темы и варианты заданий 29
Расчетно-графическая работа № 1 29
Задание 1 Осевое растяжение (сжатие) стержня 29
Задание 2 Кручение стержня круглого поперечного сечения 31
Задание 3 Расчет на прочность при изгибе 33
Расчетно-графическая работа № 2 35
Примеры решения типовых задач 38
Расчетно-графическая работа № 1 38
Задание 1 Осевое растяжение (сжатие) стержня 38
МГМИМО
Скидка 30% по промокоду Diplom2020
Получи промокод на скидку 20%
Дипломные