Распределение энергии равновесного излучения по частотам
При низких температурах 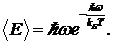 (13)
(13)
— средняя энергия электромагнитной волны стремится к нулю (к энергии основного состояния). Излучения данной частоты w в ящике не должно быть. Этот вывод не согласуется с выводами классического рассмотрения.
2.3 Распределение энергии равновесного излучения по частотам
Определим, какая энергия в тепловом равновесии газа приходится на излучение с частотой w, находящегося в ящике с зеркальными стенками. Для этого нам надо знать среднюю энергию áEñ моды электромагнитной волны с частотой w и число мод dQ, приходящееся на интервал частот от w до w+dw. Среднюю энергию и число мод надо перемножить, тогда получим среднюю энергию равновесного излучения, приходящегося на указанный выше интервал частот.
Для экономии времени и сил мы не будем выводить выражение для числа мод, а сразу воспользуемся готовым ответом.
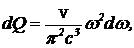 (14)
(14)
где V — объем ящика, c — скорость света. Эту формулу в свое время получили Рэлей и Джинс. Применение ее к классическому рассмотрению давало 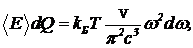 (15)
(15)
— чем выше частота излучения, тем большая энергия приходится на него. Из такого рассмотрения на кинетическую энергию движения молекул ничего не должно оставаться. Это обстоятельство П. Эренфест назвал “ультрафиолетовой катастрофой”. Но мы теперь знаем, что средняя энергия моды не равна kБT. В левую часть (15) надо подставлять правильную формулу (10) для средней энергии осциллятора. Таким образом, средняя энергия равновесного излучения dE, приходящаяся на интервал частот от w до w+dw и на единицу объема равна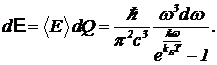 (16)
(16)
Если в стенке ящика сделать маленькое отверстие и регистрировать мощность выходящего излучения с данной частотой w, то эта мощность будет равна I(w)dw=cdE 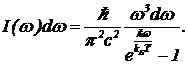 (17) Величина I(w) и есть спектральная плотность излучения. График зависимости I(w) приведен на рисунке 29. Он описывает распределение яркости в спектре равновесного излучения.
(17) Величина I(w) и есть спектральная плотность излучения. График зависимости I(w) приведен на рисунке 29. Он описывает распределение яркости в спектре равновесного излучения.
Зависимость I(w) имеет ряд замечательных свойств. Во-первых, распределение не зависит от рода излучающего газа, больше того, совершенно не существенно, газ или твердое тело дает это излучение. Оно универсально.
Зависимость I(w) обладает следующим его свойством: распределение имеет максимум. Его положение определится из уравнения ![]() . Это уравнение после преобразований принимает вид
. Это уравнение после преобразований принимает вид 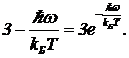 (18)
(18)
Это уравнение имеет два корня (относительно величины ![]() ). Один находится в начале координат
). Один находится в начале координат 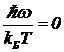 . Другой корень является тем решением, которое мы ищем. Он находится численными методами. Получается
. Другой корень является тем решением, которое мы ищем. Он находится численными методами. Получается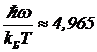 . (19)
. (19)
Так что
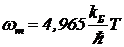 . (20)
. (20)
Данное свойство используется для измерения высоких температур.
При 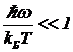 распределение дает классический закон (15). Классическая теория правильно описывает распределение спектральной плотности только в области низких частот.
распределение дает классический закон (15). Классическая теория правильно описывает распределение спектральной плотности только в области низких частот.
Используя выражение (17), можно получить полную интенсивность излучения, просуммированную по всем значениям частот 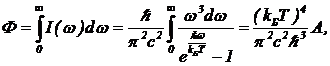 (21)
(21)
где A — число, равное ![]() , которое находится так:
, которое находится так: 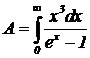 . Выражение (21) говорит, что полная яркость равновесного излучения пропорциональна четвертой степени абсолютной температуры. Зависимость полной интенсивности излучения от абсолютной температуры (21) называется законом Стефана-Больцмана. Постоянную
. Выражение (21) говорит, что полная яркость равновесного излучения пропорциональна четвертой степени абсолютной температуры. Зависимость полной интенсивности излучения от абсолютной температуры (21) называется законом Стефана-Больцмана. Постоянную 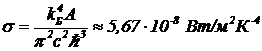 (22) называют постоянной Стефана-Больцмана.
(22) называют постоянной Стефана-Больцмана.
Закон распределения интенсивности равновесного излучения в расчете на единичный интервал частот можно записать также для величины энергии в единице объема u(w). С интенсивностью I(w) она связана соотношением I(w)=с u(w). Так же и закон Стефана-Больцмана можно записать для энергии в единице объема U(T): F=c×U(T). При этом полная энергия E равновесного излучения в ящике может быть записана так:
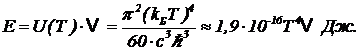 (23)
(23)
2.4 Итоги
Квантовый расчет показал, что катастрофического распределения энергии по электромагнитным модам не происходит. Возбужденными оказываются далеко не все, а Из=за этого на излучение приходится только некоторая часть тепловой энергии. При температурах, с которыми мы имеем дело в быту, большая часть полной тепловой энергии приходится на кинетическую энергию движения молекул, и только небольшая часть приходится на излучение.
Пример. В ящике объемом 1 л при температуре 300 К и атмосферном давлении находится гелий. Его раскалили до 1000 К. Чему равна кинетическая энергия движения молекул и чему равна полная энергия равновесного излучения?
Решение. При нагревании давление увеличится до 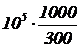 . Энергия теплового движения молекул равна
. Энергия теплового движения молекул равна ![]() Энергия излучения
Энергия излучения 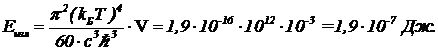 Как видно, при температуре 1000 К подавляющая часть тепловой энергии газа — это кинетическая энергия молекул, а не энергия излучения. Электромагнитное “трение” при этой температуре играет малую роль в распределении энергии.
Как видно, при температуре 1000 К подавляющая часть тепловой энергии газа — это кинетическая энергия молекул, а не энергия излучения. Электромагнитное “трение” при этой температуре играет малую роль в распределении энергии.
Тепловая энергия, приходящаяся на излучение, является степенной функцией температуры с показателем степени 4, в то время как тепловая энергия движения молекул зависит от температуры лишь линейно. Это обстоятельство существенно сказывается при высоких температурах. Так при температуре газа в миллион градусов энергия, приходящаяся на излучение, имеет тот же порядок, что и полная кинетическая энергия молекул.
Распределение энергии излучения по частотам, описываемое выражением (17), прекрасно согласуется с опытными данными. Отсюда можно сделать вывод, что идеи, положенные в основание теории равновесного излучения не противоречат эксперименту.
2.5 Решение задач
Задача 1. При какой температуре вероятность электромагнитной волне с частотой w=5×1014 Гц быть в первом возбужденном состоянии меньше вероятности быть в основном состоянии в два раза? (ln2»0,693).
Решение. Отношение вероятностей системе, находящейся в состоянии равновесия, иметь энергию E1 (энергия основного состояния) и E2 (энергия первого возбужденного состояния) равна 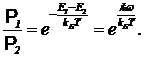 (24)
(24)
По условию 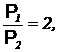 поэтому из (24) получаем
поэтому из (24) получаем 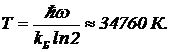 (25)
(25)
Данная в условии частота соответствует желтому свету. Результат решения говорит, что даже при высокой температуре заполненность первого уровня для желтых фотонов меньше заполненности основного уровня в два раза.
Задача 2. Астрофизики обнаружили фоновое излучение, существующее не только в галактике, но и во внегалактическом пространстве, о котором предполагают, что это остаточное излучение (реликтовое излучение) после великого взрыва, в результате которого возникла вселенная. Это излучение изотропно и распределено по частотам, как тепловое излучение тела, имеющего температуру 3 К. К какой части шкалы электромагнитных волн относится максимум интенсивности реликтового излучения?
Задача 3. Чему равна средняя энергия электромагнитной волны излучения пламени (T=1000 К) с частотой, приходящейся на максимум спектральной плотности?


