квазимонохроматическое излучение

Реальное электромагнитное излучение всегда представляет собой суперпозицию монохроматических волн с длинами волн, лежащими в некотором интервале , где — максимальная и — минимальная длина волны для данной суперпозиции. Если 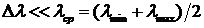, излучение называется квазимонохроматическим.

Ширина спектрального интервала влияет на наблюдаемую интерференционную картину. Интерференционные полосы, формируемые отдельными волнами с разной длиной волны, сдвинуты относительно друг друга в плоскости наблюдения. Исключением является центральная светлая полоса нулевого порядка (), для которой разность хода для всех волн равна нулю.

Сдвиг интерференционных полос пропорционален разности длин волн и растет с увеличением порядка m интерференционной полосы. Очевидно, что существует такой порядок , для которого светлая полоса для волны с в первый раз совпадает с темной полосой для волны с

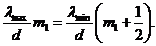(4.26)

Данное соотношение записано для опыта Юнга.

Отсюда следует, что видность интерференционной картины можно считать практически равной нулю для области интерференционных полос с

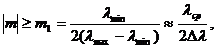(4.27)

где . Таким образом, с помощью квазимонохроматического света можно наблюдать интерференционную картину, где полное число светлых и темных полос

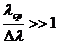, . (4.28)

В классическом опыте по наблюдению колец Ньютона величина в формуле (4.28) равна ширине полосы пропускания светофильтра.

Явление интерференции характерно для волн любой физической природы, подчиняющихся принципу суперпозиции, включая волновые поля, описывающие движение частиц в квантовой механике. Интерференция наиболее наглядно демонстрирует специфику волновых процессов, происходящих в линейных системах, и отличие волнового движения материи от её механического движения. Допустим, что в опыте Юнга на экран со щелями нормально падает однородный в поперечном сечении пучок частиц, то прошедшие через щели частицы попадают только в те области экрана наблюдения, которые являются проекциями щелей. В пределах этих областей распределение частиц равномерное без каких-либо максимумов и минимумов.

Лекция №5

Интерференция сферических монохроматических волн

1. Сферические акустические волны.

2. Интерференция скалярных сферических монохроматических волн от двух независимых источников.

3.Формирование диаграммы направленности системы когерентных источников.

4. Голография.

В этом разделе рассматривается интерференция скалярных монохроматических волн, примером которых являются акустические волны, переносящие механические колебания макроскопических элементов среды. Источником акустических волн может служить любое тело, колеблющееся в некоторой среде. В дальней зоне акустическую волну излучаемую телом конечных размеров можно всегда с необходимой точностью считать сферической. При этом центр сферических волновых поверхностей совпадает с точкой нахождения колеблющегося тела.

Допустим, что в некоторой сплошной среде пульсирует сферическое тело, радиус r которого меняется со временем по гармоническому закону

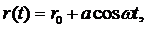(5.1)

где r0>0 и a>0 – постоянные, a<<r0, ω – частота колебаний сферической поверхности. Такое пульсирующее тело является источником сферической акустической волны с частотой ω, распространяющейся от этого тела. Если радиус r0 пульсирующего тела много меньше длины волны излучения λ, то такой излучатель в акустике называется монополем.

В дальней волновой зоне все характеристики сферической волны (смещение элементов среды, давление, изменение плотности среды) описываются с помощью функции

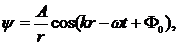(5.2)

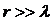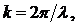
где r — расстояние от монополя до точки наблюдения, , 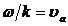— фазовая скорость акустической волны, Ф0 — начальная фаза. Если волновая функция ψ описывает смещение элементов среды вдоль радиус-вектора , то постоянная А, определяемая с помощью граничных условий на поверхности раздела тела пульсирующей среды, имеет вид

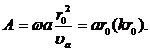(5.3)

При заданной амплитуде a колебаний поверхности монополя средняя мощность излучения монополя

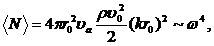(5.4)

где — амплитуда скорости сферической поверхности монополя и 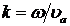. Согласно выражению (5.4) средняя мощность излучения монополя прямо пропорциональна частоте его колебаний и радиусу в четвёртой степени, т. е. очень быстро уменьшается с уменьшением частоты и ω радиуса r0.

Давление р, создаваемое сферической акустической волной в дальней зоне, описывается такой же формулой, как в случае плоской монохроматической волны:

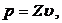(5.5)

где 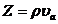— удельный акустический импеданс среды, ρ — плотность невозмущённой среды и 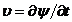— проекция вектора скорости смещения элементов среды на направление радиус-вектора , проведенного от монополя в точку наблюдения.

Пусть в среде имеются два независимых источника S1 и S2 скалярных сферических монохроматических волн ψ1 и ψ2 (рис.5.1). Расстояние между источниками равно d. Ось х проведём через источники волн, а ось z — через середину отрезка прямой, соединяющего источники. Точка наблюдения Р находится в дальней волновой зоне источников и задаётся с помощью угла θ. Осью симметрии волнового поля является ось x, поскольку пространственное распределение этого поля не зависит от поворота вокруг данной оси на произвольный угол 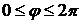.