ВУЗы по физике
Готовые работы по физике
Как писать работы по физике
Примеры решения задач по физике
Решить задачу по физике онлайнСиловой расчет
Fи = —m×as,
Mи = — Is×e,
где m – масса звена, кг;
as – ускорение центра масс звена, м/с2;
Is – момент инерции звена относительно оси, проходящей че-
рез его центр масс перпендикулярно к плоскости движения, кг×м2;
e — угловое ускорение звена, с-2.
Методы динамического анализа (исследования) в данном курсе рассматриваются применительно к плоским механизмам с одной степенью свободы, которые являются наиболее распространенными. Одной из задач динамического анализа механизма является проведение кинетостатического (силового) расчета, при котором определяются реакции в кинематических парах и уравновешивающий момент (уравновешивающая сила), приложенный к исходному механизму от действия внешних сил и сил инерции.
Силовой расчет ведется с использованием принципа д’Аламбера методом планов сил по отдельным структурным группам Ассура, представляющих собой кинетостатически определимые системы (кинематические цепи). Для этих цепей число неизвестных реакций в кинематических парах равно числу условий кинетостатики. Знание реакций в кинематических парах необходимо для расчета звеньев механизма на прочность. Уравновешивающий момент обеспечивает заданный закон движения входного звена, а, следовательно, и всего механизма. Для технологических машин по уравновешивающему (движущему) моменту и частоте вращения входного звена определяется мощность приводного двигателя.
3.2 Силовой расчет
Силовой расчет начинается с последней, т. е. наиболее удаленной от ведущего звена группы Ассура, и кончается расчетом ведущего звена.
В качестве примера рассмотрим силовой расчет двухповодковой групп Ассура. На рис.5,а приведена схема двухповодковой группы второго класса первого вида. На звенья 2 и 3 действуют известные силы и моменты. В точках B и D прикладываем неизвестные реакции R12 и R43 отброшенных звеньев 1 и 4 на оставшиеся 2 и 3, условно направляя их вверх. Уравнение равновесия группы имеет вид
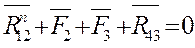
Разложим векторы реакций на составляющие по направлениям звеньев (нормальные) и перпендикулярно звеньям (тангенциальные):
; 
.
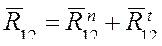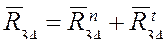Тогда уравнение равновесия примет вид
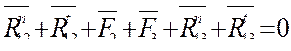
Составляющие реакции 
и 
определяют из условия равновесия звеньев 2 и 3. Для этого составляют уравнения моментов для каждого из звеньев относительно точки C.
Для звена 2
MC( ) + MC( ) + M2 = 0,
откуда
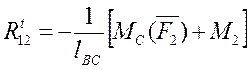
Для звена 3
MC( ) + MC( ) + M3 = 0,
откуда
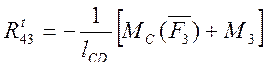
Составляющие реакций 
и 
и полные реакции 
и 
определяем из плана сил (рис.5б), построенного на основе уравнения равновесия.
Из начала плана сил (точка а) в некотором масштабе mF проводим вектор силы 
и из его конца – вектор силы 
.Из начала вектора и из конца вектора проводим найденные выше силы 
^BC и 
^CD. Из точек d и e проводим линии в направлении сил 
^
и 
^. Точка f пересечения этих двух линий определит числовые значения и направления сил
, 
, 
и 
. Полная реакция во внутреннем шарнире C двухповодковой группы определяется из условия равновесия сил, действующих на звенья 2 или 3:
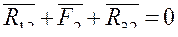
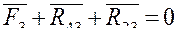
Соединяя точки b и f , найдем реакции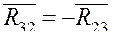 
.
Расчет ведущего (входного) звена. Это звено входит со стойкой во вращательную или поступательную пару пятого класса Кинематическая цепь статически определима при условии 3n -2p5 = 0. Ведущее звено при n = 1 и p5 = 1 не будет находиться в равновесии. Для того чтобы ведущее звено находилось в равновесии, необходимо дополнительно ввести уравновешивающую силу 
или уравновешивающий момент 
, которые бы уравновесили все силы и моменты, приложенные к ведущему звену.
На рис.6 представлены два случая расчета реакции во вращательной паре пятого класса О.
В первом случае (рис.6,а) к ведущему звену приложена уравновешивающая сила Fур, линией действия которой задана. Для ее определения составляем уравнение моментов всех сил, действующих на ведущее звено, относительно точки А:
МГМИМО
Скидка 30% по промокоду Diplom2020
Получи промокод на скидку 20%
Дипломные работы