Синхронизация генераторов, метод хохлова
|
|
(7.39) |
где обозначено
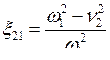 ,
, 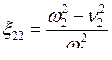 .
.
Левые части уравнений (7.39) описывают вклад энергии в контуры, правые части — потери. Если при A1 = A2 = 0 подкачка энергии больше потерь (это соответствует мягкому режиму возбуждения), то развиваются оба колебания с нормальными частотами w1 и w2. Амплитуда их начинает расти, пока для одного из колебаний (для определённости, на частоте w2) вклад не сравняется с потерями
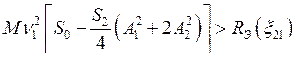 ,
, 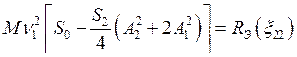 .
.
С этого момента амплитуда A2 перестанет увеличиваться, а A1 будет продолжать расти. Это приведёт к тому, что при расстройке x22 накачка станет меньше потерь и A2 начнёт уменьшаться, что увеличит скорость возрастания A1. В итоге A2 уменьшится до нуля, а A1 возрастёт до такой величины, что будут выполняться соотношения
|
|
(7.40) |
Первое из соотношений (7.40) — условие установления одномодовых колебаний на частоте w1 с амплитудой A1; неравенство показывает, что на частоте w2 подкачка меньше потерь.
Аналогичным образом можно получить условия установления одномодового колебания с частотой w2 и амплитудой A2. Они имеют вид аналогичный (7.40)
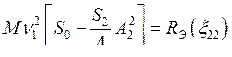 ,
, 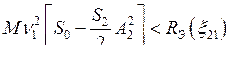 .
.
Простые соображения показывают, что гармонические колебания, описываемые соотношениями (7.40), устойчивы. Пусть, например, амплитуда A1 немного возрастёт, тогда левая часть равенства (7.40) станет меньше правой и A1 вновь уменьшится. Если A1 уменьшится по сравнению со своим стационарным значением, то накачка на этой частоте станет больше потерь и A1 вновь возрастёт. Вместе с тем небольшие изменения A1 слабо сказываются на неравенстве (7.40) и накачка на частоте w2 не сможет превысить потерь. Аналогичные рассуждения доказывают устойчивость колебаний, описываемых последними соотношениями.
Бигармонический режим, описываемый соотношениями (7.39), неустойчив. Действительно, при небольшом увеличении A1 накачка на частоте w2 уменьшается сильнее, чем накачка на частоте w1; это приводит к быстрому уменьшению A2, что увеличивает накачку на частоте w1. Поэтому небольшое увеличение A1 по сравнению со стационарным значением ведёт к резкому уменьшению A2 и росту A1. Система переходит к гармоническим колебаниям с частотой w1. Наоборот, небольшое уменьшение A1 по сравнению со стационарным значением переводит систему в режим гармонических колебаний с частотой w2.
|
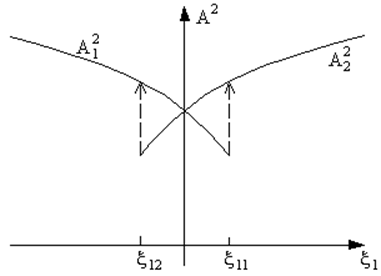
Рис. 73. Зависимость амплитуды генерируемого колебания от расстройки x1 в режиме затягивания. |
Рассмотрим теперь поведение системы в зависимости от изменения парциальной частоты первого контура, т. е. относительно расстройки x1. При частоте n1 << n2 (x1 < 0) в системе существует гармоническое колебание с частотой w1 близкой к n1. При увеличении n1 система входит в область, где возможно существование колебаний как частоты w1, так и частоты w2. Эта область носит название области затягивания частоты. В области затягивания режим генерации зависит от предыстории. Если система вошла в область со стороны x1 < 0 (рис. 71 и 73), то в ней будут существовать колебания с частотой w1 и амплитудой A1. При |
дальнейшем увеличении x1 система при x1 = x11 скачком перейдёт в режим генерации с частотой w2 и амплитудой A2. Если система входит в область затягивания со стороны x1 > 0, то в ней происходят колебания с частотой w2 и амплитудой A2. Переход в режим с частотой w1 и амплитудой A1 наступает при x1 = x12. Расстройки x11 и x12, определяющие границы области затягивания, можно найти из условия нарушения устойчивости соответствующих колебаний.
7.6. Синхронизация генераторов, метод Хохлова
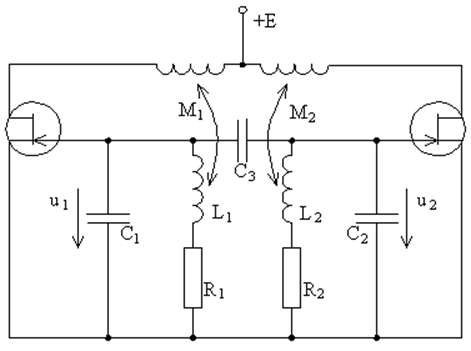
Явление затягивания частоты проявляется и во взаимной синхронизации частот двух связанных генераторов (рис. 74).
|
Рис. 74. Схема двух связанных генераторов. |
В случае двух связанных генераторов с сильно различающимися парциальными частотами генераторы работают практически независимо, и каждый генератор генерирует свою собственную независимую моду со своей нормальной частотой близкой к парциальной. Вблизи синхронизма парциальных частот имеет место взаимная синхронизация генераторов. В полосе синхронизации в системе существуют колебания лишь одной частоты, амплитуда и фаза которых зависят от расстройки парциальных частот и от соотношения мощностей генераторов.
Колебания в связанных генераторах описываются системой приближенных уравнений
|
|
(7.41) |
Здесь n1 и n2 — парциальные частоты контуров; 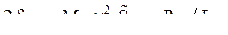 ;
; ![]() — колебательные характеристики первого и второго генераторов; a1, a2 — коэффициенты связи генераторов:
— колебательные характеристики первого и второго генераторов; a1, a2 — коэффициенты связи генераторов:
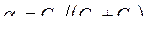 ,
, 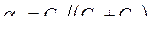 .
.
Будем искать синхронные решения (когда колебания установились с одной частотой), а решать будем с помощью метода ММА, тогда положим
|
|
(7.42) |
где w0 = (n1 + n2)/2. Считая, что a и d малые параметры, запишем укороченные уравнения (3.20) в виде
|
|
(7.43) |
где обозначено F = j — y — разность фаз колебаний генераторов; D1 = w0 — n1, D2 = w0 — n2 — расстройки генераторов;
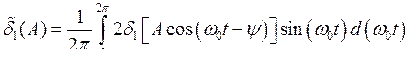 ,
, 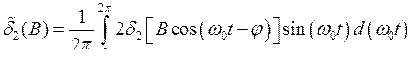 .
.
Вычтем из четвёртого уравнения системы (7.43) второе, тогда получим, что разность фаз F удовлетворяет уравнению:
|
|
(7.44) Рефераты по физике сдают здесь
Другие статьиУзнать стоимость за 15 минут
Распродажа дипломных
Подпишись на наш паблик в ВК
Нужна работа?
|

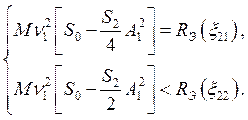
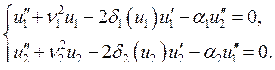
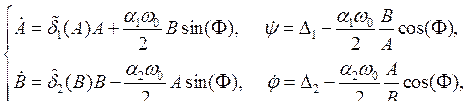
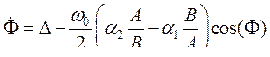 ,
,

