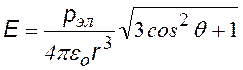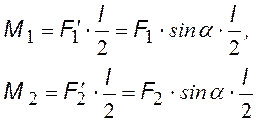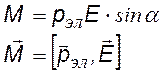Соединения конденсаторов
Соединения конденсаторов.
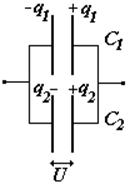
Конденсаторы можно соединять параллельно или последовательно, или смешанным образом: часть параллельно, часть последовательно. При параллельном соединении емкость системы увеличивается и становится равной сумме емкостей. При последовательном соединении емкость системы всегда уменьшается. Последовательное соединение применяют не для уменьшения емкости, а главным образом для уменьшения разности потенциалов на каждом конденсаторе, чтобы не было пробоя конденсатора.
|
|
||
|
|
запишем формулу (§§) для каждого конденсатора и для всей системы (заменив Dj®U); подставляя q в последнюю формулу, получим: С паралл=С1 + С2 Обобщим на случай 3-х и более конденсаторов |
параллельное соединение |
|
|
емкость системы при параллельном соединении конденсаторов (i=1,2,…,n) n — число конденсаторов |
|
|
Заряды на всех обкладках по величине одинаковые. Запишем формулы аналогично предыдущему случаю, произведем те же действия и найдем |
последовательное соединение |
|
|
для 2-х конденсаторов |
|
|
|
емкость системы при последовательном соединении конденсаторов |
|
Электростатика в веществе
Диполь, его поле.
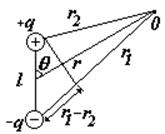
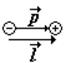
Диполем называется система, состоящая из двух одинаковых по величине, но различных по знаку зарядов q, расположенных на определенном расстоянии l друг от друга. Если это расстояние не меняется, диполь называют жестким. Если расстояние меняется пропорционально напряженности внешнего поля, диполь называют упругим.
Изучение поля диполя и его поведения во внешнем электрическом поле имеет большое значение, так как диполь может служить моделью молекул. На легких частицах, оказавшихся в электрическом поле, возникают индуцированные заряды, и частицы становятся диполями. С помощью достаточно большого количества таких частиц можно наблюдать силовые линии поля, т. к. частички-диполи будут располагаться по силовым линиям поля.
Диполь характеризуют дипольным (электрическим) моментом (см. рис.):
|
|
|
дипольный (электрический) момент диполя – это вектор, проведенный от отрицательного заряда к положительному |
Для определения потенциала j и напряженности Е поля диполя можно воспользоваться принципом суперпозиции:
|
|
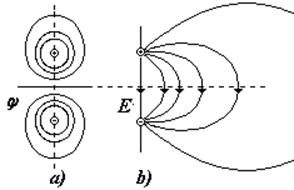
Электростатическое поле диполя имеет сложный вид (см. рис.): a) эквипотенциальные поверхности, b) силовые линии (половина поля) |
|
|
|
||
|
|
Из формулы (©) можно получить потенциал поля диполя для расстояний r, существенно превышающих размер диполя. Для этого в формуле (©) приведем к общему знаменателю, примем r1×r2 » r2, (r1 – r2 ) = l×cos q и введем 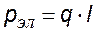 .
.
|
|
потенциал и напряженность поля диполя на больших расстояниях от него |
|
Формулу для Е (без вывода) приводим только для того, чтобы отметить, что и потенциал, и напряженность поля диполя убывают быстрее (j~ 1/ r2 , E ~ 1/r3), чем в случае одиночного заряда (j ~ 1/r, Е~ 1/r2).
Поведение диполя во внешнем электрическом поле.
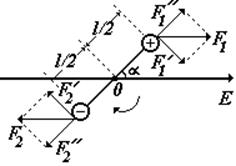 Однородное поле. Внесем диполь в однородное внешнее электрическое поле с напряженностью Е. На заряды диполя будут действовать силы F1 = F2 = qE . Разложим их на составляющие F1¢, F1¢¢ и F2¢, F2¢¢ (см. рис.). Составляющие F1¢¢ и F2¢¢ стремятся растянуть диполь, а составляющие F1¢ и F2¢ создают вращающие моменты и поворачивают диполь (по часовой стрелке) до тех пор, пока он не расположится вдоль силовой линии.
Однородное поле. Внесем диполь в однородное внешнее электрическое поле с напряженностью Е. На заряды диполя будут действовать силы F1 = F2 = qE . Разложим их на составляющие F1¢, F1¢¢ и F2¢, F2¢¢ (см. рис.). Составляющие F1¢¢ и F2¢¢ стремятся растянуть диполь, а составляющие F1¢ и F2¢ создают вращающие моменты и поворачивают диполь (по часовой стрелке) до тех пор, пока он не расположится вдоль силовой линии.
|
|
М1 = М2 – вращающие моменты (моменты сил), векторы моментов направлены от нас ^ чертежу; результирующий момент равен М = М1 + М2= 2qE(l/2)sina. Учитывая, что рэл = ql, получим: |
|
|
вращающий момент (момент сил), действующий на диполь во внешнем поле в скалярной и векторной формах |
Таким образом, в однородном внешнем электрическом поле диполь одновременно будет растягиваться и поворачиваться до тех пор, пока не окажется в положении равновесия, при этом его дипольный момент станет параллельным вектору напряженности внешнего поля.
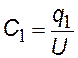
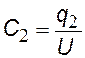
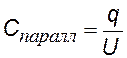
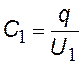
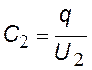
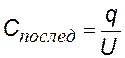
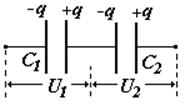
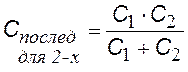
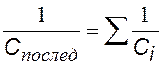
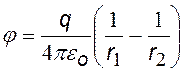 (©)
(©)
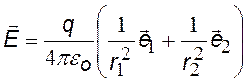
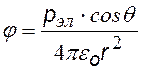 при r >> l
при r >> l