редукция волновой функции
Таким образом, редукция волновой функции ψ заключается в её превращении в новую волновую функцию ![]() :
:
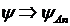 (12.24)
(12.24)
при абсолютно одинаковых условиях измерения.
В исходном состоянии с волновой функцией (12.21) система не обладает конкретным значением физической величины А. Лишь в результате измерения за счет взаимодействия с макроскопическим прибором исследуемая характеристика системы А приобретает конкретное значение ![]() . Иными словами, измерение творит реальность, превращая бесконечный набор потенциальных возможностей системы в единственную реальность, описываемую волновой функцией
. Иными словами, измерение творит реальность, превращая бесконечный набор потенциальных возможностей системы в единственную реальность, описываемую волновой функцией ![]() и её собственным значением
и её собственным значением ![]() . Количественно связь между возможностью и реальностью определяется бесконечной совокупностью вероятностей переходов (12.24)
. Количественно связь между возможностью и реальностью определяется бесконечной совокупностью вероятностей переходов (12.24)
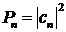 , n=1,2,3,… , (23.25)
, n=1,2,3,… , (23.25)
где величины ![]() удовлетворяет условию (12.9).
удовлетворяет условию (12.9).
Выше отмечалось, что точное без дисперсии измерение физической величины идеальным прибором возможно только в том случае, если система находится в состоянии, описываемом собственной функцией оператора этой физической величины. Если операторы ![]() и
и ![]() двух динамических величин А и В коммутируют, т. е. являются перестановочными для любой волновой функции
двух динамических величин А и В коммутируют, т. е. являются перестановочными для любой волновой функции ![]() в том смысле, что справедливо равенство
в том смысле, что справедливо равенство
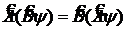 , (12.26)
, (12.26)
то существуют такие состояния системы, которые описываются волновыми функциями ![]() , удовлетворяющими следующим уравнениям:
, удовлетворяющими следующим уравнениям:
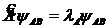
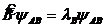 . (12.27)
. (12.27)
Здесь волновая функция ![]() одновременно является собственной функцией сразу двух операторов
одновременно является собственной функцией сразу двух операторов ![]() и
и ![]() .
.
В состоянии, описываемой волновой функцией ![]() , величины А и В имеют точно определенные значения
, величины А и В имеют точно определенные значения ![]() и
и ![]() соответственно, которые могут быть одновременно измерены идеальными приборами без погрешностей. Примерами коммутирующих операторов могут служить следующие пары операторов:
соответственно, которые могут быть одновременно измерены идеальными приборами без погрешностей. Примерами коммутирующих операторов могут служить следующие пары операторов: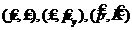 .
.
Если операторы ![]() и
и ![]() не коммутируют и равенство (12.26) не выполняется, то величины А и В не могут быть одновременно точно измеренными, поскольку не существует функций, которые являлись бы собственными функциями сразу двух операторов
не коммутируют и равенство (12.26) не выполняется, то величины А и В не могут быть одновременно точно измеренными, поскольку не существует функций, которые являлись бы собственными функциями сразу двух операторов ![]() и
и ![]() . При одновременном измерении величин А и В идеальными макроскопическими приборами среднеквадратичные отклонения
. При одновременном измерении величин А и В идеальными макроскопическими приборами среднеквадратичные отклонения 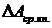 и
и 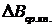 связаны между собой соотношением неопределенностей Гейзенберга (В. Гейзенберг,
связаны между собой соотношением неопределенностей Гейзенберга (В. Гейзенберг,
1927 г.)
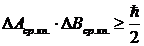 . (12.28)
. (12.28)
Примерами некоммутирующих операторов являются следующие пары операторов: 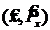 ,
, 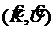 и
и ![]() .
.
Введение коммутирующих и некоммутирующих операторов производится на основе опыта и ведет к глубоким физическим следствиям. В частности, из-за некоммутативности операторов координат и операторов соответствующих проекций импульса на координатные оси нельзя пользоваться понятием траектории частицы. Мы не знаем, как движущаяся частица перемещается из одной точки пространства в другую. Вследствие некоммутативности операторов кинетической энергии ![]() и потенциальной энергии
и потенциальной энергии ![]() можно говорить только о полной энергии частицы.
можно говорить только о полной энергии частицы.
Особое место занимает соотношение неопределенностей для энергии и времени, поскольку для времени в квантовой механике нет оператора и время является точно измеряемой по идеальным часам величиной. Это соотношение неопределенностей имеет вид
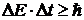 . (12.29)
. (12.29)
Если система находится в стационарном состоянии, то согласно соотношению неопределенностей (12.29) энергию этой системы за время измерения ![]() можно определить лишь с точностью, не превышающей
можно определить лишь с точностью, не превышающей
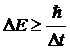 . (12.30)
. (12.30)
Данная неопределенность энергии системы обусловлена взаимодействием этой системы с измерительным прибором и показывает, что для точного измерения энергии стационарного состояния требуется бесконечное время.
Соотношение (12.29) справедливо также для нестационарного состояния, если под ![]() понимать неопределенность энергии нестационарного состояния, а под
понимать неопределенность энергии нестационарного состояния, а под ![]() — характерное время, в течение которого существенно меняется среднее значение физических характеристик этой системы.
— характерное время, в течение которого существенно меняется среднее значение физических характеристик этой системы.
Динамические величины удовлетворяющие соотношению неопределенностей, называются дополнительными. Дополнительные понятия, описывающие состояние объекта наблюдения с разных точек зрения, вместе дают единую картину движения данного объекта. В этом заключается смысл принципа дополнительности Бора, сформулированного им в 1927 г., который устраняет (снимает) противоречие между представлениями дискретности и непрерывности в квантовой механике. Согласно принципу дополнительности для полного описания квантовых явлений необходимо применять два взаимоисключающих (дополнительных) набора классических понятий, совокупность которых дает исчерпывающую информацию об этих явлениях. Классические понятия необходимы в квантовой физике для описания макроскопических условий опытов, создаваемых исследователем с помощью измерительного прибора. Но применение этих классических понятий связано с их «расщеплением» на взаимно исключающие категории. Примерами такого подхода являются корпускулярная и волновая картины, причинно-следственное и пространственно-временное описания, характеристика движения частиц с помощью координат и импульса и т. д.


