Теорема журавского
![]() .
.
При z2 = 0:
![]() ;
;
при z2 = b:
![]()
Таким образом, эпюра поперечной силы постоянна на участках вдоль оси балки (рис. 18д). Знак поперечной силы на втором участке зависит от разности сил ![]() . Эпюра имеет скачки (мгновенное изменение) в местах приложения сил
. Эпюра имеет скачки (мгновенное изменение) в местах приложения сил ![]() ,
, ![]() , .
, .
![]() Эпюра изгибающего момента имеет два характерных линейных участка. На первом участке значение этого фактора возрастает от нуля (в шарнире А) до максимальной величины в месте приложения силы F (точка С), а на втором – линейно убывает до нуля (в шарнире В). С точки зрения прочности опасным является место приложения внешней силы F, так как здесь изгибающий момент достигает максимальной величины и поперечная сила также имеет наибольшее значение.
Эпюра изгибающего момента имеет два характерных линейных участка. На первом участке значение этого фактора возрастает от нуля (в шарнире А) до максимальной величины в месте приложения силы F (точка С), а на втором – линейно убывает до нуля (в шарнире В). С точки зрения прочности опасным является место приложения внешней силы F, так как здесь изгибающий момент достигает максимальной величины и поперечная сила также имеет наибольшее значение.
При рассмотрении правой части отсчёт (![]() ) ведём от точки В влево (рис. 18г). Поперечная сила и изгибающий момент во втором сечении соответственно равны:
) ведём от точки В влево (рис. 18г). Поперечная сила и изгибающий момент во втором сечении соответственно равны:
![]() ;
;
![]() .
.
При ![]() :
: 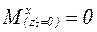 ;
;
при ![]() :
:  .
.
В этом случае эпюры поперечной силы и изгибающего момента имеют тот же вид и значения, что и для левой части балки.
4.3. Теорема Д. И. Журавского
Правильность построения эпюр поперечной силы и изгибающего момента можно проверить при помощи дифференциальных зависимостей Журавского между и распределённой нагрузкой q.
![]() Для вывода этих зависимостей рассмотрим произвольную балку (рис. 19а). Пусть к ней приложены внешние силы F1, F2, …, Fn и распределённая нагрузка q(z), действующая по произвольному закону (положительное направление указано на рис. 19б – вверх). Выделим из бруса элемент длины dz. В пределах длины dz можно считать нагрузку q распределенной равномерно. Слева и справа в поперечных сечениях выделенного элемента приложены положительные силовые факторы Qy, Мх в соответствии с обусловленным выше правилом знаков, отличающиеся на dQy и dMx соответственно.
Для вывода этих зависимостей рассмотрим произвольную балку (рис. 19а). Пусть к ней приложены внешние силы F1, F2, …, Fn и распределённая нагрузка q(z), действующая по произвольному закону (положительное направление указано на рис. 19б – вверх). Выделим из бруса элемент длины dz. В пределах длины dz можно считать нагрузку q распределенной равномерно. Слева и справа в поперечных сечениях выделенного элемента приложены положительные силовые факторы Qy, Мх в соответствии с обусловленным выше правилом знаков, отличающиеся на dQy и dMx соответственно.
Условия равновесия элемента в проекции на ось у даёт
Qy + qdz – Qy – dQy = 0,
или
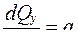 . (4.1)
. (4.1)
Условие равенства нулю моментов всех сил относительно центра тяжести сечения (т. С) приводит к соотношению:
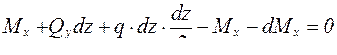 ,
,
откуда, отбрасывая q·dz2/2 , как величину более высокого порядка малости, чем другие слагаемые, имеем
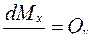 . (4.2)
. (4.2)
Таким образом, поперечная сила Qy есть производная от изгибающего момента Мх по длине бруса, а интенсивность внешней распределённой нагрузки q – в свою очередь, производная от поперечной силы.
Проверим правильность построения эпюр, показанных на рис. 19. Так как в данном случае распределённая нагрузка q=0, то в соответствии с формулой (4.1) поперечные силы на обоих участках постоянны. На участке, где поперечная сила Qy постоянна и положительна, график изгибающего момента Мх, в соответствии с формулой (4.1), линейно возрастает (тангенс угла наклона графика изгибающего момента и есть значение Qy). На участке, где Qy постоянна и отрицательна, эпюра изгибающего момента Mx линейно убывает с тангенсом угла наклона, равным значению Qy на этом участке.
4.4. Нормальные напряжения при изгибе
Для вывода основных расчётных формул рассмотрим частный случай плоского изгиба балки – состояние чистого изгиба. Это состояние деформации наблюдается тогда, когда на каком-то участке балки действует только изгибающий момент Мх, а поперечная сила равна Qy = 0.
Экспериментальные исследования балок при чистом изгибе показывают:
– плоские сечения балки остаются плоскими и после нагружения, испытав лишь некоторый поворот относительно друг друга;
– продольные волокна балки не давят на выше — и нижерасположенные волокна, они либо растянуты, либо сжаты;
– нейтральный слой, перпендикулярный плоскости симметрии балки, отделяет область растянутых волокон от области сжатых волокон.
На рис. 20 представлена схема деформации участка балки при чистом изгибе.
Возьмём на этом участке балки элемент, выделенный двумя сечениями I–I и II–II, находящимися на расстоянии dz друг от друга, и рассмотрим характер его деформации (рис. 20а). При принятом положительном знаке изгибающего момента Мх верхние волокна будут сжаты, а нижние – растянуты (рис. 20б).
Слой волокон, который не деформируется при нагружении, называют нейтральным. Свяжем с ним плоскость xОz.
Кривизна нейтрального слоя в результате поворота поперечных сечений I–I и II–II на угол dθ относительно друг друга равна (рис. 20в):
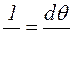 . (4.3)
. (4.3)
Отрезок cd (cd = ab = dz), удалённый от нейтрального слоя вниз на расстояние y, получит приращение длины c′d’−cd, которое можно выразить через кривизну балки:
c′d′ – cd = (ρ + y)dθ – ρdθ=yθ. (4.4)
 Его относительная продольная деформация будет с учётом (4.3) равна:
Его относительная продольная деформация будет с учётом (4.3) равна:
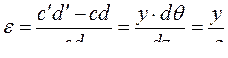 . (4.5)
. (4.5)
Тогда напряжения σ, вызвавшие эту деформацию, будут положительны и по закону Гука при растяжении определяются как
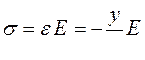 . (4.6)
. (4.6)
Здесь учтено, что для нижней зоны растяжения координата у является отрицательной (рис. 21в).
При чистом изгибе продольная сила N и изгибающий момент относительно оси у–Му отсутствуют (N = 0; Му = 0), но их формальное определение позволяет сделать ряд выводов (рис. 21г):
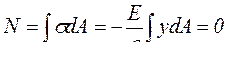 , откуда
, откуда 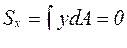 ; (4.7)
; (4.7)
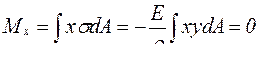 , откуда
, откуда 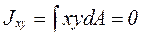 . (4.8)
. (4.8)
Равенство нулю статического момента Sx площади сечения относительно нейтральной линии (оси х) говорит о том, что нейтральная линия проходит через центр тяжести поперечного сечения.
Нулевое значение центробежного момента инерции сечения Jxy означает, что оси х и у являются главными центральными. Следовательно, рассматриваемый вид чистого плоского изгиба реализуется тогда, когда балка деформируется в главной плоскости. Значение изгибающего момента в сечении (с учётом знака момента и положения осей х, у) есть интеграл:


