Теоремы о трёх непараллельных силах
5. Записываем выражение для определения равнодействующей силы в векторном виде:
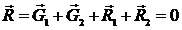
6. Составляем уравнения равновесия в проекциях на выбранные координатные оси:
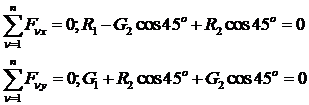
Решаем полученную систему уравнений. Из второго уравнения находим:
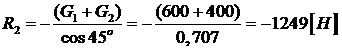
Из первого уравнения получим:
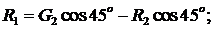
R1= 400∙0,707 – (- 1249)∙0,707 = 1166 ![]()
Ответ:
R1=1166 [H]
R2= -1249 [H]
Знак минус перед численным значением реакции R2 показывает, что стержень ВС не растянут, как предполагалось, а сжат. Действительное направление реакции противоположно направлению, обозначенному на чертеже.
Пример 2
Узел D неподвижно закреплен тремя невесомыми стержнями – АD, ВD и DС. К узлу привязана веревка, растягиваемая грузом ![]() . Крепления стержней шарнирные.
. Крепления стержней шарнирные.
Определить усилия в стержнях, если ОВ=АВ=СЕ=30 см, ВD=40 см.
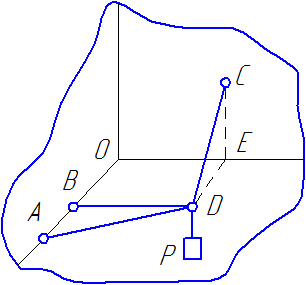
Рисунок 27
Решение:
1. Выбираем объект равновесия.
В качестве объекта равновесия в данной задаче выбираем точку, в которой пересекаются линии действия активной (заданной) силы![]() , а также стержни АD,CD и ВD, поэтому объектом равновесия является узел D.
, а также стержни АD,CD и ВD, поэтому объектом равновесия является узел D.
2. Применяя принцип освобождаемости от связей, заменяем действие на объект равновесия (узел D) мысленно отброшенных связей, которые осуществляются стержнями. Прикладываем вместо стержней реакции стержней ![]()
![]() , и
, и ![]() направляя их вдоль стержня от узла, то есть полагая, что в стержнях действуют растягивающие усилия (рисунок 28).
направляя их вдоль стержня от узла, то есть полагая, что в стержнях действуют растягивающие усилия (рисунок 28).
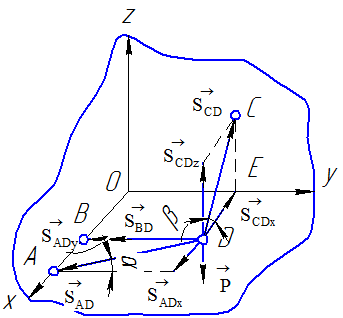
Рисунок 28
3.Выбираем положение системы координат. Начало координат совмещаем с точкой О.
4. Записываем выражение для определения равнодействующей силы в векторном виде:
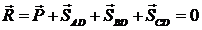 (1)
(1)
5. Стержни AD и CD наклонные, а значит и усилия 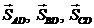 также наклонные, поэтому прежде чем записать уравнения равновесия, запишем проекции на координатные оси.
также наклонные, поэтому прежде чем записать уравнения равновесия, запишем проекции на координатные оси.
Получим:
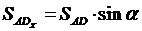 ; (2)
; (2)
; (3)
(4)
(5)
где:
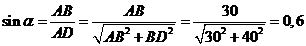 (6)
(6)
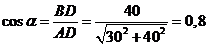 (7)
(7)
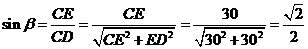 (8)
(8)
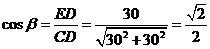 (9)
(9)
Подставив формулы (6-9) в формулы (2-5), получим выражения:
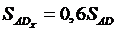 (10)
(10)
(11)
(12)
(13)
6. Составляем уравнения равновесия в проекциях на выбранные координатные оси:
(14)
(15)
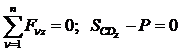 (16)
(16)
Из уравнения (16) определим ![]()
(17)
Из выражения (17), учитывая выражение (13), определим
Из уравнения (14) получим:
(18)
Учитывая выражение (10) и (12), получим:
(19)
Из выражения (19) определяем
(20)
Подставив (20) и (7) в выражение (3), получим:
Из выражения (15) получим:
(21)
Отсюда:
Ответ:
Знак минус перед численным значением усилия в стержне SBD показывает, что стержень ВD не растянут, как предполагалось, а сжат. Действительное направление реакции противоположно направлению, обозначенному на чертеже.
3. Теоремы о трёх непараллельных силах
Теорема 1:
Если плоская система трёх непараллельных сил находится в равновесии, то линии действия этих сил пересекаются в одной точке.
Пусть на тело действует система трех сил ![]() ,
,![]() , и
, и ![]() .
.
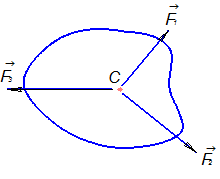
Рисунок 29
На основании следствия из третьей аксиомы силу можно переносить вдоль линии её действия, поэтому систему двух сходящихся сил всегда можно перенести в одну точку — точку пересечения их линии действия.
Рассмотрим сначала две силы ![]() и
и ![]() . По условию теоремы эти силы не параллельны, поэтому существует точка пересечения их линий действия. Складывая эти силы по правилу параллелограмма, получаем силу равнодействующую двух сил
. По условию теоремы эти силы не параллельны, поэтому существует точка пересечения их линий действия. Складывая эти силы по правилу параллелограмма, получаем силу равнодействующую двух сил 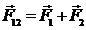 . Теперь вместо трех сил тело находится в равновесии под действием двух сил
. Теперь вместо трех сил тело находится в равновесии под действием двух сил ![]() и
и ![]() (рисунок 30).
(рисунок 30).
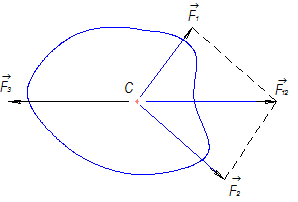
Рисунок 30
По аксиоме о равновесии двух сил в этом случае силы равны по величине и направлены по одной прямой в противоположенные стороны. Следовательно, линия действия силы ![]() проходит через точку С, в которой пересекаются линии действия трех сил, что и требовалось доказать.
проходит через точку С, в которой пересекаются линии действия трех сил, что и требовалось доказать.
Следствие:
Если плоская система трёх непараллельных сил находится в равновесии, то эти силы являются системой трех сходящихся сил.
Рассмотренная теорема используется при решении практических задач.
Одна из заданных сил должна быть задана и по величине и по направлению, направление другой силы (реакции) также должно быть известно. Неизвестными величинами являются величина известной по направлению реакции, а также величина и направление третьей силы (реакции).


