Теплоемкость химически реагирующей термодинамической системы
Для реальных газов показатель к зависит от температуры – к=f(T). Для воздуха и двухатомных газов при 00С показатель к=1,4. С ростом температуры в соответствии с уравнением Майера показатель адиабаты убывает, т. к. теплоемкость ![]() с ростом температуры возрастает:
с ростом температуры возрастает:
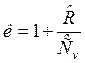 .
.
4.3. Теплоемкость химически реагирующей термодинамической системы
При нагревании смеси газов массой m на один градус необходимо температуру каждого компонента смеси также повысить на один градус. Тогда общая теплоемкость смеси, выраженная через удельные теплоемкости, будет равна:
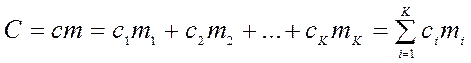 , Дж/К,
, Дж/К,
т. е. 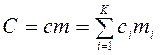 .
.
При этом удельная теплоемкость смеси
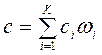 , Дж/кгК,
, Дж/кгК,
где 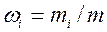 — массовая доля i-го компонента.
— массовая доля i-го компонента.
Общая теплоемкость смеси, выраженная через молярные теплоемкости, будет равна:
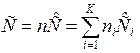 , Дж/К,
, Дж/К,
а молярная теплоемкость смеси газов:
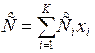 , Дж/мольК,
, Дж/мольК,
где 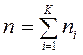 — количество вещества смеси газов, моль;
— количество вещества смеси газов, моль; 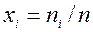 — молярная доля i-го компонента смеси газов.
— молярная доля i-го компонента смеси газов.
Для изобарного ТП (p=const) общая теплоемкость смеси газов равна:
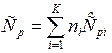 , Дж/К.
, Дж/К.
Полученные ниже формулы справедливы для расчета теплоемкости смесей газов постоянного состава, когда химические реакции не протекают в ТС.
В случае химически реагирующих газовых смесей должны учитываться затраты теплоты на изменение состава смеси, зависящие от температуры. Так для изобарного процесса (p=const) получим:
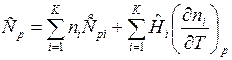 , Дж/К.
, Дж/К.
ГЛАВА 5. Первый закон термодинамики
5.1. Уравнение первого закона термодинамики для сложной открытой системы в общем виде.
В соответствии с законом сохранения и превращения энергии внутренняя энергия изолированной системы (ИС) сохраняется при протекании любых процессов внутри ТС (обратимых и необратимых). При этом энергия может передаваться от одних тел к другим телам лишь внутри ИС с сохранением или изменением формы движения материи.
В термодинамике рассматриваются ТС, которые взаимодействуют с телами окружающей среды, обмениваясь с ними теплотой, различными видами работ и веществом. В этом случае внутренняя энергия ТС будет изменяться. Тогда уравнение первого закона термодинамики для открытой сложной ТС будет иметь вид:
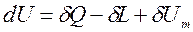 , Дж,
, Дж,
где ![]() — порция подводимой к ТС теплоты
— порция подводимой к ТС теплоты ![]() ;
; ![]() — порция различных видов работ, совершаемых ТС
— порция различных видов работ, совершаемых ТС 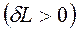 ;
; ![]() — порция внутренней энергии, подводимой в ТС вместе с массой
— порция внутренней энергии, подводимой в ТС вместе с массой ![]() .
.
Таким образом, первый закон термодинамики можно сформулировать так: «Запас внутренней энергии ТС может изменяться за счет подвода теплоты, совершения различных видов работ и массообмена с окружающей средой».
Запас энергии ТС состоит из:
— запаса внутренней энергии, связанной с собственными внутренними свойствами термодинамической системы — ![]() ;
;
— запаса энергии, зависящей от внешних условий. Если на ТС воздействуют внешние силовые поля, то часть полной энергии составит потенциальная энергия. Если ТС, как целое, совершает движение, то в состав полной энергии входит кинетическая энергия ТС.
При рассмотрении открытых систем их потенциальная и кинетическая энергии вводятся в уравнение первого закона термодинамики в виде самостоятельных членов дополнительно к внутренней энергии.
Таким образом, внутренняя энергия ТС – это та часть полного запаса энергии ТС, которая не связана с положением термодинамической системы в поле внешних сил и с ее движением относительно тел окружающей среды и является функцией состояния неподвижной замкнутой системы:
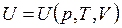 .
.
Дифференциал внутренней энергии ![]() — полный дифференциал. Изменение внутренней энергии в конечном процессе 1-2 определяется состоянием ТС в начале и в конце процесса и не зависит от пути процесса:
— полный дифференциал. Изменение внутренней энергии в конечном процессе 1-2 определяется состоянием ТС в начале и в конце процесса и не зависит от пути процесса:
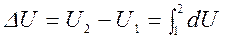 .
.
Порция теплоты ![]() характеризует термическое воздействие. Если внутренняя энергия ТС при этом возрастает, то
характеризует термическое воздействие. Если внутренняя энергия ТС при этом возрастает, то 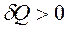 , т. е. порция теплоты считается положительной.
, т. е. порция теплоты считается положительной.
Величина ![]() в уравнении 1-го закона термодинамики характеризует воздействия, называемыми работой, и записывается в виде суммы:
в уравнении 1-го закона термодинамики характеризует воздействия, называемыми работой, и записывается в виде суммы:
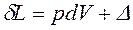 ℒ,
ℒ,
где 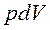 — работа расширения или объемной деформации ТС рассматривается отдельно от прочих видов работ;
— работа расширения или объемной деформации ТС рассматривается отдельно от прочих видов работ; ![]() ℒ — работы немеханического характера и другие виды механической работы за исключением работы расширения.
ℒ — работы немеханического характера и другие виды механической работы за исключением работы расширения.
Если ТС совершает работу над окружающей средой с уменьшением величины внутренней энергии, то работа считается положительной, т. е. ![]() L>0 и
L>0 и ![]() ℒ>0.
ℒ>0.
Для простой (число степеней свободы N=2), закрытой ТС (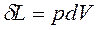 ,
,![]() ℒ=0,
ℒ=0, 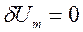 ) уравнение 1-го закона термодинамики имеет вид:
) уравнение 1-го закона термодинамики имеет вид:
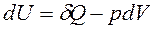 , Дж.
, Дж.
Если ТС представляет собой однородное рабочее тело, свойства которого не изменяются в объеме ТС, то можно использовать удельные величины и записать уравнение 1-го закона термодинамики в виде:
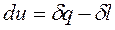 , Дж/кг.
, Дж/кг.
В конечном процессе 1-2 работа расширения равна: 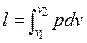 , где
, где 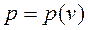 — уравнение процесса. Таким образом, работа расширения – функция процесса и
— уравнение процесса. Таким образом, работа расширения – функция процесса и ![]() — неполный дифференциал. Для кругового процесса (цикла) работа цикла не равна нулю:
— неполный дифференциал. Для кругового процесса (цикла) работа цикла не равна нулю:
![]() ∮
∮![]() ∮
∮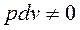 .
.
Для сложных ТС необходимо учитывать другие виды работ (работы немеханического характера и механические работы при деформации других видов, кроме объемной) — ![]() ℒ. При этом элементарная работа любого вида выражается как произведение обобщенной силы Xi на изменение обобщенной координаты dxi:
ℒ. При этом элементарная работа любого вида выражается как произведение обобщенной силы Xi на изменение обобщенной координаты dxi: ![]() ℒ=Xidxi . Например:
ℒ=Xidxi . Например:
— механическая работа при повороте вала машины
ℒМ=МDd,
где MD – крутящий момент на валу; d — элементарный угол поворота вала;
— электрическая работа – работа переноса электрического заряда в электрической цепи:
![]() ℒэл=
ℒэл=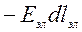 ,
,
где Еэл – напряженность электрического поля; dlэл – количество перенесенного электричества;
— магнитная работа – работа намагничивания магнетика в магнитном поле:
ℒмаг=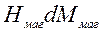 ,
,
где Нмаг – напряженность магнитного поля, Ммаг – магнитный момент.
Теплоту можно выразить через энтропию S. Энтропия S [Дж/К] — функция состояния, введенная в термодинамику Р. Клаузиусом в 1865г., дифференциал которой dS является полным дифференциалом.
Тогда элементарная порция теплоты будет равна:
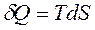 , Дж,
, Дж,
где температура Т играет роль обобщенной силы, а изменение энтропии dS – роль обобщенной координаты.
Удельное количество теплоты
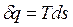 , Дж/кг,
, Дж/кг,
где ds, [Дж/кгК] – удельная энтропия.
Для конечного процесса 1-2 теплота
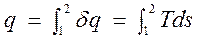 ,
,
где T=T(s) – уравнение процесса.
Количество теплоты q зависит от пути процесса и порция теплоты ![]() не является полным дифференциалом. Для кругового процесса (цикла) теплота цикла не равна нулю
не является полным дифференциалом. Для кругового процесса (цикла) теплота цикла не равна нулю
![]() ∮
∮![]() ∮
∮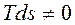 ,
,
И для простой закрытой системы
∮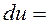 ∮
∮![]() ∮
∮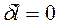 , т. е.
, т. е. 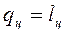 .
.
В открытую ТС вместе с массой ![]() подводится внутренняя энергия и производится работа ввода массы
подводится внутренняя энергия и производится работа ввода массы ![]() , т. е.
, т. е.
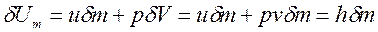 , Дж,
, Дж,
где 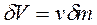 по определению;
по определению; 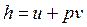 — удельная энтальпия, Дж/кг.
— удельная энтальпия, Дж/кг.
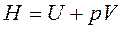 — энтальпия ТС, Дж.
— энтальпия ТС, Дж.
Энтальпия Н – это функция состояния, введенная в термодинамику Гиббсом, и ее дифференциал – полный дифференциал.
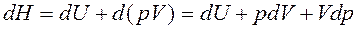 .
.
Энтальпия – это сумма внутренней энергии и работы проталкивания.
Если границу ТС пересекают различные вещества, то 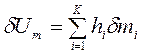 , Дж.
, Дж.
Умножив и разделив это выражение на молярную массу ![]() , кг/моль, получим другое выражение для величины
, кг/моль, получим другое выражение для величины ![]() :
:
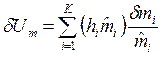 ,
,
где 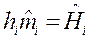 — молярная энтальпия i-го вещества, Дж/моль;
— молярная энтальпия i-го вещества, Дж/моль; 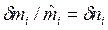 — порция количества вещества i-го компонента.
— порция количества вещества i-го компонента.
Тогда 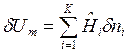 .
.
После подстановки в исходное уравнение 1-го закона термодинамики величин:
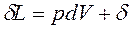 ℒ и
ℒ и 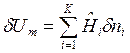 ,
,
получим уравнение 1-го закона термодинамики для сложной открытой ТС в общем виде:
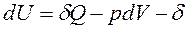 ℒ
ℒ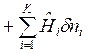 , Дж.
, Дж.
Учитывая, что 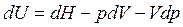 , получим выражение 1-го закона термодинамики через изменение энтальпии:
, получим выражение 1-го закона термодинамики через изменение энтальпии:
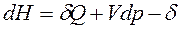 ℒ
ℒ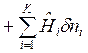 , Дж.
, Дж.
Таким образом, на основании изложенного, можно сделать следующие выводы:


