Термодинамические процессы и их классификация

4.  Плотность – масса единицы объема рабочего тела, или массовая концентрация:

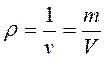, кг/м3.

К параметрам, выражающим интенсивные свойства ТС относятся также напряженности электрического и магнитного полей и др.

Экстенсивными или аддитивными (суммируемыми) называются величины, значения которых пропорциональны количеству вещества ТС. Будем их обозначать прописными (заглавными) буквами. К ним относятся: внутренняя энергия U, энтальпия H, объем V, энтропия S и др. Эти величины называются также полными для m кг ТС.

Если ТС состоит из отдельных частей, то значение экстенсивной величины для ТС равно сумме значений этой величины для всех частей ТС.

Для гомогенной, однородной ТС удобно использовать относительные величины:

1.  Удельные величины, отнесенные к 1 кг вещества. Например: v=V/m – удельный объем, м3/кг; h=H/m – удельная энтальпия, Дж/кг; u=U/m — удельная внутренняя энергия, Дж/кг; s=S/m – удельная энтропия, Дж/кгК и др.

2.  объемные величины, отнесенные к 1м3 вещества: — массовая концентрация, кг/м3 и др.

3.  Молярные величины, отнесенные к 1 молю вещества. Будем обозначать эти величины прописными (заглавными) буквами со знаком «Ù» сверху буквы: — молярный объем, м3/моль, где n – количество вещества, моль; 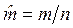— молярная масса, кг/моль; — молярная энтальпия, Дж/моль; — молярная внутренняя энергия, Дж/моль; 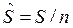— молярная энтропия, Дж/(мольК) и др.

Молем газа называется количество газа, весящего столько граммов, сколько единиц в относительной молекулярной массе М:

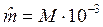кг/моль.

Напомним, что в одном моле любого вещества содержится NА=6,022×1023, моль-1, частиц (молекул) газа, где NA – число (постоянная) Авагадро. В соответствии с законом Авагадро в равных объемах разных газов при одинаковых давлении и температуре содержится равное число молекул. Массы молей разных газов различны, но их молярные объемы при одинаковых физических условиях одинаковы, т. е. не зависят от природы газа.

При t=00C и 1физ. атм 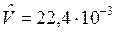м3/моль,

при t=150С и 1техн. атм 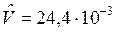м3/моль.

Для характеристики масс частиц вещества будем использовать величины:

1.  Молекулярная масса – масса одной структурной частицы – m1, кг.

2.  Относительная молекулярная масса .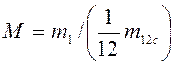
М – величина безразмерная и приводится в таблицах для каждого индивидуального вещества в справочниках.

3.  Молярная масса – масса одного моля данного вещества 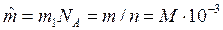, кг/моль, где NA – число Авагадро.

1.5.  Термодинамические процессы и их классификация

Термодинамическим процессом называется изменение состояния ТС в результате ее взаимодействия с окружающей средой. Термодинамические процессы могут быть равновесными и неравновесными.

Непрерывная последовательность равновесных состояний образует равновесный процесс, при котором отсутствуют потери энергии на трение, завихрение, излучение и др., а ТС совершает максимальную работу против внешних сил. Равновесный процесс можно изобразить на координатной плоскости в p-V координатах графически в виде плавно сменяющихся равновесных состояний.

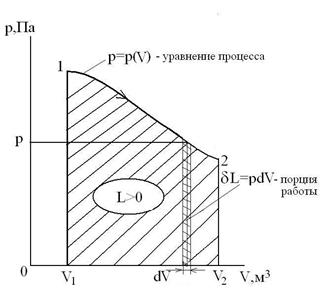
При расширении газа процесс идет с увеличением объема ТС. При этом ТС совершает работу

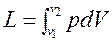, Дж.

Работа расширения положительна (L>0). Процесс, идущий с уменьшением объема ТС, называется процессом сжатия. Работа, затрачиваемая на сжатие газа, отрицательна (L<0).

В термодинамике большое применение получили частные случаи термодинамических процессов: изохорный процесс, протекающий при постоянном объеме (V=const); изобарный процесс, протекающий при постоянном давлении (p=const); изотермический процесс, протекающий при постоянной температуре (T=const) и адиабатный процесс, протекающий без теплообмена ТС с окружающей средой (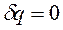 и q=0).

Круговой процесс (цикл) – это процесс, при котором ТС, претерпев ряд изменений, возвращается в исходное состояние.

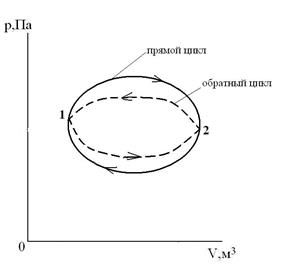
Прямой цикл – цикл тепловых двигателей, идущий в p-V координатах по часовой стрелке (линия расширения лежит выше линии сжатия). Обратный цикл – цикл холодильных установок и машин-орудий, идущий в
p-V координатах против часовой стрелки (линия расширения лежит ниже линии сжатия).

Процессы могут быть обратимыми и необратимыми. При обратимом процессе ТС, пройдя ряд состояний, может вернуться в начальное состояние через те же промежуточные состояния. При этом в ТС и окружающей среде не происходит никаких изменений. При этом процесс является равновесным, т. е. отсутствуют потери энергии на трение, теплообмен и др., а также обеспечивается механическое и термическое равновесие на границе ТС с окружающей средой (обеспечивается бесконечно малая разность давлений и температур в каждый момент процесса).

Все реальные процессы являются неравновесными и необратимыми и могут рассматриваться как равновесные и обратимые только в рамках некоторой идеализации, в рамках определенных допущений.

ГЛАВА 2 УРАВНЕНИЯ СОСТОЯНИЯ ВЕЩЕСТВА

2.1. Термические и калорические уравнения состояния

Общее число термических и калорических уравнений состояния ТС определяется числом ее степеней свободы, т. е. числом воздействующих на ТС обобщенных сил. Эти уравнения устанавливаются опытным путем или находится методами статистической физики.

Для простой ТС (число степеней свободы N=2), на которую действует одна обобщенная сила механического характера – давление р, сопряженная внешнему параметру V, взаимодействие с окружающей средой характеризуется только одним внешним параметром, изменяющимся при данном взаимодействии, (обобщенной координатой) – объемом V и температурой Т (независимый параметр). Тогда равновесные внутренние параметры состояния: давление и внутреннюю энергию U можно выразить в виде функциональных зависимостей: p=p(V,T) – термического уравнения состояния и U=U(V,T) – калорического уравнения состояния.

Термическое уравнение состояния для простой ТС можно представить в виде связи: F(p,V,T)=0. Это уравнение является уравнением термодинамической поверхности или поверхности состояний. Для идеального газа термическим уравнением состояния является уравнение Клапейрона: pV=mRT, где R – удельная газовая постоянная.

Калорическое уравнение состояния идеального газа можно получить из закона Джоуля: «Внутренняя энергия термодинамической системы U при Т=const не зависит от объема V:

.

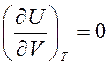Продифференцировав уравнение U=U(V, T), получим:

,

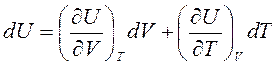где 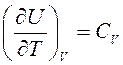— теплоемкость идеального газа в процессе V=const (по определению).

Тогда

,
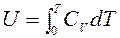