вектор Пойнтинга

В дальней зоне вектор Пойнтинга описывается выражением

, (3.30)

где — угол между радиус-вектором точки наблюдения и осью . Соответствующая интенсивность излучения в направлении точки наблюдения имеет вид

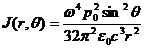. (3.31)

Согласно (3.31) интенсивность излучения диполя не зависит от азимутального угла , определяющего положение меридиональной плоскости.

Все приведенные выше результаты для электромагнитного излучения электрического диполя, совершающего гармонические колебания, получаются путём решения системы уравнений Максвелла.

Средняя за время 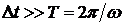мощность излучения диполя определяется следующей формулой

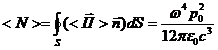. (3.32)

Здесь — замкнутая поверхность, охватывающая диполь. Таким образом, средняя мощность излучения растет пропорционально четвертой степени частоты колебаний диполя. Согласно закону сохранения энергии величина <N> не зависит от выбора замкнутой поверхности S.

С целью наглядного представления распределения интенсивности излучения любого источника по углам наблюдения используется диаграмма направленности. Для построения диаграммы направленности в волновой зоне строится сфера с центром в точке нахождения источника. Через произвольную точку сферы и ее центр проводится прямая. На этой прямой из центра сферы откладывается отрезок, длина которого в заданном масштабе численно равна интенсивности излучения источника в направлении выбранной точки. При мысленном переборе всех точек сферы конец получаемого таким образом отрезка опишет вокруг источника некоторую замкнутую поверхность. Данная поверхность является диаграммой направленности для рассматриваемого источника.

Диаграмма направленности электрического диполя (3.29) строится на основе формулы (3.31) для интенсивности излучения. В плоскости сечение диаграммы направленности в виде "восьмерки" показано на рис.3.4. Для получения полной диаграммы направленности в виде замкнутой поверхности необходимо данную замкнутую кривую повернуть вокруг оси z, вдоль которой ориентирован электрический дипольный момент, на угол . Поверхность, описанная "восьмеркой", и есть диаграмма направленности.

Рис.3.4

Максимальная интенсивность излучения

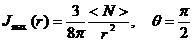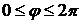, (3.33)

наблюдается в плоскости , перпендикулярной к направлению колебаний электрического диполя. Минимальная интенсивность

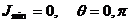(3.34)

соответствует направлению колебаний электрического диполя, то есть вдоль оси z.

При выполнении определенных условий заряженные частицы, движущиеся равномерно в среде с показателем преломления , становятся источником электромагнитного излучения. В 1934г. П. А. Черенков наблюдал такое излучение заряженных частиц, движущихся в среде с постоянной скоростью , превышающей фазовую скорость света 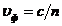в данной среде. Это электромагнитное излучение, получившее название черенковского, заполняет за летящей частицей круговой конус с вершиной в точке нахождения заряженной частицы. Угол полураствора конуса удовлетворяет соотношению

,

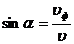где 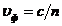— фазовая скорость света в среде и — скорость движения частицы. Черенковское излучение можно рассматривать как электромагнитный аналог звуковой ударной волны, образующейся при движении тела в среде со сверхзвуковой скоростью. Данный эффект используется в черенковских счетчиках заряженных частиц большой энергии.

Переходное излучение наблюдается при пересечении равномерно движущимися заряженными частицами поверхности раздела двух сред с разными показателями преломления. Оно было теоретически предсказано в 1945г. В. Л. Гинзбургом и И. М. Франком. Впервые переходное излучение наблюдалось в 1958г. при прохождении пучка заряженных частиц через границу раздела металл-вакуум.

Кинематические характеристики и акустических и электромагнитных волн зависят от скоростей движения как источника, так и приемника, измеряющего эти характеристики. Зависимость частоты волны от скоростей движения источника и приемника называется эффектом Доплера. К. Доплер в 1842г. теоретически определил эту зависимость для световых и звуковых волн.

Для электромагнитных волн в вакууме эффект Доплера можно рассматривать как преобразование частоты при переходе при переходе из одной инерциальной системы отсчета (ИСО) в другую. Пусть в некоторой ИСО К неподвижный источник излучает электромагнитную волну с частотой и волновым вектором . Частота , измеренная в ИСО , которая движется с постоянной скоростью вдоль оси , согласно преобразованиям Лоренца равна

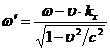, (3.35)

где — проекция волнового вектора на ось . Если система отсчета движется к источнику и , то измеренная частота . Если система отсчета движется от источника и , то измеренная частота . Аналогичные результаты получаются в случае неподвижного приемника и движущегося источника.