ВУЗы по физике
Готовые работы по физике
Как писать работы по физике
Примеры решения задач по физике
Решить задачу по физике онлайнВнутренние силовые факторы при изгибе
11. Что представляют собой осевой и полярный моменты сопротивления сечения?
4. Изгиб
4.1. Общие сведения
Изгибом называется такой вид деформации, при котором при действии внешних сил в поперечных сечениях балки возникает изгибающий момент. Если изгибающий момент в сечении является единственным силовым фактором, изгиб называется чистым. Если в поперечных сечениях стержня наряду с изгибающим моментом действует и поперечная сила, изгиб называется поперечным.
Если плоскость действия изгибающего момента, именуемая силовой плоскостью, проходит через одну из главных центральных осей поперечного сечения балки, то изгиб называют плоским или простым.
Балки являются наиболее часто встречающимися элементами конструкций, воспринимающими нагрузки от других элементов и передающими их опорам.
4.2. Внутренние силовые факторы при изгибе
На первом этапе анализа основная цель заключается в определении и построении эпюр (графиков) внутренних силовых факторов (при плоском изгибе – Qy, Мх) в поперечных сечениях вдоль оси балки для последующего выбора наиболее опасного в прочностном отношении сечения.
Внутренние силовые факторы, действующие в поперечных сечениях балки, определяют (после нахождения реакций опор), используя метод сечений, для чего мысленно рассекают балку на две части и рассматривают равновесие одной из них. Взаимодействие её с другой частью балки заменяют внутренними силовыми факторами: поперечной силой Qy и изгибающим моментом Mx.
Поперечная сила в сечении балки равна алгебраической сумме проекций всех внешних сил, действующих на мысленно отсечённую часть, на ось, перпендикулярную оси балки.
Изгибающий момент в сечении балки равен алгебраической сумме моментов внешних сил, действующих на отсечённую часть, взятых относительно центра тяжести рассматриваемого сечения.
Знаки действия сил и моментов определяют с использованием «правила знаков» (рис. 17).
Замечание:
1. Если сумма внешних сил, лежащих по левую сторону от сечения m−n, даёт равнодействующую, направленную вверх, то поперечная сила в сечении считается положительной, вниз – отрицательной.
Если сумма внешних сил, лежащих по правую сторону от сечения m−n, даёт равнодействующую, направленную вниз, то поперечная сила в сечении положительна, вверх – отрицательна (рис. 17а).
2. Если относительно выбранного сечения m−n изгибающий момент стремится изогнуть балку так, что сжатые волокна сверху, то момент от этого силового фактора положителен, в противном случае – отрицателен (рис. 17б).
Проиллюстрируем определение поперечной силы и изгибающего момента на примере двухопорной балки с грузом G, расчётная модель (схема) которой показана на рис. 18а. К такой модели (расчётной схеме) сводится расчёт конструкций пролётов мостов, валов и осей машин, станков и т. п.
Конструктивно шарнирно-неподвижная опора А не препятствует повороту балки вокруг оси шарнира, но не даёт возможности балке перемещаться вдоль своей оси z и в перпендикулярном направлении – вдоль оси y.
Действие опоры заменяется реакцией FA, направление которой заранее неизвестно. Её раскладывают по направлениям осей y и z: 
и 
.
Шарнирно—подвижная опора В не препятствует свободному повороту балки вокруг оси шарнира и свободному поступательному перемещению вдоль оси z. Поэтому воздействие опоры В заменяется одной вертикальной реакцией . Влияние груза G моделируется сосредоточенной силой F в точке С (рис. 18б).
Опорные реакции (,, ) при плоском изгибе определяют, составляя три уравнения равновесия статики, которые в сопротивлении материалов принято записывать в следующей форме:
– сумма проекций всех сил на ось балки (ось z) равна нулю, в нашем случае это уравнение примет вид:
откуда 
– сумма моментов всех сил относительно опоры А равна нулю:
,
откуда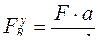 
;
– сумма моментов всех сил относительно опоры В равна нулю:
,
откуда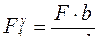 
.
Замечания.
1. Выбор опор А и В за центры приведения объясняется тем, что через опоры проходят линии действия неизвестных реакций и и уравнения получаются проще по виду.
2. В уравнениях моментов условно принято, что момент силы, пытающийся повернуть балку относительно выбранного центра против часовой стрелки, положителен, а по часовой стрелке – отрицателен.
3. Для проверки полученных результатов рекомендуется использовать уравнение – сумма проекций всех сил на вертикальную ось у равна нулю:
,
подставляя в которое полученные выражения для и , получаем тождественное равенство:
.
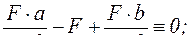
Разобьём балку на два участка, определяемые точками А, С и В приложения сил (рис. 18б). Проведём произвольное сечение I−I на первом участке на расстоянии z1 от опоры А (
). Применим метод РОЗУ. Действие отброшенной (правой) части на оставшуюся (левую) часть заменим силовыми факторами и (рис. 18в). Из условия равновесия оставшейся (левой) части получаем:
– поперечная сила Qy в сечении I−I равна сумме проекций всех внешних сил (активных и реактивных), приложенных к оставшейся части балки:
=.
В данном случае поперечная сила на всём участке постоянна;
– изгибающий момент в сечении I−I равен сумме моментов всех внешних сил, приложенных к оставшейся части балки относительно точки О1 выбранного сечения: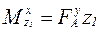 
.
В данном случае изгибающий момент линейно зависит от z.
Используя правило знаков, устанавливаем, что на первом участке поперечная сила и изгибающий момент положительны.
При z1 = 0: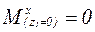 
;
при z1 = a:
.
Для определения внутренних силовых факторов в сечении II-II можно рассматривать левую или правую части (рис. 18г).
При рассмотрении левой части отсчёт z можно вести от точки С, т. е. с конца первого участка (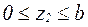
). Тогда поперечная сила и изгибающий момент в этом сечении соответственно равны:
;
МГМИМО
Скидка 30% по промокоду Diplom2020
Получи промокод на скидку 20%
Дипломная