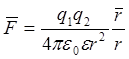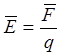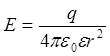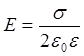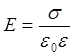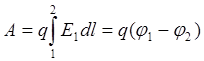Введение в электродинамику

ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ

1. Контрольные работы должны быть представлены до экзаменационной сессии.

2. Номера задач, которые студент должен включить в свою контрольную работу, определяются по таблицам вариантов. Номер варианта равен последней цифре шифра.

3. В контрольной работе нужно привести сведения о студенте по следующему образцу:

4. Условия задач в контрольной работе надо переписать полностью без сокращений. Для замечаний преподавателя на страницах тетради оставлять поля.

5. Если контрольная работа при рецензировании не зачтена, студент обязан представить её на повторную рецензию, включив в неё те задачи, решения которых оказались неверными. Повторную работу необходимо представить вместе с не зачтённой.

6. Зачтённые контрольные работы предъявляются экзаменатору. Студент должен быть готов во время экзамена дать пояснения по существу решения задач, входящих в контрольные работы.

7. Решения задач следует сопровождать краткими, но исчерпывающими пояснениями; в тех случаях, когда возможно, дать чертёж, выполненный с помощью чертёжных принадлежностей.

8. Решать задачу надо в общем виде, т. е. выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи. При таком способе решения не производятся вычисления промежуточных величин.

9. После получения расчётной формулы для проверки правильности её следует подставить в правую часть формулы вместо символов величин обозначения единиц этих величин, произвести с ними необходимые действия и убедиться в том, что полученная при этом единица соответствует искомой величине.

10. Числовые значения величин при подстановке их в расчётную формулу следует выражать только в единицах СИ.

11. При подстановке в расчётную формулу, а также при записи ответа числовые значения величин следует записывать как произведение десятичной дроби с одной значащей цифрой перед запятой на соответствующую степень десяти. Например, вместо 3520 надо записать 3,52×103, вместо 0,00129 записать 1,29×10-3 и т. п.

12 Методика решения задач по физике рекомендует придерживаться следующего алгоритма действий:

1. представление физической модели задачи, т. е. проникновение в физическую суть условий поставленной задачи;

2. поиск решения, т. е. исследование возможных вариантов решения данной задачи;

3. решение задачи, т. е. действия в соответствии с выбранным вариантом;

4. оценка полученных результатов, отказ от нефизических вариантов ответов.

Первый этап решения задачи является наиболее важным. Для адекватного представления физической модели необходимы знания по физике, если их нет, нужно сначала обратиться к теоретическому материалу по соответствующему разделу физики. Поможет в представлении физической сути задачи следующая последовательность действий:

а) внимательно прочитайте условие задачи;

б) запишите ее краткое условие, выполнив перевод внесистемных единиц в систему СИ;

в) при необходимости сделайте чертеж.

На втором этапе после получения физической модели следует применить известные алгоритмы решения аналогичных физических задач. При этом совсем необязательно, что первый же алгоритм приведет к правильному решению. Физические задачи очень разнообразны, для их решения могут использоваться разные алгоритмы. Второй этап называется этапом поиска решения, поэтому, столкнувшись с неудачей, надо искать другие варианты решений. Это нормальный процесс решения задач. При самостоятельном решении задачи необходимо проявить волю и усидчивость.

Успешное выполнение второго этапа предполагает следующую последовательность действий:

а) запишите физические формулы, отражающие законы, которые лежат в основе явлений, описанных в задаче;

б) установите зависимость между исходными данными задачи и искомыми величинами;

в) решите задачу в общем виде, получите буквенное выражение искомых величин;

г) проведите проверку размерности полученных выражений.

На третьем этапе проведите вычисления по полученным формулам.

Четвертый этап заключается в проведении анализа полученного решения.

ЛИТЕРАТУРА

Трофимова Т. И. Курс физики. – М. : Высш. шк., 1985.

Детлаф А. А., Яворский Б. М., Милковская Л. Б. Курс физики. – М. : Высшая школа, 1973 – 1997 – Т. 2.

Зисман Г. А., Тодес О. М. Курс общей физики. – М. : Наука, 1972 – 1974. – Т.2.

Савельев И. В. Курс общей физики. – М. : Наука, 1977 – 1979. – Т. 2.

Калашников С. Г. Электричество. – М. : Наука, 1977.

Сивухин Д. В. Общий курс физики. – М. : Наука, 1977 – 1980. – Т.2.

Матвеев А. Н. Электродинамика. – М. : Высш. шк., 1980.

Сена Л. А. Единицы физических величин и их размерности. – М. : Наука, 1977.

Чертов А. Г. Единицы физических величин. – М. : Высш. шк., 1977.

ПРОГРАММА ПО КУРСУ

«ВВЕДЕНИЕ В ЭЛЕКТРОДИНАМИКУ».

Электростатика

Предмет электростатики. Электрический заряд. Взаимодействие неподвижных зарядов. Закон Кулона. Электростатическое поле. Понятие напряжённости электрического поля как силовой характеристики поля. Напряжённость поля точечного заряда. Принцип суперпозиции электростатических полей. Понятие потока вектора напряжённости электрического поля. Теорема Гаусса для вектора напряжённости электрического поля и её физический смысл. Поле бесконечной плоскости. Работа электрического поля. Понятие потенциала как энергетической характеристики поля. Разность потенциалов. Потенциал поля точечного заряда. Принцип суперпозиции для потенциала. Связь между напряжённостью и потенциалом. Проводники в электростатическом поле. Явление электростатической индукции. Распределение электрического заряда по поверхности проводника. Электрическое поле в полости проводника. Электростатическая защита. Коэффициент ёмкости проводника. Электроёмкость шара. Конденсаторы. Электроёмкость плоского конденсатора. Соединение конденсаторов в батарею Энергия заряженного конденсатора. Диэлектрики в электрическом поле. Явление поляризации диэлектриков. Электрическое поле в диэлектрике.

Постоянный электрический ток

Токи проводимости. Сила тока. Плотность тока. Условия существования тока. Закон Ома в интегральной форме для участка цепи с источником тока и для полной цепи. Понятие электродвижущей силы источника (ЭДС). Понятие напряжения и падения напряжения. Электрическая проводимость и сопротивление проводников. Зависимость сопротивления от температуры. Соединение проводников Основные элементы электрических цепей: источники и приемники электрической энергии, их мощность и К. П.Д.. Баланс мощности. Закон Джоуля – Ленца. Участки схем электрических цепей: ветвь, узел, контур. Потеря напряжения в линиях электропередачи. Расчет электрических цепей с помощью законов Ома и Кирхгофа. Понятие о расчете сложных цепей

Магнитное поле

Магнитное поле электрического тока, силовые линии магнитного поля. Правило буравчика. Напряженность магнитного поля, магнитная индукция, магнитный поток, единицы их измерения. Сила Ампера. Взаимодействие параллельных токов. Сила Лоренца. Движение заряженных частиц в магнитном поле. Действие магнитного поля на проводник с током. Электромагнитная сила. Принцип действия электрического двигателя по­стоянного тока. Явление электромагнитной индукции в замкнутом контуре, катушке, прямолинейном проводнике. Величина и направление ЭДС индукции, правило Ленца, правила левой и правой руки. Потокосцепление. Основной закон электромагнитной индукции. Вихревые токи, их отрицательное действие, способы уменьшения и практическое использование. Явление самоиндукции, величина ЭДС самоиндукции. Ин­дуктивность, единицы ее измерения. Явление взаимоиндукции. Принцип действия трансформатора. Намагничивание ферромагнетиков, кривые первоначального намагничивания. Явление гистерезиса. Магнитная цепь разветвленная и неразветвленная. Понятие о расчете магнитной цепи. Идеальный электрический колебательный контур. Понятие о системе уравнений Максвелла.

Основные формулы

Закон Кулона где q1 и q2 — величины точечных зарядов; ε0 — электрическая постоянная; ε — диэлектрическая проницаемость среды; г-расстояние между зарядами.
Напряженность электрического поля
Напряженность поля:
Точечного заряда
Равномерно заряженной бесконечной плоскости
Между двумя разноименно заряженными бесконечными плоскостями, σ- поверхностная плотность заряда.
Работа перемещения заряда в электростатическом поле где φ1 и φ2 – потенциалы начальной и конечной точек.	Наташа Автор Наташа — контент-маркетолог и блогер, но все это не мешает ей оставаться адекватным человеком. Верит во все цвета радуги и не верит в теорию всемирного заговора. Увлекается «нефрохиромантией» и тайно мечтает воссоздать дома Александрийскую библиотеку. Бесплатное Электронная техника зачет Реакции деления ядра. цепная реакция деления Период полураспада Ядерные силы. модели атомного ядра Ядерная физика формулы Рефераты по физике сдают здесь МГМИМО БГУ ГродноГу Другие статьи Заказ решения задач по физике Решение задач по физике с примерами Подготовка курсовых и дипломных работ по физике Скачать готовые работы по физике Изучение физики в лучших ВУЗах России Ядерная физика формулы Электронная техника зачет Ядерные силы. модели атомного ядра Вопросы по физике атомного ядра и элементарных частиц Реакции деления ядра. цепная реакция деления Период полураспада Пробеги и тормозные способности альфа-частиц в алюминии Основы механики методичка — точность проведения замеров Взаимодействие тяжелых заряженных частиц с веществом Основы механики методичка — погрешности Основы механики методичка Введение в механику сплошной среды Тензор деформации грина Возможные неисправности электромагнитных расходомеров Скорость и ускорение мсс Главные направления и главные деформации Непрерывные отображения мсс Вторая часть билетов по атомной физике Введение в механику сплошной среды — примеры Закон движения сплошной среды Определение резонансных частот колебаний колонны бурильных труб. Интенсивность напряжения Тензор напряжений Вопросы по атомной физике 2015 Элементы робототехники Похожая информация Цепь переменного тока с активным, индуктивным и емкостным сопротивлениями Энергия магнитного поля и расчет индуктивности проводников Индивидуальное задание по гидравлике Дифракция на круглом отверстии и на круглом экране Вращение твердого тела вокруг неподвижной оси Закон ома в интегральной форме Основы гидростатики Электрические сети строительных площадок Устройство синхронного генератора Распродажа дипломных Скидка 30% по промокоду Diplom2020 Подпишись на наш паблик в ВК Получи промокод на скидку 20% Нужна работа?  Заказ дипломных работ у наших партнеров